Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Jesus knew their thoughts and said to them, “Every kingdom divided against itself will be ruined, and every city or household divided against itself will not stand.” Matthew‬ ‭12‬:‭25‬ ‭NIV‬‬‬‬‬

7-05 Rotated Conics

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.6.7

Note: This assignment is long and should take two days.

sun dial declination
Figure 1: Chinook Trail Monumental Sundial with a declination line. credit (flickr/John Carmichael)

The declination line on the sundial in Figure 1 is not horizontal or vertical. It is rotated. This lesson will explore rotated conics and their equations.

Rotated Conics

All the conics in the previous lessons were in the form Ax2 + Cy2 + Dx + Ey + F = 0. All these conics are either horizontal or vertical. Conics that are not horizontal or vertical require using the missing B term. The general form of conics becomes Ax2 + Bxy + Cy2 + Dx + Ey + F = 0.

The Bxy term prevents completing the square to write the conics in standard form. In order to graph these rotated conics or write them in standard form, the Bxy term needs to be eliminated. Then write the equation in the form A′(x′)2 + C′(y′)2 + D′x′ + E′y′ + F′ = 0 by rotating the coordinate axes counterclockwise through the angle θ, where

$$\cot ⁡2θ = \frac{A - C}{B}$$

where 0 < 2θ < π and 0 < θ < \(\frac{π}{2}\).

The coefficients of the new equation are obtained by making the substitutions

$$\begin{alignat}{2}x &= x′ \cos θ &- y′\sin θ\\ y &= x′ \sin θ &+ y′ \cos θ\end{alignat}$$

Invariants Under Rotation

The following quantities to not change during rotations.

The invariants can be used to classify conics without eliminating the Bxy term. B2 – 4AC is the discriminant and identifies the type of conic.

Classify Rotated Conics

If the conic is in the form Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and B ≠ 0, then conic can be classified by

Writing Rotated Conics in Standard Form

Given a conic written as Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 where B ≠ 0

  1. Find the angle of rotation using

    $$\cot 2θ = \frac{A - C}{B}$$

    where 0 < θ < \(\frac{π}{2}\).

  2. Find sin θ and cos θ.

    If θ is a special angle, evaluate sin θ and cos θ directly.

    If θ is not a special angle,

    1. Find cot 2θ.
    2. Reciprocal to find tan 2θ.
    3. Use 1 + tan2 u = sec2 u to find sec 2θ. (If tan 2θ < 0, then sec 2θ < 0.)
    4. Reciprocal to find cos 2θ.

    5. Use the half-angle formulas to find sin θ and cos θ.

      $$\sin θ = \sqrt{\frac{1 - \cos 2θ}{2}} \text{ and } \cos θ = \sqrt{\frac{1 + \cos 2θ}{2}}$$

  3. Find the substitutions for x and y using

    $$\begin{alignat}{2}x &= x′ \cos θ &&- y′ \sin θ\\y &= x′ \sin θ &&+ y′ \cos θ\end{alignat}$$

  4. Make the substitutions and arrange the terms into standard form.
Graph a Rotated Conic
  1. Draw the rotated axes.
  2. Using the rotated axes, sketch the conic.

Example 1: Write a Rotated Conic in Standard Form

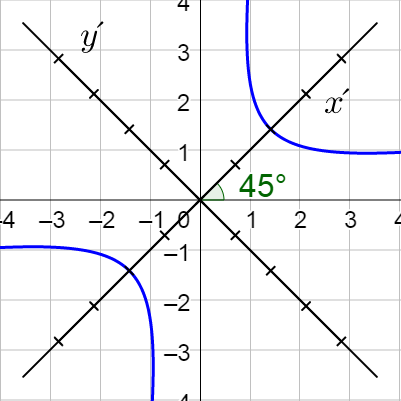
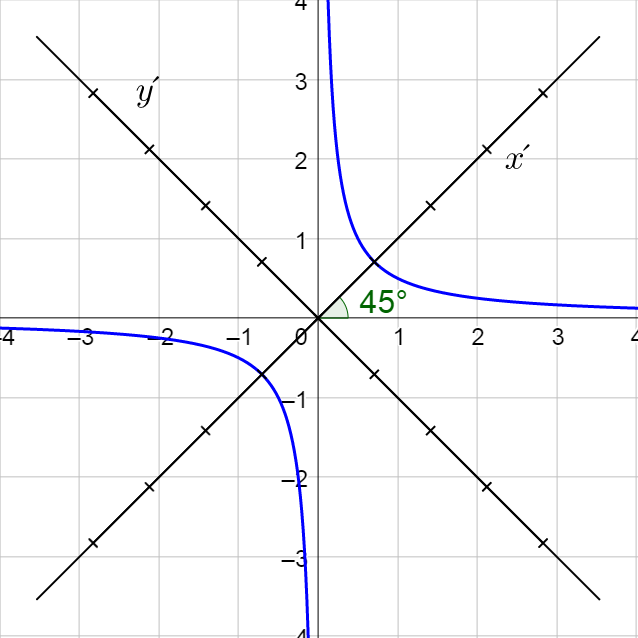
Classify \(xy = \frac{1}{2}\) and then write it in standard form.

Solution

Compare \(xy = \frac{1}{2}\) to Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and find that A = 0, B = 1, and C = 0.

Classify the conic by using the discriminant.

B2 − 4AC

12 – 4(0)(0) = 1

Since B2 − 4AC > 0, it is a hyperbola.

Write it in standard form by first finding the angle of rotation.

$$\cot ⁡2θ = \frac{A - C}{B} = \frac{0}{1} = 0$$

$$2θ = \frac{π}{2}$$

$$θ = \frac{π}{4}$$

Find the substitutions for x and y.

$$\begin{alignat}{2}x &= x′ \cos \frac{π}{4} &- y′ \sin \frac{π}{4}\\ y &= x′ \sin \frac{π}{4} &+ y′ \cos \frac {π}{4}\end{alignat}$$

$$\begin{alignat}{2}x &= \frac{\sqrt{2}}{2} x′ &- \frac{\sqrt{2}}{2} y′\\ y &= \frac{\sqrt{2}}{2} x′ &+ \frac{\sqrt{2}}{2} y′\end{alignat}$$

Substitute these into the original equation and simplify.

$$xy = \frac{1}{2}$$

$$\left(\frac{\sqrt{2}}{2} x′ - \frac{\sqrt{2}}{2} y′\right)\left(\frac{\sqrt{2}}{2} x′ + \frac{\sqrt{2}}{2} y′\right) = \frac{1}{2}$$

$$\frac{1}{2} (x′)^2 - \frac{1}{2} (x′y′) + \frac{1}{2} (x′y′) - \frac{1}{2} (y′)^2 = \frac{1}{2}$$

$$(x′)^2 - (y′)^2 = 1$$

From the equation, this conic is a hyperbola.

Figure 2: \(xy = \frac{1}{2}\) is \((x′)^2 - (y′)^2 = 1\) rotated \(\frac{π}{4}\) radians.
Try It 1

Classify \(xy - 2 = 0\) and then write the conic in standard form.

Answer

Hyperbola; \(\frac{(x′)^2}{4}-\frac{(y′)^2}{4} = 1\)

Example 2: Graph a Rotated Conic

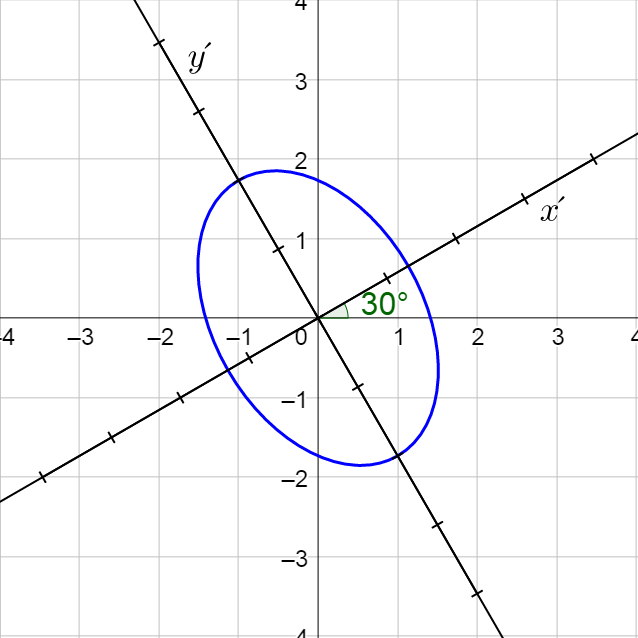
Classify \(3x^2 + \sqrt{3}xy + 2y^2 - 6 = 0\) and then sketch the graph.

Solution

Compare \(3x^2 + \sqrt{3}xy + 2y^2 - 6 = 0\) to Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and find that A = 3, B = \(\sqrt{3}\), and C = 2.

Classify the conic by using the discriminant.

B2 − 4AC

$$\left(\sqrt{3}\right)^2 - 4(3)(2) = -21$$

Since B2 − 4AC < 0, it is a ellipse.

Write it in standard form by first finding the angle of rotation.

$$\cot ⁡2θ = \frac{A - C}{B} = \frac{3 - 2}{\sqrt{3}} = \frac{1}{\sqrt{3}}$$

$$2θ = \frac{π}{3}$$

$$θ = \frac{π}{6}$$

Find the substitutions for x and y.

$$\begin{alignat}{2}x &= x′ \cos \frac{π}{6} &&- y′ \sin \frac{π}{6}\\ y &= x′ \sin \frac{π}{6} &&+ y′ \cos \frac{π}{6}\end{alignat}$$

$$\begin{alignat}{2}x &= \frac{\sqrt{3}}{2} x′ &&- \frac{1}{2} y′\\ y &= \frac{1}{2} x′ &&+ \frac{\sqrt{3}}{2} y′\end{alignat}$$

Substitute these into the original equation and simplify.

$$3\left(\frac{\sqrt{3}}{2} x′ - \frac{1}{2} y′\right)^2 + \sqrt{3} \left(\frac{\sqrt{3}}{2} x′ - \frac{1}{2} y′\right)\left(\frac{1}{2} x′ + \frac{\sqrt{3}}{2} y′\right) + 2\left(\frac{1}{2} x′ + \frac{\sqrt{3}}{2} y′\right)^2 - 6 = 0$$

$$3\left(\frac{3}{4} (x′)^2 - \frac{\sqrt{3}}{2} x′y′ + \frac{1}{4} (y′)^2\right) + \sqrt{3}\left(\frac{\sqrt{3}}{4} (x′)^2 + \frac{1}{2} x′y′ - \frac{\sqrt{3}}{4} (y′)^2\right) + 2\left(\frac{1}{4} (x′)^2 + \frac{\sqrt{3}}{2} x′y′ + \frac{3}{4} (y′)^2\right) - 6 = 0$$

$$\frac{9}{4} (x′)^2 - \frac{3\sqrt{3}}{2} x′y′ + \frac{3}{4} (y′)^2 + \frac{3}{4} (x′)^2 + \frac{\sqrt{3}}{2} x′y′ - \frac{3}{4} (y′)^2 + \frac{1}{2} (x′)^2 + \sqrt{3} x′y′ + \frac{3}{2} (y′)^2 - 6 = 0$$

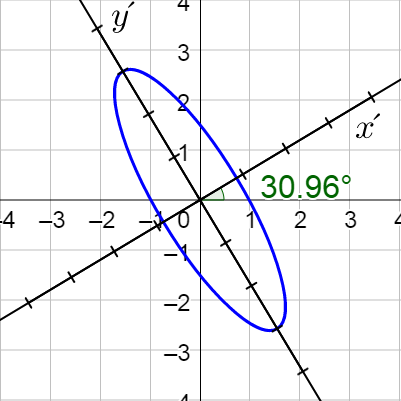
$$\frac{7}{2} (x′)^2 + \frac{3}{2} (y′)^2 = 6$$

Divide by 6 to write to make the equation equal 1.

$$\frac{(x′)^2}{^{12}/_7} + \frac{(y′)^2}{4} = 1$$

Thus it is a vertical ellipse with a = 2 and b = \(\frac{2\sqrt{21}}{7}\) and center (0, 0).

Draw the rotated axis, then move a = 2 along the rotated y-axis and b = \(\frac{2\sqrt{21}}{7}\) along the rotated x-axis.

Connect the points with a nice ellipse.

Figure 3: \(3x^2 + \sqrt{3}xy + 2y^2 - 6 = 0\).
Try It 2

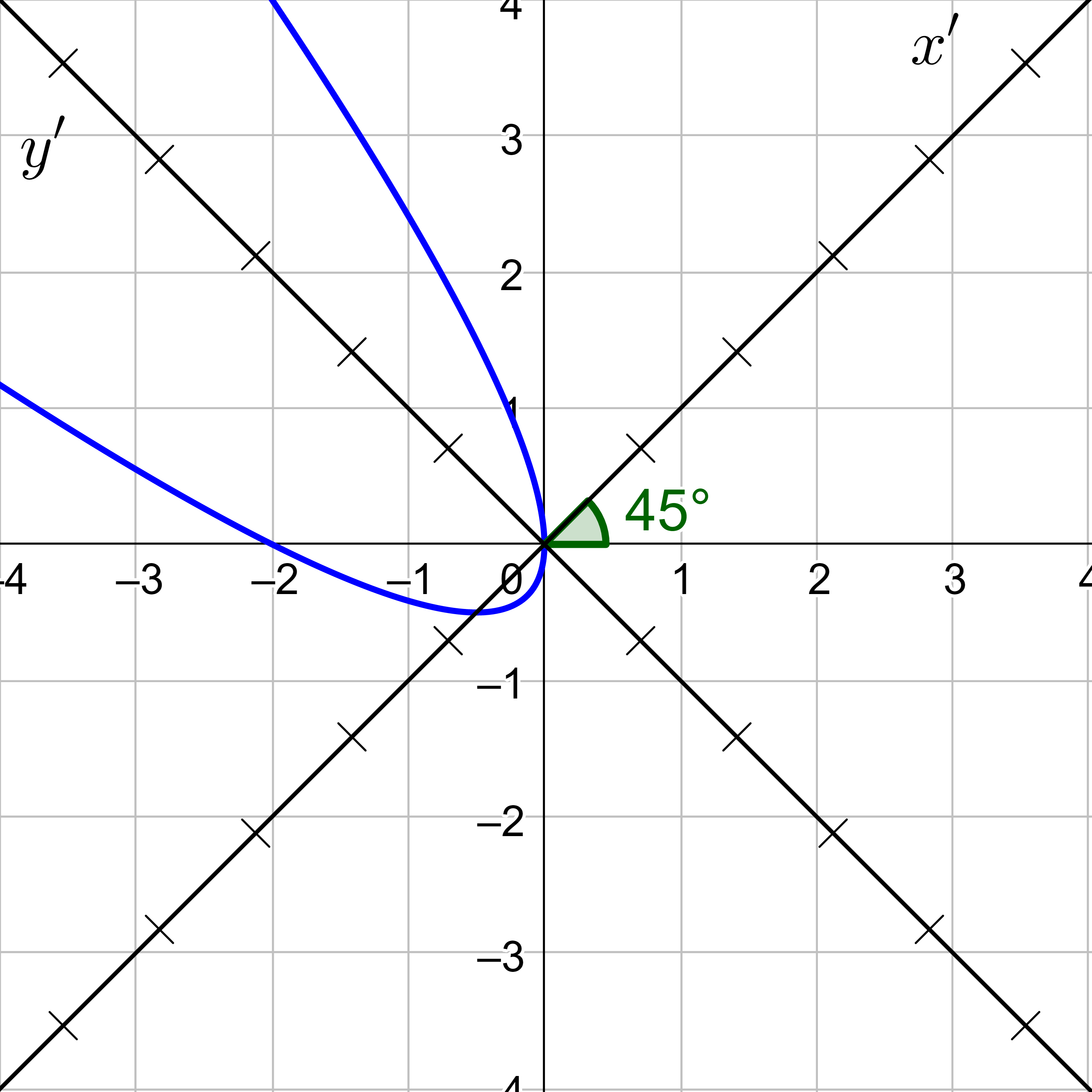
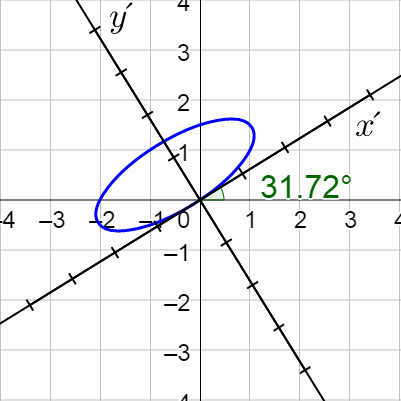
Classify 5x2 − 6xy + 5y2 − 32 = 0 and then sketch its graph.

Answer

Ellipse; \(\frac{(x′)^2}{16} + \frac{(y′)^2}{4} = 1\);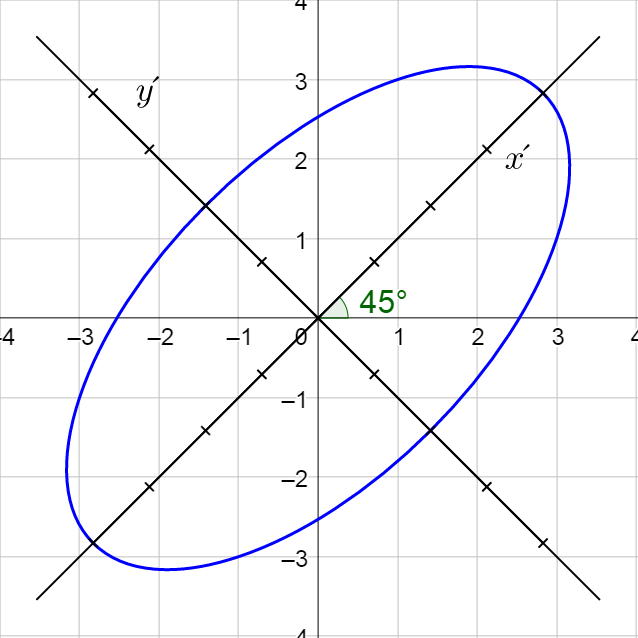

Example 3: Graph a Rotated Conic

Classify \(3x^2 - 2\sqrt{3} xy + y^2 - 16x - 16\sqrt{3} y = 0\) and then sketch the graph.

Solution

Compare \(3x^2 - 2\sqrt{3} xy + y^2 - 16x - 16\sqrt{3} y = 0\) to Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and find that A = 3, B = \(-2\sqrt{3}\), and C = 1.

Classify the conic by using the discriminant.

B2 − 4AC

$$\left(-2\sqrt{3}\right)^2 – 4(3)(1) = 0$$

Since B2 − 4AC = 0, it is a parabola.

Write it in standard form by first finding the angle of rotation.

$$\cot ⁡2θ = \frac{A - C}{B} = \frac{3 - 1}{-2\sqrt{3}} = -\frac{1}{\sqrt{3}}$$

$$2θ = \frac{2π}{3}$$

$$θ = \frac{π}{3}$$

Find the substitutions for x and y.

$$\begin{alignat}{2}x &= x′ \cos \frac{π}{3} &&- y′ \sin \frac{π}{3}\\ y &= x′ \sin \frac{π}{3} &&+ y′ \cos \frac{π}{3}\end{alignat}$$

$$\begin{alignat}{2}x &= \frac{1}{2} x′ &&- \frac{\sqrt{3}}{2} y′\\ y &= \frac{\sqrt{3}}{2} x′ &&+ \frac{1}{2} y′\end{alignat}$$

Substitute these into the original equation and simplify.

$$3\left(\frac{1}{2} x′ - \frac{\sqrt{3}}{2} y′\right)^2 - 2\sqrt{3}\left(\frac{1}{2} x′ - \frac{\sqrt{3}}{2} y′\right)\left(\frac{\sqrt{3}}{2} x′ + \frac{1}{2} y′\right) + \left(\frac{\sqrt{3}}{2} x′ + \frac{1}{2} y′\right)^2 - 16\left(\frac{1}{2} x′ - \frac{\sqrt{3}}{2} y′\right) - 16\sqrt{3} \left(\frac{\sqrt{3}}{2} x′ + \frac{1}{2} y′\right) = 0$$

$$3\left(\frac{1}{4} (x′)^2 - \frac{\sqrt{3}}{2} x′y′ + \frac{3}{4} (y′)^2\right) - 2\sqrt{3} \left(\frac{\sqrt{3}}{4} (x′)^2 - \frac{1}{2} x′y′ - \frac{\sqrt{3}}{4} (y′)^2\right) + \left(\frac{3}{4} (x′)^2 + \frac{\sqrt{3}}{2} x′y′ + \frac{1}{4} (y′)^2\right) - 16\left(\frac{1}{2} x′ - \frac{\sqrt{3}}{2} y′\right) - 16\sqrt{3} \left(\frac{\sqrt{3}}{2} x′ + \frac{1}{2} y′\right) = 0$$

$$\frac{3}{4} (x′)^2 - \frac{3\sqrt{3}}{2} x′y′ + \frac{9}{4} (y′)^2 - \frac{3}{2} (x′)^2 + \sqrt{3} x′y′ + \frac{3}{2} (y′)^2 + \frac{3}{4} (x′)^2 + \frac{\sqrt{3}}{2} x′y′ + \frac{1}{4} (y′)^2 - 8 x′ + 8\sqrt{3} y′ - 24 x′ - 8\sqrt{3} y′ = 0$$

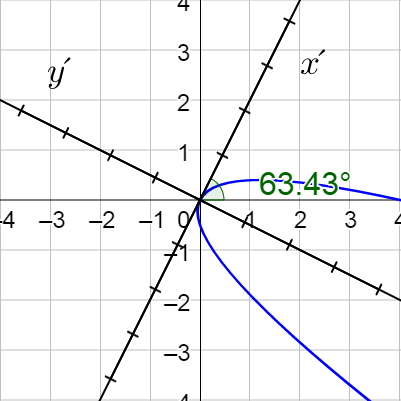
$$4 (y′)^2 - 32 x′ = 0$$

$$(y′)^2 = 8x′$$

This is a horizontal parabola. Graph it by drawing the rotated axes and plotting points.

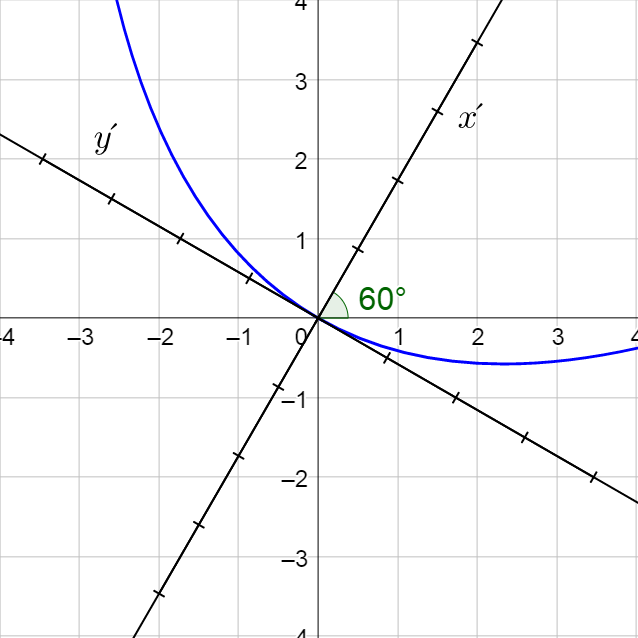
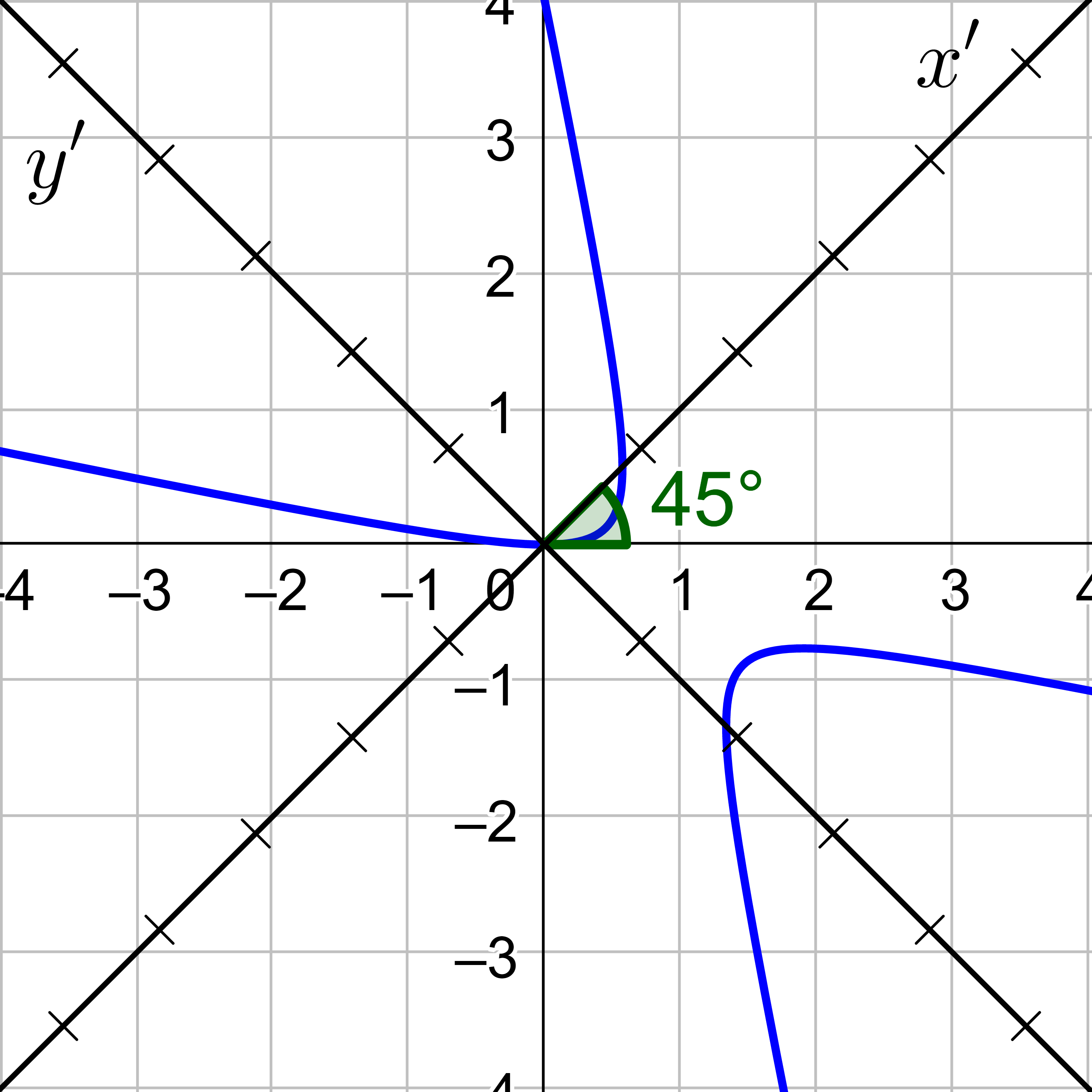
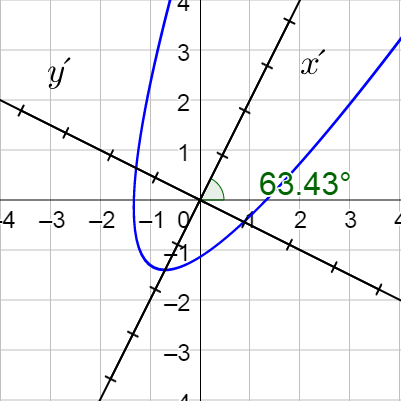
Figure 4: \(3x^2 - 2\sqrt{3} xy + y^2 - 16x - 16\sqrt{3} y = 0\).
Try It 3

Classify \(3x^2 + 2\sqrt{3}xy + y^2 + 8x - 8\sqrt{3}y = 0\) and then sketch the graph.

Answer

Parabola; (x′)2 = 4y′;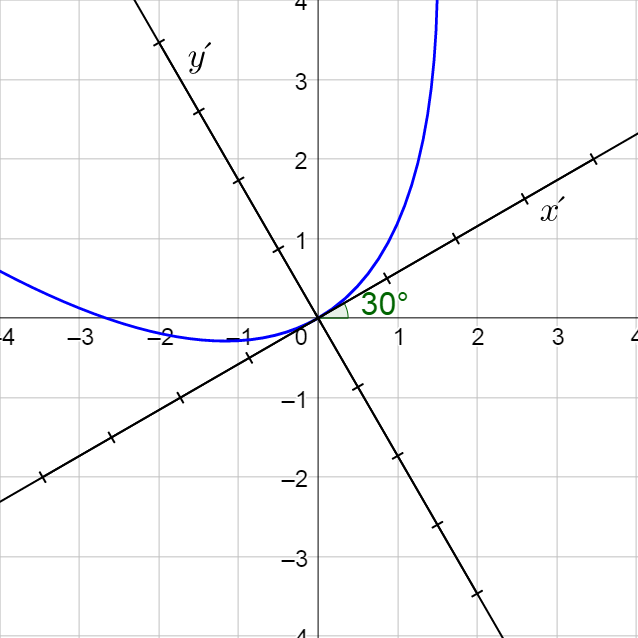

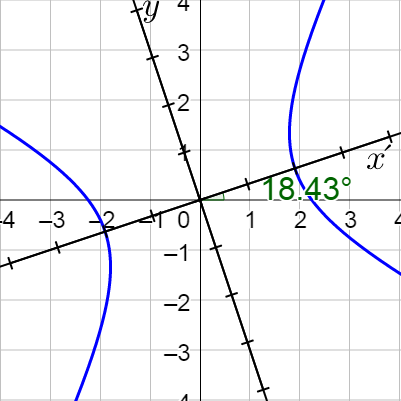
Example 4: Graph a Rotated Conic without a Special Angle of Rotation

Classify 5x2 + 4xy + 2y2 − 16 = 0 and then sketch the graph.

Solution

Compare 5x2 + 4xy + 2y2 − 16 = 0 to Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and find that A = 5, B = 4, and C = 2.

Classify the conic by using the discriminant.

B2 − 4AC

42 – 4(5)(2) = -24

Since B2 − 4AC < 0, it is a ellipse.

Write it in standard form by first finding the angle of rotation.

$$\cot ⁡2θ = \frac{A - C}{B} = \frac{5 - 2}{4} = \frac{3}{4}$$

$$2θ = 53.13°$$

$$θ = 26.57°$$

This is not on the unit circle, so it will not produce a special angle. So the substitutions for x and y are usually found by using half-angle formulas to find sin θ and cos θ.

  1. Find cot 2θ.

    $$\cot ⁡2θ = \frac{3}{4}$$

  2. Reciprocal to find tan 2θ.

    $$\tan ⁡2θ = \frac{4}{3}$$

  3. Use 1 + tan2 u = sec2 u to find sec 2θ. (If tan 2θ < 0, then sec 2θ < 0.)

    $$1 + \tan^2 2θ = \sec^2 2θ$$

    $$1 + \left(\frac{4}{3}\right)^2 = \sec^2 2θ$$

    $$1 + \frac{16}{9} = \sec^2 2θ$$

    $$\frac{25}{9} = \sec^2 2θ$$

    $$\sec 2θ = \frac{5}{3}$$

  4. Reciprocal to find cos 2θ.

    $$\cos 2θ = \frac{3}{5}$$

  5. Use the half-angle formulas to find sin θ and cos θ.

    $$\sin θ = \sqrt{\frac{1 - \cos 2θ}{2}} \text{ and } \cos θ = \sqrt{\frac{1 + \cos 2θ}{2}}$$

    $$\sin θ = \sqrt{\frac{1 - ^3/_5}{2}} \text{ and } \cos θ = \sqrt{\frac{1 + ^3/_5}{2}}$$

    $$\sin θ = \sqrt{\frac{^2/_5}{2}} \text{ and } \cos θ = \sqrt{\frac{^8/_5}{2}}$$

    $$\sin θ = \sqrt{\frac{1}{5}} \text{ and } \cos θ = \sqrt{\frac{4}{5}}$$

    $$\sin θ = \frac{\sqrt{5}}{5} \text{ and } \cos θ = \frac{2\sqrt{5}}{5}$$

Substitute these into the original equation and simplify.

$$5\left(\frac{2\sqrt{5}}{5} x′ - \frac{\sqrt{5}}{5} y′\right)^2 + 4 \left(\frac{2\sqrt{5}}{5} x′ - \frac{\sqrt{5}}{5} y′\right)\left(\frac{\sqrt{5}}{5} x′ + \frac{2\sqrt{5}}{5} y′\right) + 2\left(\frac{\sqrt{5}}{5} x′ + \frac{2\sqrt{5}}{5} y′\right)^2 - 16 = 0$$

$$5\left(\frac{4}{5} (x′)^2 - \frac{4}{5} x′y′ + \frac{1}{5} (y′)^2\right) + 4\left(\frac{2}{5} (x′)^2 + \frac{3}{5} x′y′ - \frac{2}{5} (y′)^2\right) + 2\left(\frac{1}{5} (x′)^2 + \frac{4}{5} x′y′ + \frac{4}{5} (y′)^2\right) - 16 = 0$$

$$4(x′)^2 - 4x′y′ + (y′)^2 + \frac{8}{5} (x′)^2 + \frac{12}{5} x′y′ - \frac{8}{5} (y′)^2 + \frac{2}{5} (x′)^2 + \frac{8}{5} x′y′ + \frac{8}{5} (y′)^2 - 16 = 0$$

$$6(x′)^2 + (y′)^2 = 16$$

Divide by 16 to write to make the equation equal 1.

$$\frac{3(x′)^2}{8} + \frac{(y′)^2}{16} = 1$$

Thus, it is a vertical ellipse with a = 4 and b = \(\frac{2\sqrt{6}}{3}\) and center (0, 0).

Draw the rotated axis, then move a = 4 along the rotated y-axis and b = \(\frac{2\sqrt{6}}{3}\) along the rotated x-axis.

Connect the points with a nice ellipse.

Figure 5: 5x2 + 4xy + 2y2 − 16 = 0
Try It 4

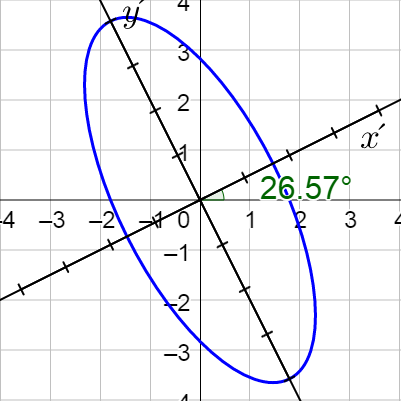
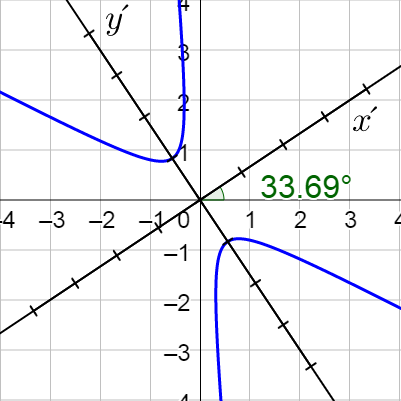
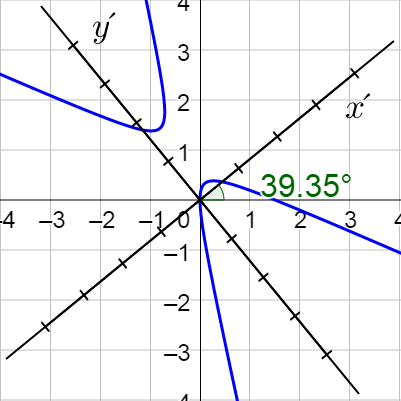
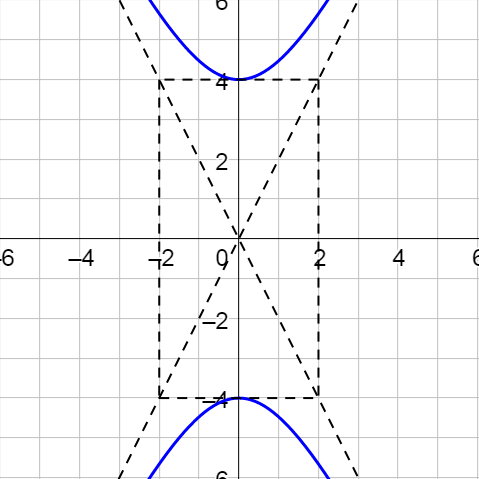
Classify 7x2 + 5xy – 7y2 – 30 = 0 and the sketch its graph.

Answer

Hyperbola;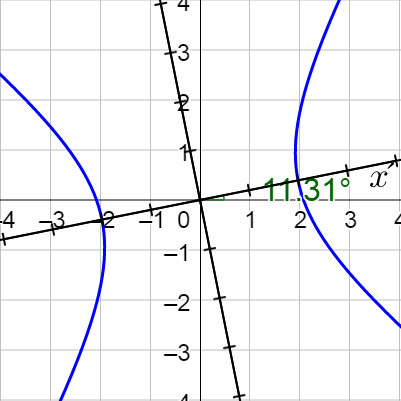

Using a Graphing Utility

Graph a Rotated Conic on a Graphing Calculator
  1. Arrange the terms in descending powers of y.
  2. Group the terms by the powers of y. Factor the y2 and factor the y.
  3. Fill in the quadratic formula, \(y = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}\), where a is the expression multiplied with the y2, b is the expression multiplied with the y, and c is the expression without a y.
  4. Because of the ±, two equations will have to be entered into the calculator; one just + and the other just −.

Example 5: Classify Conics

For each of the following, classify the graph, use the quadratic formula to solve for y, and use a graphing utility to graph the equation.

  1. x2 + 6xy − 2y2 + 3x = 0
  2. 2x2 – 2xy + y2 – 2y = 0
  3. 4x2 − 4xy + y2 − x + y = 0
Solution

  1. Classify the graph using the discriminant. B2 – 4AC = 62 – 4(1)(−2) = 44 > 0, so it is a hyperbola.

    To solve for y, rearrange terms in powers of y and factor.

    $$x^2 + 6xy - 2y^2 + 3x = 0$$

    $$-2y^2 + 6xy + (x^2 +3x) = 0$$

    Now fill in the quadratic formula: \(y = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}\).

    $$y = \frac{-6x ± \sqrt{(6x)^2 - 4(-2)(x^2 + 3x)}}{2(3)}$$

    Because of the ± sign, you will have to input two equations, one with + and one with −, to make the graph. Notice that the graph is shifted and (0, 0) is not the center.

    Figure 6: x2 + 6xy − 2y2 + 3x = 0.

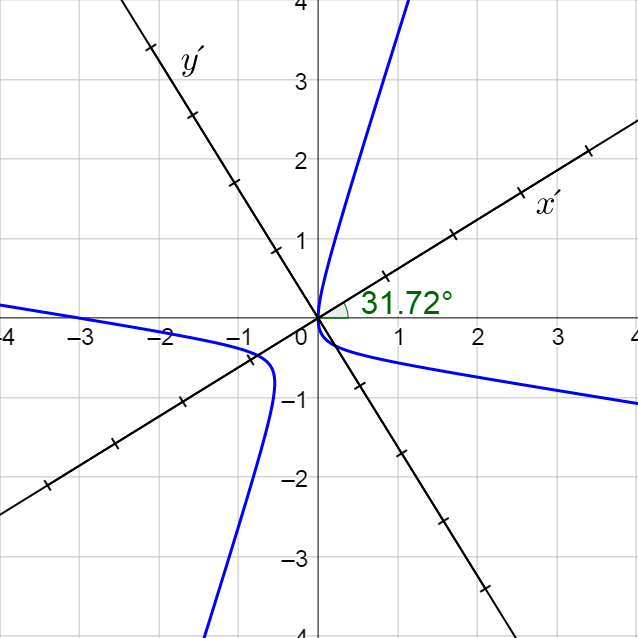
  2. Classify the graph using the discriminant. B2 – 4AC = (−2)2 – 4(2)(1)= −4 < 0, so it is an ellipse.

    To solve for y, rearrange the terms in powers of y and factor.

    $$2x^2 - 2xy + y^2 - 2y = 0$$

    $$y^2 + (-2xy - 2y) + 2x^2 = 0$$

    $$y^2 + (-2x - 2)y + 2x^2 = 0$$

    Now fill in the quadratic formula: \(y = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}\).

    $$y = \frac{-(-2x - 2) ± \sqrt{(-2x - 2)^2 - 4(1)(2x^2)}}{2(1)}$$

    Because of the ± sign, you will have to input two equations, one with + and one with −, to make the graph. Notice that the graph is shifted and (0, 0) is not the center.

    Figure 7: 2x2 – 2xy + y2 – 2y = 0.

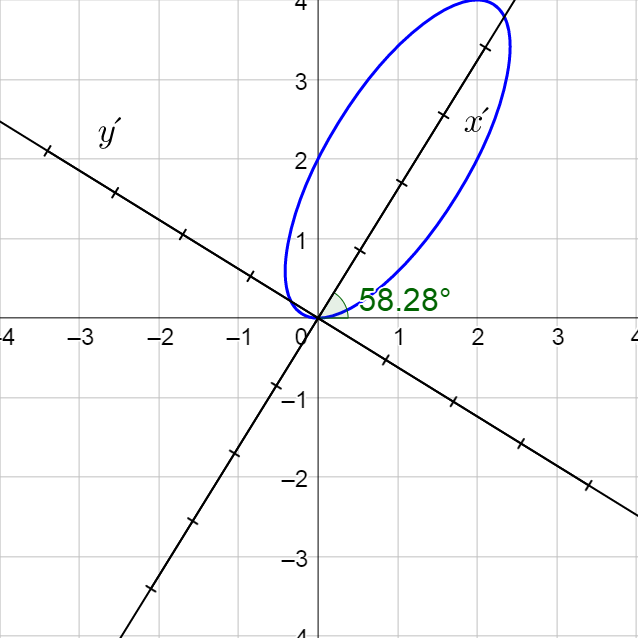
  3. Classify the graph using the discriminant. B2 – 4AC = (−4)2 – 4(4)(1) = 0, so it is a parabola.

    To solve for y, rearrange the terms in powers of y and factor.

    $$4x^2 - 4xy + y^2 - x + y = 0$$

    $$y^2 + (-4xy + y^2) + (4x^2 - x) = 0$$

    $$y^2 + (-4x + 1)y + (4x^2 - x) = 0$$

    Now fill in the quadratic formula: \(y = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}\).

    $$y = \frac{-(-4x + 1) ± \sqrt{(-4x + 1)^2 - 4(1)(4x^2 - x)}}{2(1)}$$

    Because of the ± sign, you will have to input two equations, one with + and one with −, to make the graph. Notice that the graph is shifted and (0, 0) is not the vertex.

    Figure 8: 4x2 − 4xy + y2 − x + y = 0.
Try It 5

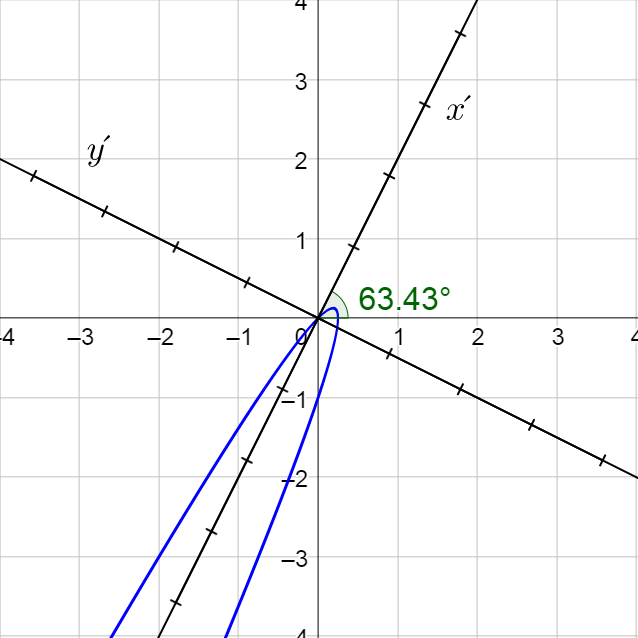
Classify the conic and graph it on a graphing utility.

  1. 2x2 + 3xy − y2 − 1 = 0
  2. x2 − 2xy + y2 − 2x = 0
Answers

(a) Hyperbola; 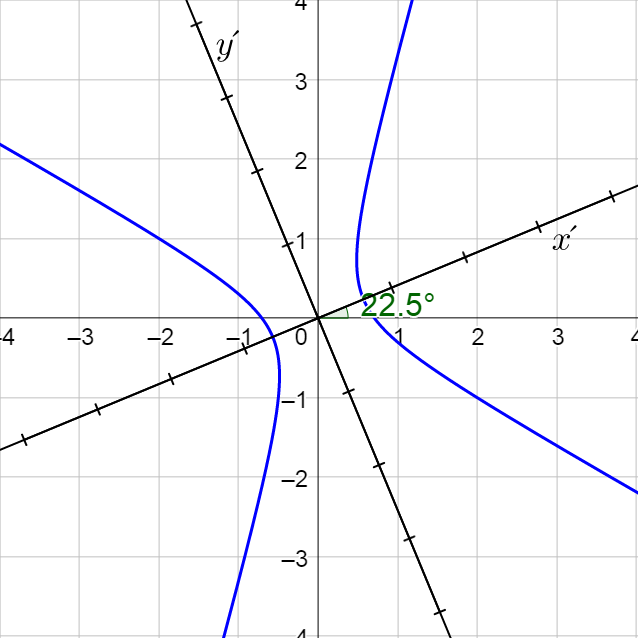(b) Parabola;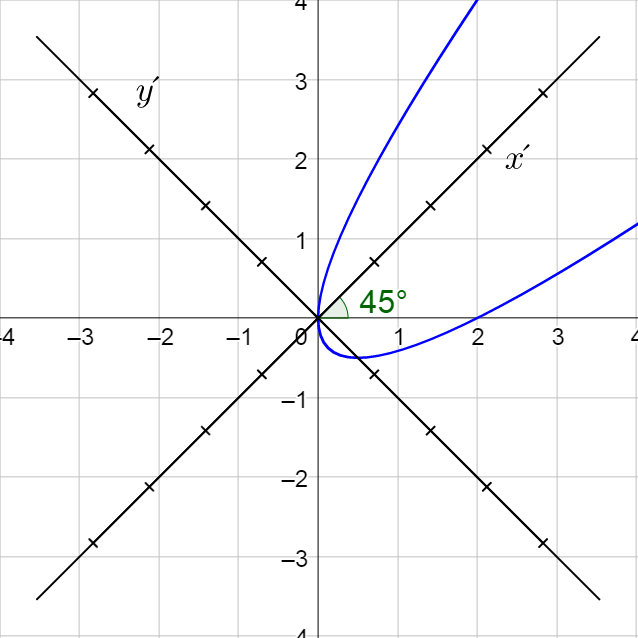

Lesson Summary
Classify Rotated Conics

If the conic is in the form Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 and B ≠ 0, then conic can be classified by

Writing Rotated Conics in Standard Form

Given a conic written as Ax2 + Bxy + Cy2 + Dx + Ey + F = 0 where B ≠ 0

  1. Find the angle of rotation using

    $$\cot 2θ = \frac{A - C}{B}$$

    where 0 < θ < \(\frac{π}{2}\).

  2. Find sin θ and cos θ.

    If θ is a special angle, evaluate sin θ and cos θ directly.

    If θ is not a special angle,

    1. Find cot 2θ.
    2. Reciprocal to find tan 2θ.
    3. Use 1 + tan2 u = sec2 u to find sec 2θ. (If tan 2θ < 0, then sec 2θ < 0.)
    4. Reciprocal to find cos 2θ.

    5. Use the half-angle formulas to find sin θ and cos θ.

      $$\sin θ = \sqrt{\frac{1 - \cos 2θ}{2}} \text{ and } \cos θ = \sqrt{\frac{1 + \cos 2θ}{2}}$$

  3. Find the substitutions for x and y using

    $$\begin{alignat}{2}x &= x′ \cos θ &&- y′ \sin θ\\y &= x′ \sin θ &&+ y′ \cos θ\end{alignat}$$

  4. Make the substitutions and arrange the terms into standard form.
Graph a Rotated Conic
  1. Draw the rotated axes.
  2. Using the rotated axes, sketch the conic.
Graph a Rotated Conic on a Graphing Calculator
  1. Arrange the terms in descending powers of y.
  2. Group the terms by the powers of y. Factor the y2 and factor the y.
  3. Fill in the quadratic formula, \(y = \frac{-b ± \sqrt{b^2 - 4ac}}{2a}\), where a is the expression multiplied with the y2, b is the expression multiplied with the y, and c is the expression without a y.
  4. Because of the ±, two equations will have to be entered into the calculator; one just + and the other just −.

Helpful videos about this lesson.

Practice Exercises

  1. When you are using \(\cot 2θ = \frac{A - C}{B}\) and get a negative angle, how do you get the correct positive angle? Do you do this before or after dividing by 2?

    2. Classify the conic and rewrite it in standard form by eliminating the Bxy term.

  2. 2xy = −9
  3. 7x2 + 4xy + 7y2 − 45 = 0
  4. \(x^2 - 2\sqrt{3} xy + 3 y^2 + 8\sqrt{3} x + 8 y = 0\)
  5. \(24x^2 - 2\sqrt{3}xy + 22y^2 - 525 = 0\)

    6. Classify the conic, rewrite it in standard form, and sketch its graph.

  6. 7x2 − 50xy + 7y2 + 72 = 0
  7. x2 + 4xy + 4y2 − 4x + 2y = 0
  8. 6x2 + 12xy + y2 + 3 = 0
  9. 14x2 + 15xy + 6y2 − \(\frac{27}{2}\) = 0
  10. 2x2 + 3xy − 2y2 − 10 = 0

    11. Classify the conic and sketch its graph using a graphing utility.

  11. x2 + 2xy + y2 + 2x = 0
  12. 2x2 + 5xy + y2 − 3x = 0
  13. x2 + 5xy + y2 − 4y = 0
  14. x2 − 2xy + 2y2 + 2x − 3y = 0
  15. 4x2 − 4xy + y2 − 5y − 7 = 0

    16. Mixed Review

  16. (7-04) Sketch a graph of \(\frac{y^2}{16} - \frac{x^2}{4} = 1\).
  17. (7-03) Sketch a graph of \(\frac{x^2}{4} + \frac{y^2}{16} = 1\).
  18. (7-02) Sketch a graph of x2 = −12y.
  19. (7-01) Sketch a graph of a line with inclination of \(\frac{π}{4}\) and goes through (0, 0).
  20. (6-03) Evaluate \(\langle 2, -3\rangle + 2\langle 0, 1\rangle\).

Answers

  1. Add π before dividing by 2
  2. Hyperbola; \(\frac{(y′)^2}{9} - \frac{(x′)^2}{9} = 1\)
  3. Ellipse; \(\frac{(x′)^2}{5} + \frac{(y′)^2}{9} = 1\)
  4. Parabola; (y′)2 = -4x′
  5. Ellipse; \(\frac{(x′)^2}{25} + \frac{(y′)^2}{21} = 1\)
  6. Hyperbola; \(\frac{(x′)^2}{4} - \frac{4(y′)^2}{9} = 1\);
  7. Parabola; \(\left(x′\right)^2 = -\frac{2\sqrt{5}}{5}y′\);
  8. Hyperbola; \(\left(y′\right)^2 - \frac{10\left(x′\right)^2}{3} = 1\);
  9. Ellipse; \(\frac{13\left(x′\right)^2}{9} + \frac{\left(y′\right)^2}{9} = 1\);
  10. Hyperbola; \(\frac{\left(x′\right)^2}{4} - \frac{\left(y′\right)^2}{4} = 1\);
  11. Parabola;
  12. Hyperbola;
  13. Hyperbola;
  14. Ellipse;
  15. Parabola;
  20. \(\langle2, -1\rangle\)