Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


And surely I am with you always, to the very end of the age. Matthew 28:20b NIV

7-04 Hyperbolas

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.6.7

cooling towers
Cooling towers. (pixabay/jplenio)

When designing cooling towers for power plants, engineers needed to find a shape that withstands high winds and is built with as little material as possible. A hyperbolic shape solves both problems. In addition, the shape helps the cooling air naturally rise.

Hyperbolas

Hyperbolas are the set of all points in a plane where the difference of the distances from two set points, foci, is constant. In figure 2, d1 – d2 is constant.

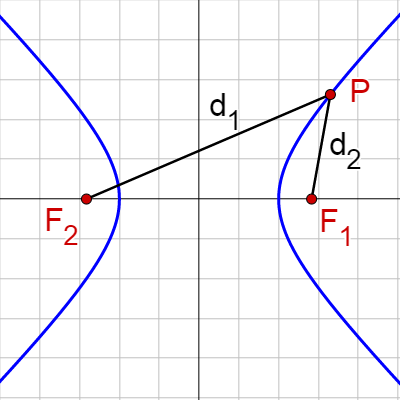
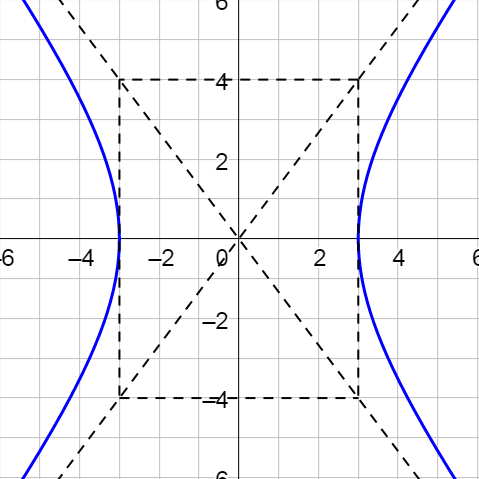
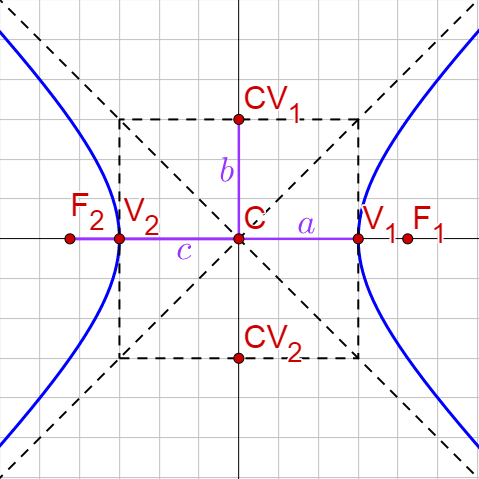
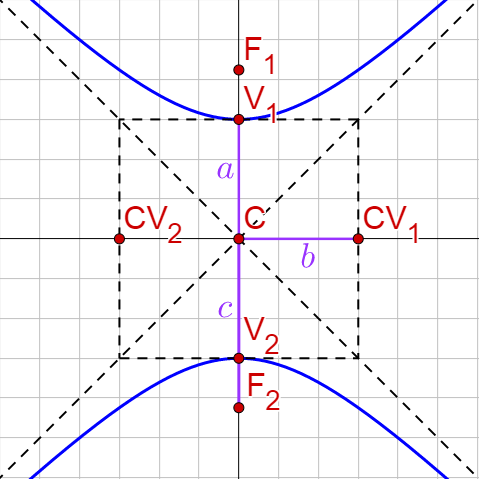
A hyperbola is the set of points where the difference of the distances, d1 – d2, is constant.

The vertices are the minimum/maximum of each branch of the hyperbola. The covertices are analogous to the covertices of the ellipse, but are not actually on the hyperbola. The transverse axis is the segment connecting the vertices, and the conjugate axis is the segment connecting the covertices. A box with the vertices and covertices as midpoints of the sides provides an aid for sketching the graph of the hyperbola. The branches are asymptotic with the asymptotes going through the corners of the box.

Horizontal Hyperbola
Vertical Hyperbola
Center: (h, k)
Horizontal transverse axis length = 2a
Vertical conjugate axis length = 2b
c2 = a2 + b2
Vertices: (h ± a, k)
Covertices: (h, k ± b)
Foci: (h ± c, k)
Asymptotes: \(y = k ± \frac{b}{a}(x - h)\)
Standard Equation: \(\frac{\left(x - h\right)^2}{a^2} - \frac{\left(y - k\right)^2}{b^2} = 1\)		 Center at (h, k)
Vertical transverse axis length = 2a
Horizontal conjugate axis length = 2b
c2 = a2 + b2
Vertices (h, k ± a)
Covertices (h ± b, k)
Foci (h, k ± c)
Asymptotes: \(y = k ± \frac{a}{b}(x - h)\)
Standard Equation: \(\frac{\left(y - k\right)^2}{a^2} - \frac{\left(x - h\right)^2}{b^2} = 1\)

Eccentricity is \(e = \frac{c}{a}\) where e > 1. The larger the eccentricity is, the closer the branches are to straight lines.

Find the Parts of a Hyperbola

Find the center, vertices, asymptotes, and foci of the hyperbola given by 16x2 − 4y2 = 64.

Solution

Write the equation in standard form by dividing by 64 so that the equation equals 1.

$$\frac{x^2}{4} - \frac{y^2}{16} = 1$$

Because x comes first, this is a horizontal hyperbola. Compare this equation with the standard form, \(\frac{\left(x - h\right)^2}{a^2} - \frac{\left(y - k\right)^2}{b^2} = 1\), to see that h = 0, k = 0, a2 = 9 so a = 3, and b2 = 4 so b = 2.

c2 = a2 + b2

c2 = 4 + 16 = 20

$$c = 2\sqrt{5}$$

Center is (0, 0).

Vertices are (±2, 0).

Covertices are (0, ±4).

Asymptotes are y = ±2x.

Foci are (\(±2\sqrt{5}\), 0).

Find the center, vertices, covertices, asymptotes, and foci of \(\frac{(y - 2)^2}{36} - \frac{(x + 5)^2}{49} = 1\).

Answer

C(−5, 2), V(−5, −4) and (−5, 8), CV(−12, 2) and (2, 2), Asymptotes: \(y = 2 ± \frac{6}{7}(x + 5)\), F(-5, 2 ± \(\sqrt{85}\))

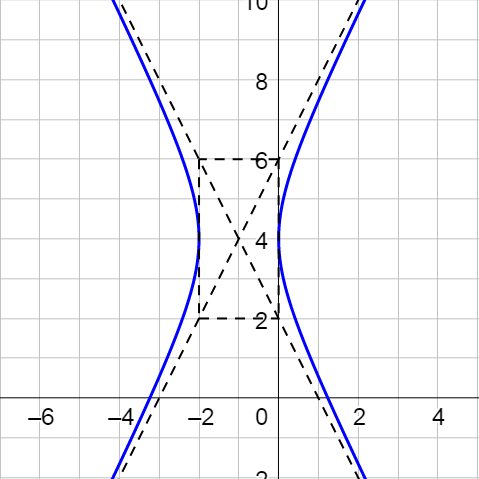
Find the Standard Equation of a Hyperbola

Find the standard form of the equation of the hyperbola centered at (−3, 1) with transverse axis length 6 and foci at (−3, −4) and (−3, 6). Then graph the hyperbola.

Solution

Graphing the three points shows that the transverse axis is vertical.

The transverse axis length is 2a = 6, so a = 3.

The distance from the center to the foci is c, so c = 5.

Find b

c2 = a2 + b2

52 = 32 + b2

b2 = 16

b = 4

The center is (−3, 1) so h = −3 and k = 1.

Write the standard form equation for a vertical hyperbola.

$$\frac{(y - 1)^2}{9} - \frac{(x + 3)^2}{16} = 1$$

Graph it by plotting the center.

Given that it is a vertical ellipse, move the distance a = 5 vertically from the center and a distance b = 4 horizontally from the center.

Draw a rectangle with these four points as the center of each side.

Draw diagonal lines through the corners of the rectangle. These are the asymptotes.

Sketch the hyperbola starting near an asymptote, curving through the vertex, and ending near the other asymptote.

\(\frac{(y - 1)^2}{9} - \frac{(x + 3)^2}{16} = 1\)

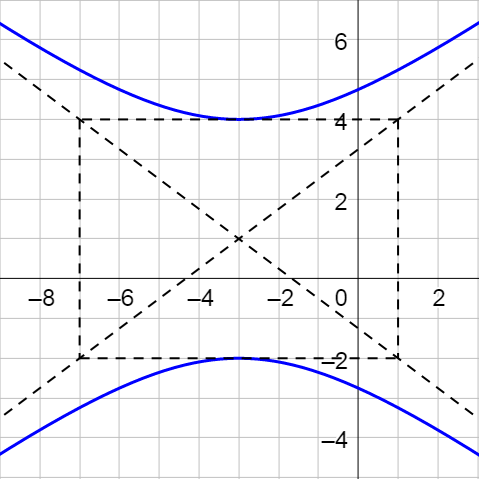
Find the standard form of the equation of the hyperbola with vertices at (1, 5) and (1, -3) and foci at (1, 7) and (1, -5). Then graph the hyperbola.

Answer

\(\frac{(y - 1)^2}{16} - \frac{(x - 1)^2}{20} = 1\),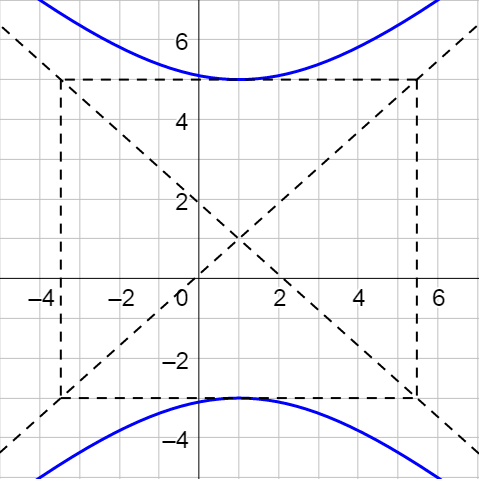

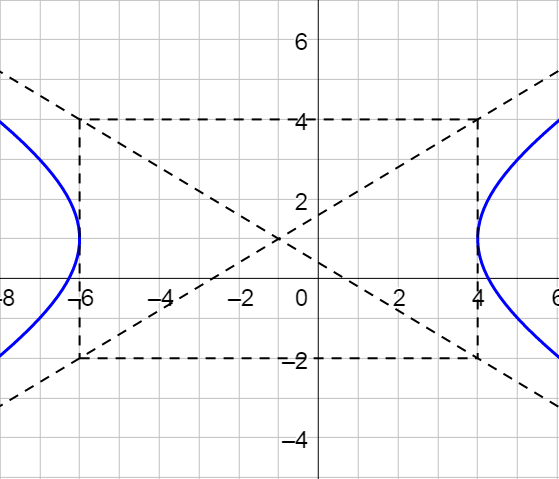
Graph a Hyperbola

Sketch the graph of the hyperbola given by 9x2 − 25y2 + 18x + 50y − 191 = 0.

Solution

Write the equation in standard form by completing the square. Start by moving the constant to the other side and factoring the x’s and y’s.

9(x2 + 2x) − 25(y2 − 2y) = 191

Add \(\left(\frac{1}{2} b\right)^2\) for both the x’s and y’s. On the right side, don’t forget to multiply by the coefficient.

$$9\left(x^2 + 2x + \left(\frac{1}{2} \left(2\right)\right)^2\right) - 25\left(y^2 - 2y + \left(\frac{1}{2}\left(-2\right)\right)^2\right) = 191 + 9\left(\frac{1}{2}\left(2\right)\right)^2 - 25\left(\frac{1}{2}\left(-2\right)\right)^2$$

9(x2 + 2x + 1) − 25(y2 − 2y + 1) = 191 + 9 − 25

Factor the left side.

9(x + 1)2 − 25(y − 1)2 = 175

Divide both sides by 175.

$$\frac{(x + 1)^2}{25} - \frac{(y - 1)^2}{9} = 1$$

This is a horizontal hyperbola.

The center is at (−1, 1), a = 5 and b = 3.

Go horizontally a = 5 from the center and vertically b = 3 from the center. These four points form the box. Draw the diagonals and then the hyperbola.

\(\frac{(x + 1)^2}{25} - \frac{(y - 1)^2}{9} = 1\)

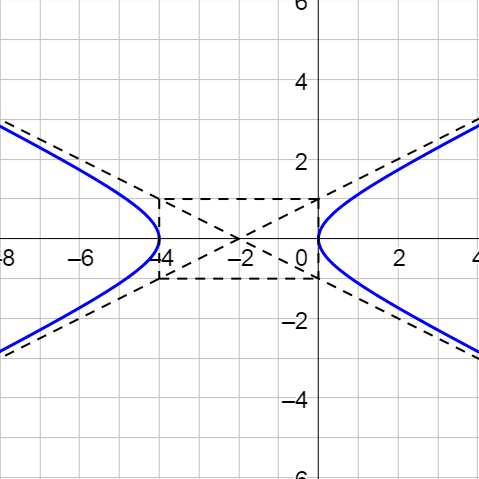
Sketch the graph of the hyperbola given by x2 − 4y2 + 4x = 0.

Answer

General Equations of Conics

All vertical and horizontal conics can be written in this general form.

Ax2 + Cy2 + Dx + Ey + F = 0

The conics can be classified by the following.

Classify Conics

If a conic is written in general form: Ax2 + Cy2 + Dx + Ey + F = 0

Classify Conics

Classify each conic.

  1. 16x2 − 3y2 + 9x − y + 16 = 0
  2. 7y2 + 2x − y + 4 = 0
  3. 4x2 + 3y2 − 7x + 2y − 1 = 0
  4. 3x2 + 3y2 + 2x + y + 4 = 0

Solution

Compare each equation to the general equation of a conic, Ax2 + Cy2 + Dx + Ey + F = 0, and find A and C. A is the coefficient of the x2 term and C is the coefficient of the y2 term.

  1. AC = 16(−3) = −48 < 0 so it is a hyperbola
  2. AC = 7(0) = 0 so it is a parabola
  3. AC = 4(3) = 12 > 0 so it is an ellipse
  4. A = C = 3 so it is a hyperbola

Classify each conic.

  1. 2x2 + 3y2 − x = 0
  2. 2x2 + 2x − y + 4 = 0

Answer

(a) Ellipse; (b) Parabola

Lesson Summary
Horizontal Hyperbola
Vertical Hyperbola
Center: (h, k)
Horizontal transverse axis length = 2a
Vertical conjugate axis length = 2b
c2 = a2 + b2
Vertices: (h ± a, k)
Covertices: (h, k ± b)
Foci: (h ± c, k)
Asymptotes: \(y = k ± \frac{b}{a}(x - h)\)
Standard Equation: \(\frac{\left(x - h\right)^2}{a^2} - \frac{\left(y - k\right)^2}{b^2} = 1\)		 Center at (h, k)
Vertical transverse axis length = 2a
Horizontal conjugate axis length = 2b
c2 = a2 + b2
Vertices (h, k ± a)
Covertices (h ± b, k)
Foci (h, k ± c)
Asymptotes: \(y = k ± \frac{a}{b}(x - h)\)
Standard Equation: \(\frac{\left(y - k\right)^2}{a^2} - \frac{\left(x - h\right)^2}{b^2} = 1\)
Classify Conics

If a conic is written in general form: Ax2 + Cy2 + Dx + Ey + F = 0

Helpful videos about this lesson.

Practice Exercises

  1. What is the difference between the transverse axis and the conjugate axis? How are they related to the major and minor axes of an ellipse?
  2. Find the center, vertices, asymptotes, and foci of the following hyperbolas.
  3. \(\frac{y^2}{64} - \frac{x^2}{16} = 1\)
  4. 20x2 − 25y2 − 200 = 0
  5. \(\frac{(x + 6)^2}{9} - \frac{(y - 3)^2}{8} = 1\)
  6. 100x2 − 81y2 + 200x + 648y + 6904 = 0
  7. Find the standard equation of the hyperbola with the following properties.
  8. Foci: (±4, 0), Vertices: (±2, 0)
  9. Vertices: (3, 4) and (3, 10), Covertices: (−1, 7) and (7, 7)
  10. Asymptotes: \(y = 3 ± \frac{2}{3} (x - 1)\), Vertex: (1, 7)
  11. Sketch the graph of the following hyperbolas.
  12. \(\frac{x^2}{9} - \frac{y^2}{16} = 1\)
  13. x2 − y2 − 6x + 4y + 9 = 0
  14. 4x2 − y2 + 8x + 8y − 16 = 0
  15. Eccentricity
  16. Find the standard equation of the hyperbola with \(e = \frac{4}{3}\) and vertices (±3, 0).
  17. What is the eccentricity of 16x2 − 9y2 + 96x + 36y − 36 = 0?
  18. Problem Solving
  19. (pixabay/Kurt Klement)
    The cooling tower at the electrical power generating station in Michigan City, Indiana, is modeled by a hyperbola and is about 300 feet tall. Write a model for the sides of the tower if the center is at (0, 200), the vertices are (±75, 200), and point at the base is (112.5, 0).
  20. Sundial in Cambridge, UK. (Richard Wright)
    A sundial is made of a rod that casts a shadow. The shadow falls on a scale to tell the time. The tip of the rod traces a hyperbola over the course of a day. This is called the declination line. If a certain declination line is modeled by \(\frac{y^2}{4} - \frac{x^2}{100} = 1\), what is its eccentricity?
  21. Mixed Review
  22. (7-03) Find the center, vertices, covertices, and foci of \(\frac{(x + 1)^2}{16} + \frac{(y - 4)^2}{9} = 1\).
  23. (7-03) Sketch the graph of x2 + 16y2 + 4x − 12 = 0.
  24. (7-02) Write the standard equation for the parabola with vertex (2, 3) and directrix y = −1.
  25. (7-01) Find the angle between y = −4x and 2x − y + 3 = 0.
  26. (2-04) Divide using synthetic division: (2x3 + 4x2 − x + 3) ÷ (x + 1).

Answers

  1. The vertices are on the transverse axis. The covertices are on the conjugate axis.
  2. C(0, 0), V(0, ±8), A: y = ±2x, F(0, ±\(4\sqrt{5}\))
  3. C(0, 0), V(\(±\sqrt{10}\), 0), A: \(y = ±\frac{2\sqrt{5}}{5} x\), F(±\(3\sqrt{2}\), 0)
  4. C(−6, 3), V(−9, 3) and (−3, 3), A: \(y = 3 ±\frac{2\sqrt{2}}{3} (x + 6)\), F(\(-6 ± \sqrt{17}\), 3)
  5. C(−1, 4), V(−1, −6) and (−1, 14), A: \(y = 4 ±\frac{10}{9} (x + 1)\), F(-1, 4 ± \(\sqrt{181}\))
  6. \(\frac{x^2}{4} - \frac{y^2}{12} = 1\)
  7. \(\frac{(y - 7)^2}{9} - \frac{(x - 3)^2}{16} = 1\)
  8. \(\frac{(y - 3)^2}{16} - \frac{(x - 1)^2}{36} = 1\)
  12. \(\frac{x^2}{9} - \frac{y^2}{7} = 1\)
  13. \(\frac{5}{3}\)
  14. \(\frac{x^2}{5625} - \frac{(y - 200)^2}{32000} = 1\)
  15. 5.099
  16. C(−1, 4), V(−5, 4) and (3, 4), CV(−1, 1) and (−1, 7), F(−1 ± \(\sqrt{7}\), 4)
  18. (x − 2)2 = 16(y − 3)
  19. 40.60°
  20. \(2x^2 + 2x - 3 + \frac{6}{x + 1}\)