Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Trust in the Lord with all your heart and lean not on your own understanding; in all your ways submit to him, and he will make your paths straight. Proverbs 3:5-6 NIV

7-03 Ellipses and Circles

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.6.7

Planets.
The planets orbiting the sun. (NASA/JPL)

Planets orbit the sun in an elliptical orbit with the sun at one focus. This is true for all bodies orbiting by gravity such as moons, comets, and satellites. The orbits of planets are almost circular, but comets' orbits are very elliptical.

Ellipses

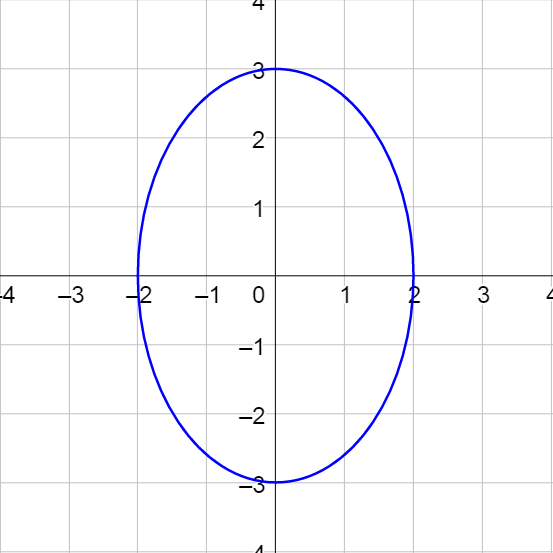
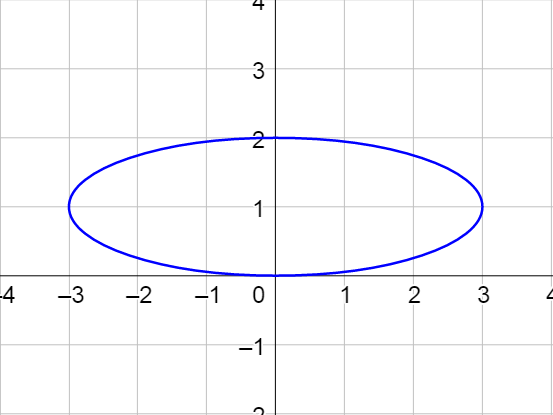
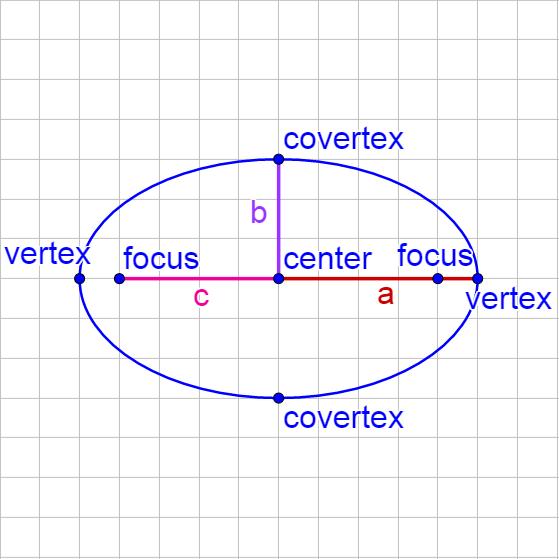
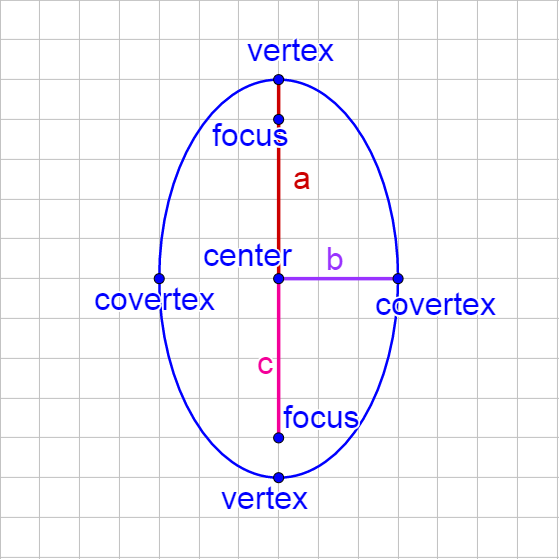
An ellipse is the set of all points in a plane where the sum of the distances to two fixed points, called foci, is constant. A circle is a special form of an ellipse where both foci are at the center. The major axis is the longest segment across the ellipse and connects the two vertices. The minor axis is the shortest segment across the ellipse and connects the two covertices.

Horizontal Ellipse
Vertical Ellipse
Center: (h, k)
Horizontal major axis length = 2a
Vertical minor axis length = 2b
c2 = a2 − b2
Vertices: (h ± a, k)
Covertices: (h, k ± b)
Foci: (h ± c, k)
Standard Equation: \(\frac{\left(x - h\right)^2}{a^2} + \frac{\left(y - k\right)^2}{b^2} = 1\)		 Center at (h, k)
Vertical major axis length = 2a
Horizontal minor axis length = 2b
c2 = a2 – b2
Vertices (h, k ± a)
Covertices (h ± b, k)
Foci (h, k ± c)
Standard Equation: \(\frac{\left(x - h\right)^2}{b^2} + \frac{\left(y - k\right)^2}{a^2} = 1\)

In both cases,

Find the Parts of an Ellipse

Find the center, vertices, and foci of the ellipse given by 4x2 + 25y2 = 100.

Solution

Put the equation in standard form by dividing by 100 so the equation equals 1.

$$\frac{x^2}{25} + \frac{y^2}{4} = 1$$

The bigger denominator is a2. Since x is above the a2, the ellipse is horizontal.

Compare this to the standard horizontal equation, \(\frac{\left(x - h\right)^2}{a^2} + \frac{\left(y - k\right)^2}{b^2} = 1\), to find:

a2 = 25 so a = 5

b2 = 4 so b = 2

c2 = a2 – b2 so c2 = 52 – 22. \(c = \sqrt{21}\).

Also, h = 0, k = 0, so the center is (0, 0).

Vertices are (h ± a, k) = (±5, 0).

Covertices are (h, k ± b) = (0, ±2).

Foci are (h, k ± c) = \(\left(±\sqrt{21}, 0\right)\)

Find the center, vertices, covertices, and foci of the ellipse given by 81x2 + 16y2 = 1296.

Answer

Center: (0, 0); Vertices: (0, ±9); Covertices: (±4, 0); Foci: \((0, ±\sqrt{65})\)

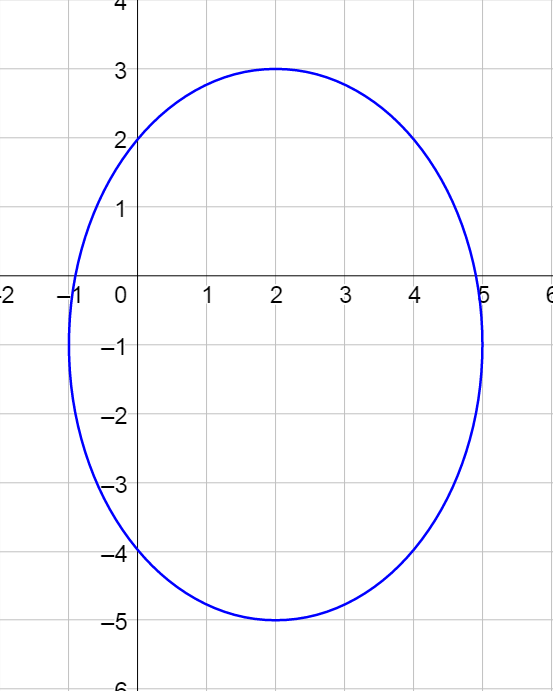
Write the Standard Equation of an Ellipse

Find the standard form of the equation of the ellipse centered at (−2, 3) with major axis length 10 and foci at (−2, 0) and (−2, 6). Then graph the ellipse.

Solution

Graph the center and the foci. Notice that the major axis through the points is vertical, so this is a vertical ellipse.

The center and foci.

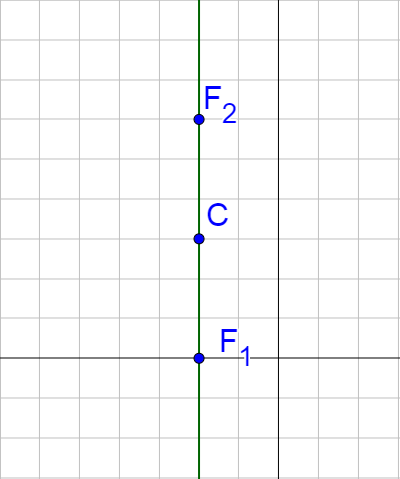
The center is (−2, 3) = (h, k).

The major axis length is 10 = 2a, so a = 5.

c is the distance from the center to the foci, so c = 3.

c2 = a2 − b2, so 32 = 52 – b2.

b2 = 52 – 32 = 16, so b = 4.

Now write the equation by filling in the standard equation.

$$\frac{\left(x - h\right)^2}{b^2} + \frac{\left(y - k\right)^2}{a^2} = 1$$

$$\frac{\left(x + 2\right)^2}{25} + \frac{\left(y - 3\right)^2}{16} = 1$$

The vertices are (h, k ± a) = (−2, 2) and (−2, 8).

The covertices are (h ± b, k) = (−6, 3) and (2, 3).

Graph by plotting the vertices and covertices, then drawing an approximate ellipse.

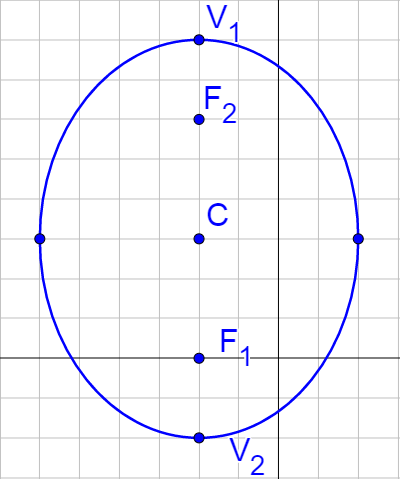
\(\frac{\left(x + 2\right)^2}{25} + \frac{\left(y - 3\right)^2}{16} = 1\)

Find the standard equation of the ellipse with vertices (−1, 4) and (5, 4) and covertices (2, 3) and (2, 5).

Answer

\(\frac{\left(x - 2\right)^2}{9} + \left(y - 4\right)^2 = 1\)

Graph an Ellipse

Sketch the graph of the following ellipse:

4x2 + 9y2 − 8x + 54y + 49 = 0

Solution

Complete the square by moving the constant to the other side and factoring the x’s and y’s.

4(x2 − 2x) + 9(y2 + 6y) = −49

Add \(\left(\frac{1}{2} b\right)^2\) for both the x’s and y’s. On the right side, don’t forget to multiply by the coefficient.

$$4\left(x^2 - 2x + \left(\frac{1}{2} (-2)\right)^2\right) + 9\left(y^2 + 6y + \left(\frac{1}{2} (4)\right)^2\right) = -49 + 4\left(\left(\frac{1}{2} (-8)\right)^2\right) + 9\left(\left(\frac{1}{2} (4)\right)^2\right)$$

4(x2 − 2x + 1) + 9(y2 + 6y + 9) = −211 + 4 + 81

Factor the left side.

4(x − 1)2 + 9(y + 3)2 = 36

Divide by 36 to make the equation equal 1.

$$\frac{\left(x - 1\right)^2}{9} + \frac{\left(y + 3\right)^2}{4} = 1$$

The larger number is under x, so this must be a horizontal ellipse. Compare the equation to the standard form, \(\frac{\left(x - h\right)^2}{a^2} + \frac{\left(y - k\right)^2}{b^2} = 1\), and see that h = 1, k = −3, a2 = 9 so a = 3, and b2 = 4 so b = 2.

Graph by plotting the center. From the center move in the x-direction a = 3 since it is under the x to plot the vertices. Move b = 2 in the y-direction since it is under the y to plot the covertices. Sketch an ellipse through these points.

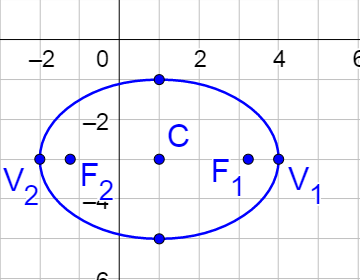
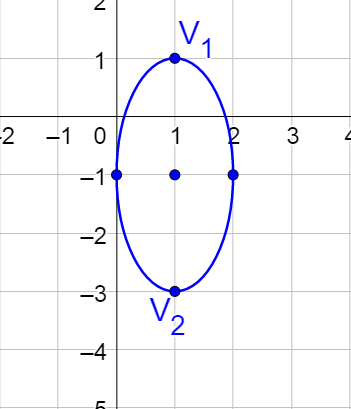
\(\frac{\left(x - 1\right)^2}{9} + \frac{\left(y + 3\right)^2}{4} = 1\)

Sketch the graph of the ellipse given by 4x2 + y2 − 8x + 2y + 1 = 0.

Answer

Eccentricity

Eccentricity is a measure of how circular an ellipse is. \(e = \frac{c}{a}\) where 0 < e < 1. If the eccentricity is near 0, then the ellipse is almost a circle. If the eccentricity is near 1, then the ellipse is almost a line.

Model an Orbit

Halley's Comet. (NASA/W. Liller)

Halley's Comet orbits the sun with an eccentricity of 0.967. If the major axis is 35.8 AU, find an equation to model the orbit. Use a horizontal ellipse with the center at the origin.

Solution

a is half of the major axis, so \(a = \frac{1}{2} 35.8 = 17.6 \text{ AU}\). Now use the eccentricity to find c.

$$e = \frac{c}{a}$$

$$0.967 = \frac{c}{17.6}$$

c ≈ 17.0192

Because the orbit is an ellipse, c2 = a2 − b2.

(17.0192)2 = (17.6)2 − b2

b2 = 20.1068

Now fill in the standard form of a horizontal ellipse, \(\frac{\left(x - h\right)^2}{a^2} + \frac{\left(y - k\right)^2}{b^2} = 1\), with the center at (0, 0).

$$\frac{\left(x - 0\right)^2}{\left(17.6\right)^2} + \frac{\left(y - 0\right)^2}{20.1068} = 1$$

$$\frac{x^2}{309.76} + \frac{y^2}{20.11} = 1$$

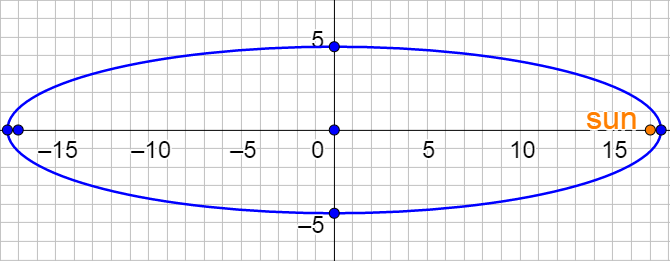
Orbit of Halley's Comet around the sun

Find the equation of a vertical ellipse with the center at (2, 4), major axis of 8, and eccentricity of 0.5.

Answer

\(\frac{\left(x - 2\right)^2}{16} + \frac{\left(y - 4\right)^2}{12} = 1\)

Lesson Summary
Horizontal Ellipse
Vertical Ellipse
Center: (h, k)
Horizontal major axis length = 2a
Vertical minor axis length = 2b
c2 = a2 − b2
Vertices: (h ± a, k)
Covertices: (h, k ± b)
Foci: (h ± c, k)
Standard Equation: \(\frac{\left(x - h\right)^2}{a^2} + \frac{\left(y - k\right)^2}{b^2} = 1\)		 Center at (h, k)
Vertical major axis length = 2a
Horizontal minor axis length = 2b
c2 = a2 – b2
Vertices (h, k ± a)
Covertices (h ± b, k)
Foci (h, k ± c)
Standard Equation: \(\frac{\left(x - h\right)^2}{b^2} + \frac{\left(y - k\right)^2}{a^2} = 1\)

Helpful videos about this lesson.

Practice Exercises

  1. What is the difference between vertices and covertices?
  2. Find the center, vertices, covertices, and foci of the following ellipses.
  3. \(\frac{x^2}{625} + \frac{y^2}{49} = 1\)
  4. 36x2 + 16y2 − 576 = 0
  5. \(\frac{\left(x - 3\right)^2}{9} + \frac{\left(y + 2\right)^2}{36} = 1\)
  6. 12x2 + 5y2 + 48x + 10y − 7 = 0
  7. Find the standard equation of the ellipse with the following properties.
  8. Vertices: (0, ±5), Foci: (0, ±1)
  9. Vertices: (5, 1) and (−7, 1), Covertices: (−1, 4) and (−1, −2)
  10. Foci: (2, 4) and (2, 0), Covertices: (5, 2) and (−1, 2)
  11. Sketch the graph of the following ellipses.
  12. \(\frac{x^2}{4} + \frac{y^2}{9} = 1\)
  13. x2 + 9y2 − 18y = 0
  14. 16x2 + 9y2 − 64x + 18y − 71 = 0
  15. Eccentricity
  16. Find the eccentricity of the ellipse \(\frac{\left(x + 5\right)^2}{169} + \frac{y^2}{144} = 1\).
  17. Find the standard equation of the ellipse with eccentricity of \(\frac{2}{3}\) and vertices (−2, 8) and (−2, −4).
  18. Problem Solving
  19. (wikimedia/NASA/JPL/USGS)
    Mars orbits the sun in an elliptical orbit with a semimajor (half the major) axis of 1.524 astronomical units and eccentricity of 0.0934. Find the equation of the orbit with the sun at a focus, the center at (0, 0), and a vertical standard equation.
  20. (wikimedia/NASA/JPL)
    An equation that models the moon’s orbit around the earth is \(\frac{x^2}{1.4803×10^{11}} + \frac{y^2}{1.4758×10^{11}} = 1\). Find the eccentricity of the moon’s orbit.
  21. Mixed Review
  22. (7-02) Find the vertex, focus, and directrix of y2 − 6x − 6y − 3 = 0.
  23. (7-02) Write the standard equation for the parabola with vertex (3, 0) and directrix x = 0.
  24. (7-01) Find the distance from the point (5, 1) to the line 2x − y + 1 = 0.
  25. (6-05) Evaluate ⟨2, 0⟩ · ⟨0, −4⟩.
  26. (6-03) Evaluate ⟨2, 0⟩ + ⟨0, −4⟩ both graphically and algebraically.

Answers

  1. Vertices are the ends of the major axis, and covertices are the ends of the minor axis.
  2. C(0, 0); V(±25, 0); CV(0, ±7); F(±24, 0)
  3. C(0, 0); V(0, ±6); CV(±4, 0); F(0, ±\(2\sqrt{5}\))
  4. C(3, −2); V(3, −8), (3, 4); CV(0, −2), (6, −2); F\(\left(3, -2 ± 3\sqrt{3}\right)\)
  5. C(−2, −1); V\(\left(-2, -1 ± 2\sqrt{3}\right)\); CV\(\left(-2 ± \sqrt{5}, -1\right)\); F\(\left(-2, -1 ± \sqrt{7}\right)\)
  6. \(\frac{x^2}{24} + \frac{y^2}{25} = 1\)
  7. \(\frac{\left(x + 1\right)^2}{36} + \frac{\left(y - 1\right)^2}{9} = 1\)
  8. \(\frac{\left(x - 2\right)^2}{9} + \frac{\left(y - 2\right)^2}{13} = 1\)
  12. \(e = \frac{5}{13}\)
  13. \(\frac{\left(x + 2\right)^2}{20} + \frac{\left(y - 2\right)^2}{36} = 1\)
  14. \(\frac{x^2}{2.302} + \frac{y^2}{2.323} = 1\)
  15. 0.055
  16. V(−2, 3), F(\(-\frac{1}{2}\), 3), D: \(x = -\frac{7}{2}\)
  17. y2 = 12(x − 3)
  18. \(2\sqrt{5}\)
  19. 0
  20. ⟨2, −4⟩