Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


But seek first his kingdom and his righteousness, and all these things will be given to you as well. Matthew 6:33 NIV

7-02 Parabolas

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.6.7

L'Umbracle sculpture garden in Valencia, Spain
L'Umbracle sculpture garden in Valencia, Spain. (pxhere.com)

The L'Umbracle sculpture garden is covered with arches shaped like parabolas that open down. Of all arch types, parabolic arches have the most thrust at their bases and can span the greatest distances when the weight is spread uniformly over the arch. Parabolas and similar curves are often used to make pleasing arches and shapes in buildings and bridges.

Parabolas

Parabolas are the set of all points in a plane that are equidistant from a fixed line, called the directrix and a fixed point, called the focus. The vertex is the maximum or minimum point and is the midpoint between the focus and directrix. The axis of symmetry is the line perpendicular to the directrix and goes through the focus and vertex. The parabola will bend around the focus and away from the directrix.

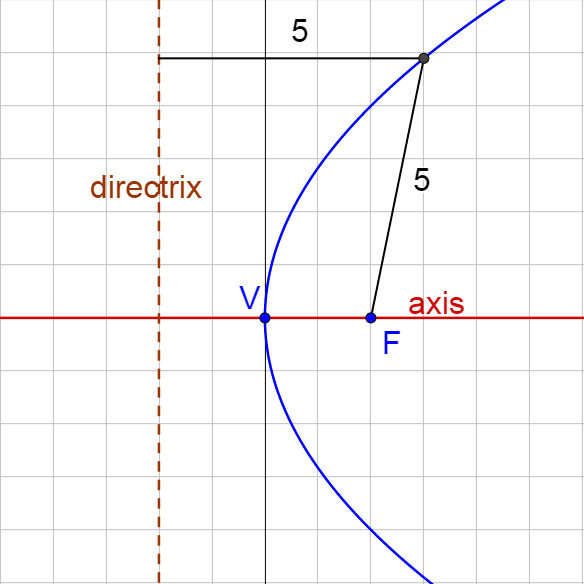
The distance to the focus equals the distance to the directrix from any point on the parabola.

Parabolas can be vertical so that they open up or down, or they can be horizontal opening left or right. The table gives information about the parts of a parabola.

Vertical Parabola
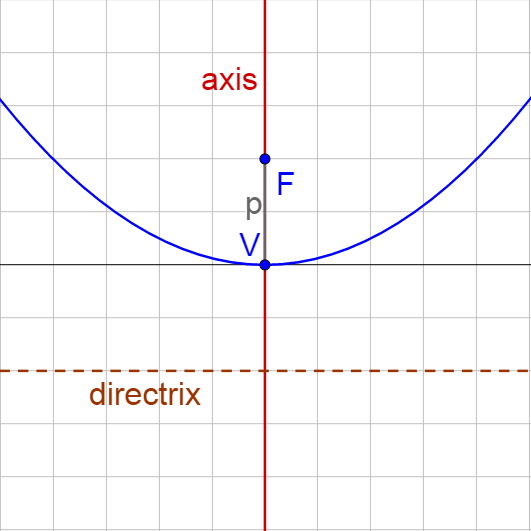
Horizontal Parabola
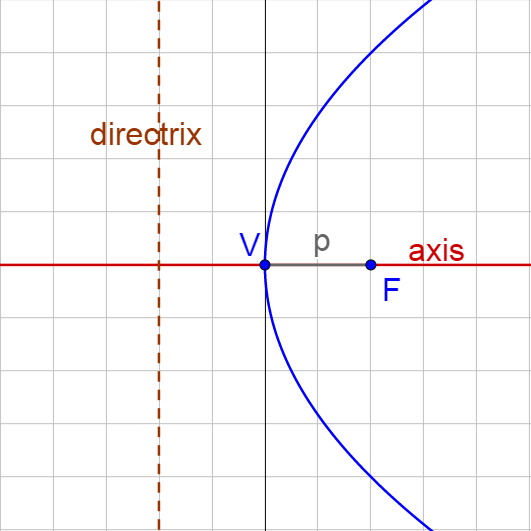p = the directed (+, −) distance from the vertex to the focus.
Vertex: (h, k)
Focus: (h, p + k)
Directrix: y = k – p
Standard Equation: (x − h)2 = 4p(y − k)		 p = the directed (+, −) distance from the vertex to the focus.
Vertex: (h, k)
Focus: (p + h, k)
Directrix: x = h – p
Standard Equation: (y − k)2 = 4p(x − h)

Graph a parabola by solving the equation for y, and making a table of values.

Find Parts of a Parabola

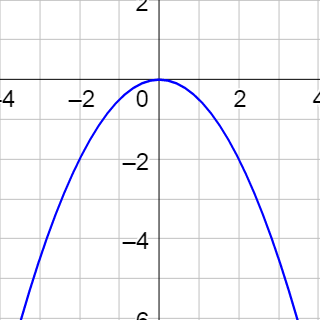
Find the vertex, focus, and directrix of the parabola given by \(y = \frac{1}{6}x^2\).

Solution

Rearrange the equation to fit the standard form.

x2 = 2y

Since it is x2, it is a vertical parabola. Compare it to the standard form equation.

(x − h)2 = 4p(y − k)

Notice that h = 0, k = 0, and 4p = 6 so \(p = \frac{3}{2}\).

The vertex is (h, k) = (0, 0).

The focus is (h, p + k) = \(\left(0, \frac{3}{2} + 0\right) = \left(0, \frac{3}{2}\right)\).

The directrix is y = k − p, so \(y = 0 - \frac{3}{2} \rightarrow y = -\frac{3}{2}\).

Find the vertex, focus, and directrix of the parabola given by x = 4y2.

Answer

Vertex: (0, 0); Focus: \(\left(\frac{1}{16}, 0\right)\); Directrix: \(x = -\frac{1}{16}\)

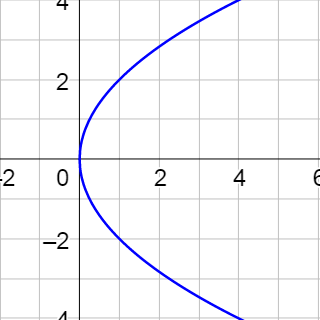
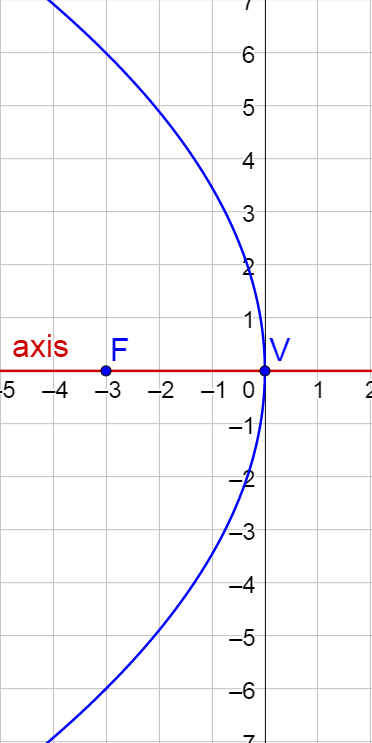
Write the Standard Equation of a Parabola

Find the standard form of the equation of a parabola with vertex at (0, 0) and focus (−3, 0). Then graph the parabola.

Solution

Graph the vertex and focus, and notice that the line through the two points is horizontal. This line is the axis.

The vertex and focus.

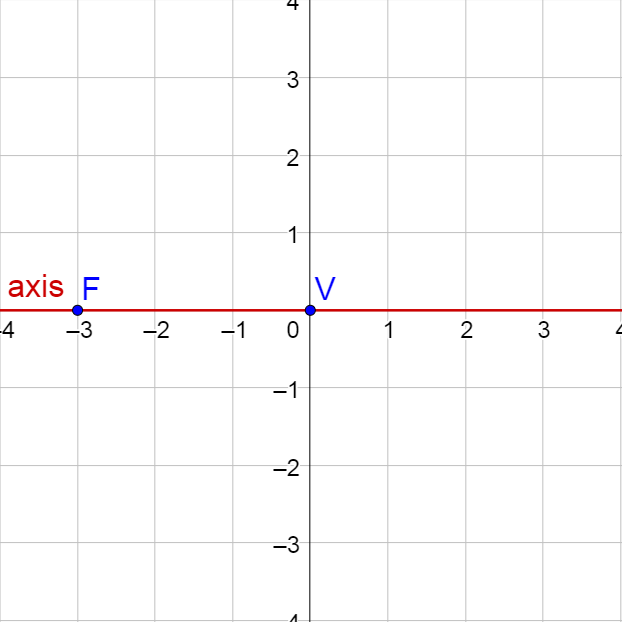
Since the vertex = (0, 0) = (h, k), both h = k = 0.

The distance from the vertex to the focus is 2 to the left, so p = −2.

Now fill out the standard form equation for a horizontal parabola.

(y − k)2 = 4p(x − h)

(y − 0)2 = 4(−3)(x − 0)

y2 = −12x

Graph the parabola by solving the equation for y.

$$y = ±\sqrt{-12x}$$

Now make a table of values. x-values greater than 0 produce imaginary results.

x y
−4 ±6.92
−3 ±6
−2 ±4.90
−1 ±3.46
0 0
\(y^2 = -12x\)

Find the standard form of the equation of a parabola with vertex at (0, 0) and focus (0, 4). Then graph the parabola.

Answer

x2 = 16y;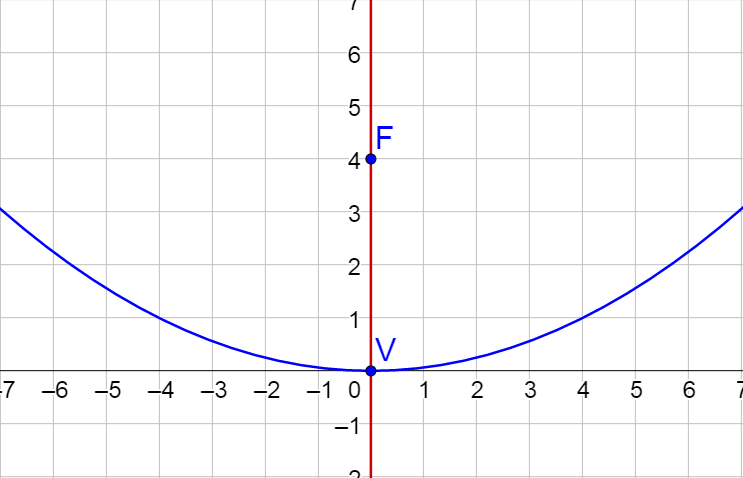

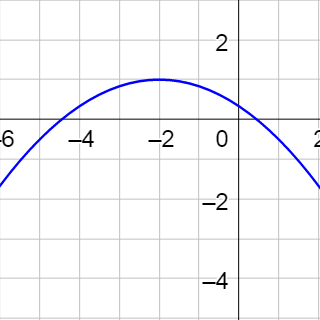
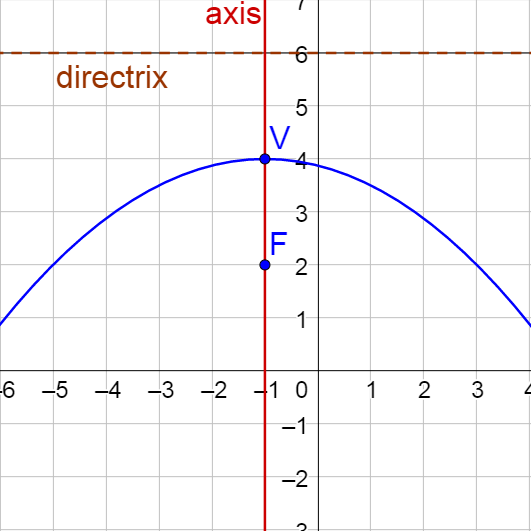
Find Parts of a Parabola

Find the vertex, focus, and directrix of the parabola given by x2 + 2x + 8y – 31 = 0. Then graph the parabola.

Solution

It is x2, so this is a vertical parabola.

Start arranging the terms to fit the standard form.

x2 + 2x = −8y + 31

Complete the square in the x by adding \(\left(\frac{1}{2} b\right)^2\) to each side of the equation.

$$x^2 + 2x + \left(\frac{1}{2}\left(2\right)\right)^2 = -8y + 31 + \left(\frac{1}{2}\left(2\right)\right)^2$$

x2 + 2x + 1 = −8y + 32

Factor both sides.

(x + 1)2 = −8(y − 4)

Now compare to the standard form equation.

(x − h)2 = 4p(y − k)

Notice that h = −1, k = 4, and 4p = −8 so p = −2.

The vertex is (−1, 4).

The focus is (−1, 2).

The directrix is y = 6.

Graph by solving for y and making a table of values.

(x + 1)2 = −8(y − 4)

$$\frac{\left(x + 1\right)^2}{-8} = y - 4$$

$$y = \frac{\left(x + 1\right)^2}{-8} + 4$$

x y
−4 2.88
−3 3.5
−2 3.88
−1 4
0 3.88
1 3.5
2 2.88
3 2
4 0.88
(x − 1)2 = 16(y + 2)

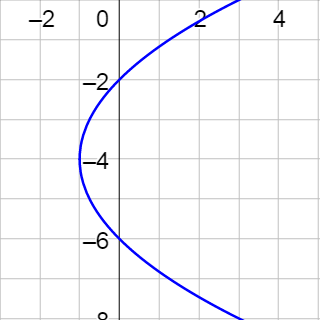
Find the vertex, focus, and directrix of the parabola given by y2 − 4x − 4y − 8 = 0. Then graph the parabola.

Answer

Vertex: (−3, 2); Focus: (−2, 2); Directrix: x = −4;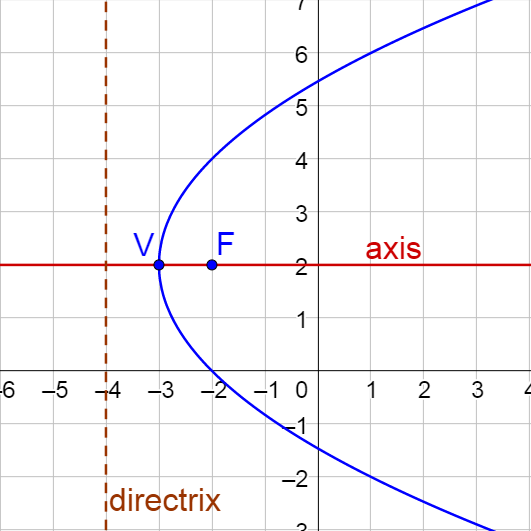

Write the Standard Equation of a Parabola

Write the standard form of the equation of the parabola with focus at (4, 1) and directrix x = −2.

Solution

The directrix is vertical, so the axis of the parabola is horizontal.

The focus is (4, 1) = (p + h, k), so k = 1.

Graph the directrix and the focus. The vertex is halfway in between the focus and directrix, (1, 1).

The directrix, focus, and vertex.

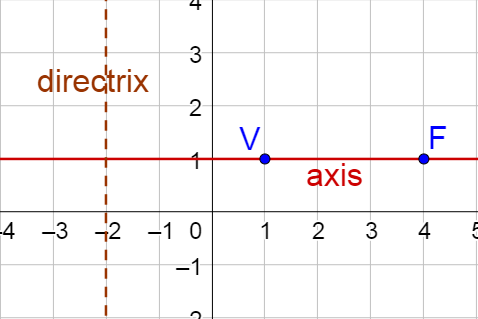
The distance from the vertex to the focus is 3 to the left, so p = −3.

Fill in the standard form equation for a horizontal parabola.

(y − k)2 = 4p(x − h)

(y − 1)2 = 4(−3)(x − 1)

(y − 1)2 = −12(x − 1)

Write the standard form of the equation of the parabola with focus at (0, −1) and directrix y = 3.

Answer

x2 = −8(y − 1)

Lesson Summary
Vertical Parabola
Horizontal Parabola
p = the directed (+, −) distance from the vertex to the focus.
Vertex: (h, k)
Focus: (h, p + k)
Directrix: y = k – p
Standard Equation: (x − h)2 = 4p(y − k)		 p = the directed (+, −) distance from the vertex to the focus.
Vertex: (h, k)
Focus: (p + h, k)
Directrix: x = h – p
Standard Equation: (y − k)2 = 4p(x − h)

Helpful videos about this lesson.

Practice Exercises

  1. Given the focus and directrix, (a) how do you find the vertex? and (b) how do you know which way the parabola opens?
  2. Find the vertex, focus, and directrix of the following equations.
  3. x2 = −8y
  4. 3y2 + 16x = 0
  5. (x − 1)2 = −16y
  6. y2 − 12x − 6y − 15 = 0
  7. Graph the parabolas.
  8. x2 = −2y
  9. y2 − 4x = 0
  10. (x + 2)2 = −6(y − 1)
  11. y2 − 4x + 8y + 12 = 0
  12. Write the standard equation for the parabola with the following properties.
  13. Focus: (5, 0), Directrix: x = −5
  14. Vertex: (0, 0), Directrix: y = 6
  15. Focus: (1, 4), Vertex: (1, 7)
  16. Focus: (−2, 5), Directrix: x = 1
  17. Problem Solving
  18. A thrown ball's path can be modeled by \(y = -\frac{1}{40} x^2 + x\) where x is the horizontal distance in feet and y is the vertical distance in feet from the point where the ball was thrown. What is the highest point of the ball's path?
  19. tyne bridge
    Tyne Bridge. (pixabay/Michaela Wenzler)
    The Tyne Bridge in northeast England links Newcastle upon Tyne with Gateshead. It consists of two parabolic arches with a roadway between. If the arch can be modeled by \(y = -\frac{1}{125} x^2 + \frac{27}{20} x\) where x is the horizontal distance in meters and y is the vertical distance in meters, find the height of the arch.
  20. Mixed Review
  21. (7-01) Find the inclination of the line that goes through (2, 1) and (5, −3).
  22. (7-01) Find the distance from P(0, 5) to the line y = 2x − 4.
  23. (6-05) Evaluate ⟨2, −4⟩ · ⟨−5, 3⟩.
  24. (4-02) Evaluate the six trigonometric functions for \(θ = \frac{5π}{6}\).
  25. (4-02) Evaluate the six trigonometric functions for \(θ = \frac{7π}{4}\).

Answers

  1. The vertex in the midpoint between the focus and the directrix; The parabola opens around the focus and away from the directrix.
  2. V(0, 0); F(0, -2); D: y = 2
  3. V(0, 0); F\(\left(-\frac{4}{3}, 0\right)\); D: \(x = \frac{4}{3}\)
  4. V(1, 0); F(1, −4); D: y = 4
  5. V(−2, 3); F(1, 3); D: x = −5
  10. y2 = 20x
  11. x2 = −24y
  12. (x − 1)2 = −12(y − 7)
  13. \(\left(y - 5\right)^2 = -6\left(x + \frac{1}{2}\right)\)
  14. (20, 10), so the ball is 10 feet high when it is 20 feet away from where it was thrown.
  15. 57.0 m
  16. 126.9°
  17. 4.02
  18. −22
  19. \(\sin \frac{5π}{6} = \frac{1}{2}\); \(\cos \frac{5π}{6} = -\frac{\sqrt{3}}{2}\); \(\tan \frac{5π}{6} = -\frac{\sqrt{3}}{3}\); \(\csc \frac{5π}{6} = 2\); \(\sec \frac{5π}{6} = -\frac{2\sqrt{3}}{3}\); \(\cot \frac{5π}{6} = -\sqrt{3}\)
  20. \(\sin \frac{7π}{4} = -\frac{\sqrt{2}}{2}\); \(\cos \frac{7π}{4} = \frac{\sqrt{2}}{2}\); \(\tan \frac{7π}{4} = -1\); \(\csc \frac{7π}{4} = -\sqrt{2}\); \(\sec \frac{7π}{4} = \sqrt{2}\); \(\cot \frac{7π}{4} = -1\)