Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
For I will forgive their wickedness and will remember their sins no more. Hebrews 8:12 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.7
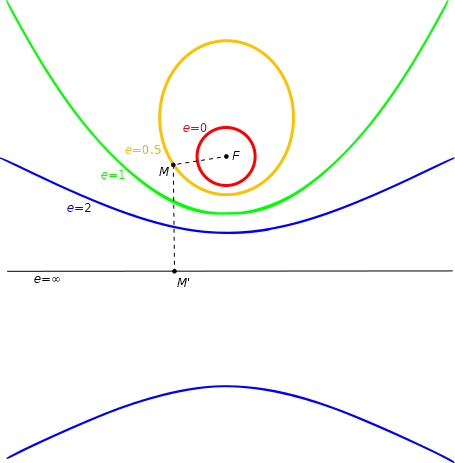
These graphs can all be generated from the same general equation. They are called conic sections and can be used in applications ranging as widely as the orbit of planets to the shape of the curve in a satellite dish.
Conic sections are the intersections of a plane with a double cone.
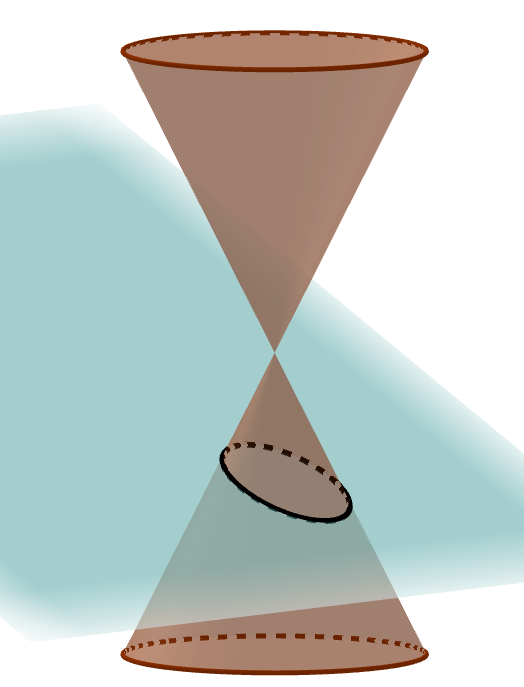
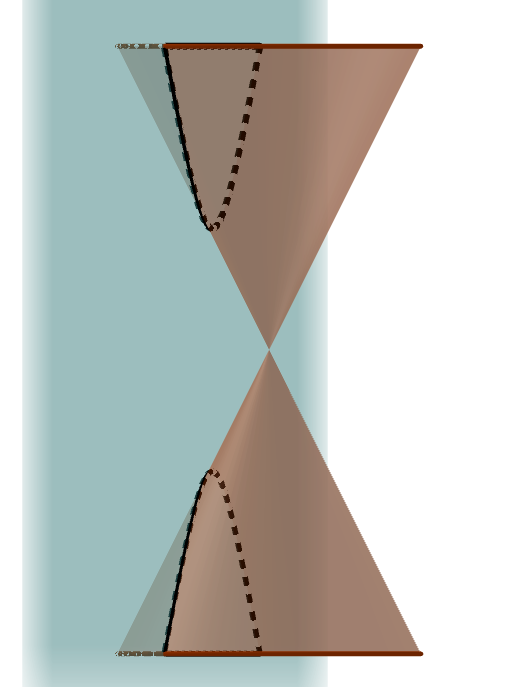
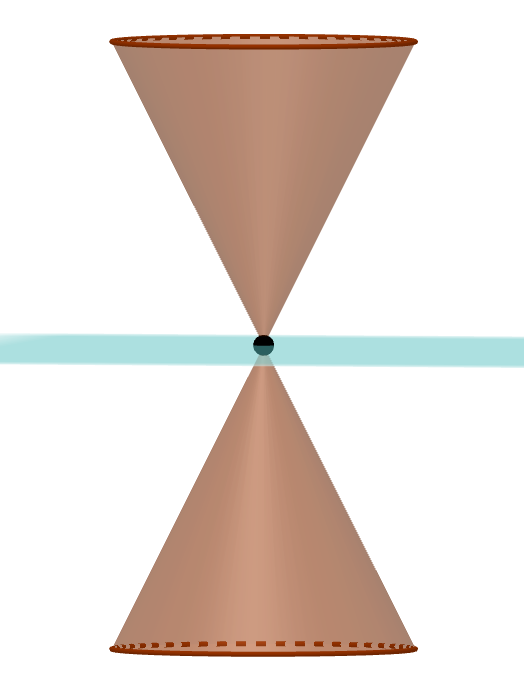
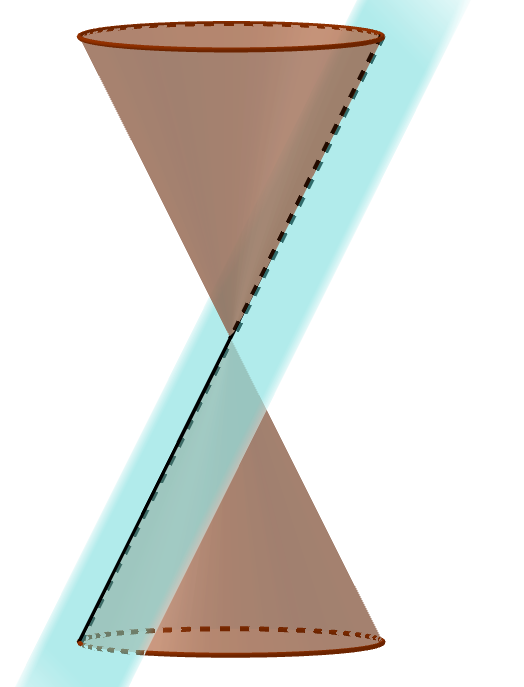
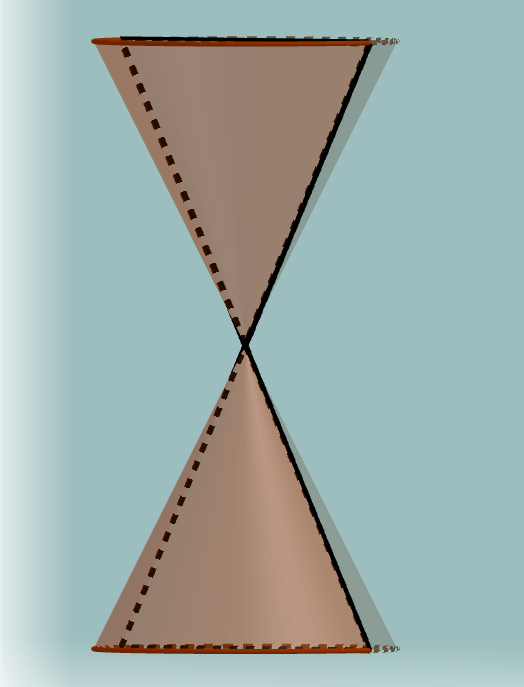
The point and lines are called degenerate conic sections because they do not produce curves. This unit deals mainly with the three major conic sections, but starts out by looking at the degenerate line.
Lines are described by the general equation Ax + By + C = 0 or, more commonly, by slope-intercept form y = mx + b where m is the slope and b is the y-intercept.
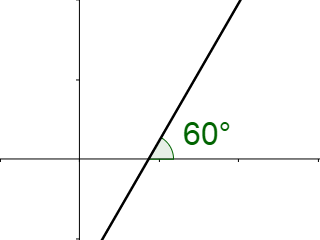
The inclination describes the steepness of a line. It is the angle the line makes with the positive x-axis.
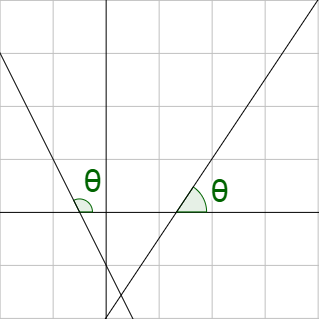
Since both slope and inclination describe the steepness of a line, they must be related. If a right angle is drawn on the line as in figure 3, the sides are x and y.
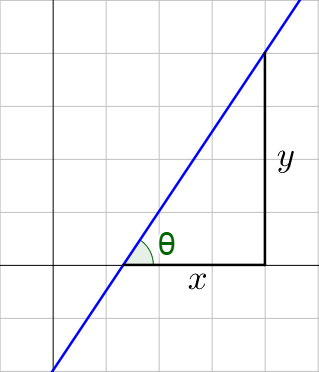
$$m=\frac{rise}{run}=\frac{y}{x}$$
Also,
$$\tan θ = \frac{opposite}{adjacent} = \frac{y}{x}$$
Since they both equal \(\frac{y}{x}\), set the slope and tangent equal to each other. This can be used to calculate the inclination of the line.
tan θ = m
where 0° < θ < 180°.
Remember that inverse tangent gives an angle between −90° and 90°. If you get a negative number when you solve for the inclination, add 180° because tangent has a period of 180°.
tan θ = m
where 0° < θ < 180° is the inclination and m = slope.
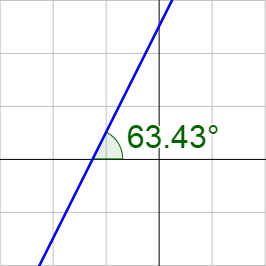
Find the inclination of 4x − 2y + 5 = 0.
Solution
First, find the slope by rewriting the equation in slope-intercept form.
4x − 2y + 5 = 0
−2y = −4x − 5
$$y=2x+\frac{5}{2}$$
So the slope is 2.
Now, find the inclination.
tan θ = 2
θ = tan−1 2 ≈ 63.4°
Find the inclination of x + 3y + 1 = 0.
Answer
161.6°
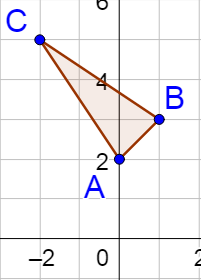
If two intersecting lines are drawn, an angle θ is formed at the intersection. That angle θ can be found using the inclinations of the lines.
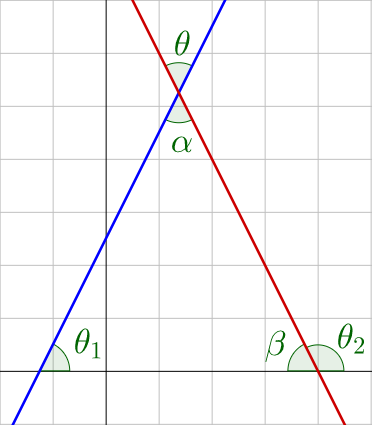
In figure 5, β + θ2 = 180° because they are a linear pair, so β = 180° − θ2. The sum of the three angles in a triangle is 180°, so
θ1 + α + β = 180°
α = 180° − θ1 − β
α = 180° − θ1 − (180° − θ2)
α = θ2 − θ1
α and θ are vertical angle, so they are congruent and the angle between two lines is
θ = θ2 − θ1
where 0° < θ < 90°.
This can be written with slopes. Take the tangent of both sides.
tan θ = tan(θ2 − θ1)
Use the difference formula for tangent.
$$\tan θ = \frac{\tan θ_2 - \tan θ_1}{1 + \tan θ_2 \tan θ_1}$$
Because the angles are inclinations, tan θ1 = m1 and tan θ2 = m2.
$$\tan θ = \left\lvert \frac{m_2 - m_1}{1 + m_1 m_2} \right\rvert$$
$$\tan θ = \left\lvert \frac{m_2 - m_1}{1 + m_1 m_2} \right\rvert$$
where 0° < θ < 90° is the angle between the lines and m1 and m2 are the slopes of the lines.
Find the angle between x − 2y = 0 and 3x + 2y − 1 = 0.
Solution
Begin by finding the slopes of the lines by rewriting them in slope-intercept form.
$$y = \frac{1}{2} x \text{ and } y = -\frac{3}{2} x + \frac{1}{2}$$
So the slopes are \(m_1 = \frac{1}{2}\) and \(m_2 = -\frac{3}{2}\).
Fill in the formula and find the angle.
$$\tan θ = \left\lvert \frac{m_2 - m_1}{1 + m_1 m_2} \right\rvert$$
$$\tan θ = \left\lvert \frac{-\frac{3}{2} - \frac{1}{2}}{1+\left(\frac{1}{2}\right)\left(-\frac{3}{2}\right)} \right\rvert$$
$$\tan θ = \left\lvert \frac{-4}{\frac{1}{4}} \right\rvert$$
$$\tan θ = 16$$
$$θ = 86.42°$$
Find the angle between 2x − 2y + 1 = 0 and x + y = 0.
Answer
90°
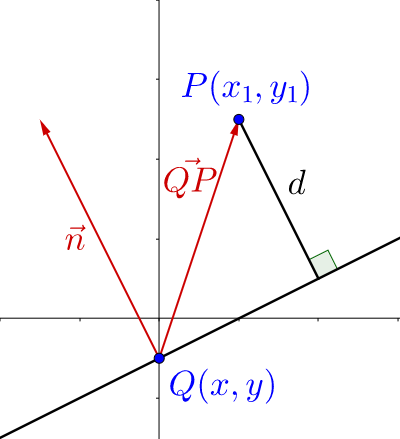
To find the distance from P to line Ax + By + C = 0, we can use vectors. Let \(P\left(x_1, y_1\right)\) be a point not on line Ax + By + C = 0. Let \(\overset{\rightharpoonup}{n} = \langle A, B \rangle\) be a perpendicular vector from point Q(x, y) on the line. The distance, d, between P and the line is the length of the orthogonal projection of \(\overset{\rightharpoonup}{QP}\) onto \(\overset{\rightharpoonup}{n}\).
$$proj_\overset{\rightharpoonup}{n} \overset{\rightharpoonup}{QP} = \frac{\overset{\rightharpoonup}{n} \cdot \overset{\rightharpoonup}{QP}}{\lVert \overset{\rightharpoonup}{n} \rVert}$$
This is slightly different than the formula from lesson 6-05. In this situation, we only want the length of the projection, so the direction unit vector \(\left(\frac{\overset{\rightharpoonup}{n}}{\lVert \overset{\rightharpoonup}{n} \rVert}\right)\) has not been included. Now, \(\overset{\rightharpoonup}{QP} = \langle x_1 - x, y_1 - y \rangle\), so
$$d = \left\lvert proj_\overset{\rightharpoonup}{n} \overset{\rightharpoonup}{QP} \right\rvert = \left\lvert \frac{A\left(x_1-x\right) + B\left(y_1-y\right)}{\sqrt{A^2 + B^2}} \right\rvert$$
$$=\frac{\lvert Ax_1 - Ax + By_1 - By \rvert}{\sqrt{A^2 + B^2}}$$
Because point \(Q\left(x, y\right)\) is on the line, Ax + By + C = 0, so C = −Ax − By.
$$d = \frac{\lvert Ax_1 + By_1 + C \rvert}{\sqrt{A^2 + B^2}}$$
$$d = \frac{\lvert Ax_1 + By_1 + C \rvert}{\sqrt{A^2 + B^2}}$$
where the point is P(x1, y1) and the line is Ax + By + C = 0.
Find the distance between the point (2, 5) and the line x + 3y − 2 = 0.
Solution
Fill in the distance formula with \(x_1 = 2\), \(y_1 = 5\), A = 1, B = 3, C = -2.
$$d = \frac{\lvert Ax_1 + By_1 + C \rvert}{\sqrt{A^2 + B^2}}$$
$$d = \frac{\lvert 1\left(2\right) + 3\left(5\right) + \left(-2\right) \rvert}{\sqrt{1^2 + 3^2}}$$
$$d = \frac{15}{\sqrt{10}} = \frac{3\sqrt{10}}{2}$$
Find the distance between the point (1, −2) and the line y = 2x − 1.
Answer
\(\frac{3\sqrt{5}}{5}\)
tan θ = m
where 0° < θ < 180° is the inclination and m = slope.
$$\tan θ = \left\lvert \frac{m_2 - m_1}{1 + m_1 m_2} \right\rvert$$
where 0° < θ < 90° is the angle between the lines and m1 and m2 are the slopes of the lines.
$$d = \frac{\lvert Ax_1 + By_1 + C \rvert}{\sqrt{A^2 + B^2}}$$
where the point is \(P\left(x_1, y_1\right)\) and the line is Ax + By + C = 0.
Helpful videos about this lesson.
