Precalculus by Richard Wright
Precalculus by Richard Wright
And he said: “Truly I tell you, unless you change and become like little children, you will never enter the kingdom of heaven. Therefore, whoever takes the lowly position of this child is the greatest in the kingdom of heaven.” Matthew 18:3-4 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.7.3
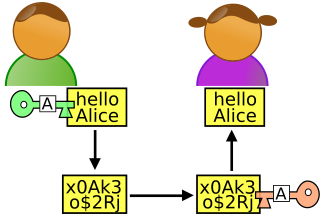
Cryptographers look for ways to encode messages so that if someone intercepts the message, then they cannot read it. This is important to protect private information on the internet or to send secret messages between government and military offices. One method called the Hill Cipher uses a matrix to encode and decode messages. But first, some applications of determinants.
Cramer's Rule uses determinants to solve a system of linear equations. Cramer's Rule is sometimes preferable to the other methods because Cramer's Rule can solve for one variable without solving for the others. For example, Cramer's Rule will let you find x without finding y or z.
To use Cramer's Rule to solve a system of linear equations
For a 2×2 system \(\left\{\begin{align} ax + by &= g \\ cx + dy &= h \end{align}\right.\)
$$ x = \frac{\left|\begin{matrix} \color{blue}{g} & b \\ \color{blue}{h} & d \end{matrix}\right|}{\left|\begin{matrix} a & b \\ c & d \end{matrix}\right|}; \quad y = \frac{\left|\begin{matrix} a & \color{blue}{g} \\ c & \color{blue}{h} \end{matrix}\right|}{\left|\begin{matrix} a & b \\ c & d \end{matrix}\right|} $$
For a 3×3 system \(\left\{\begin{align} ax + by + cz &= \ell \\ dx + ey + fz &= m \\ gx + hy + iz &= n \end{align}\right.\)
$$ x = \frac{\left|\begin{matrix} \color{blue}{\ell} & b & c \\ \color{blue}{m} & e & f \\ \color{blue}{n} & h & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|}; \quad y = \frac{\left|\begin{matrix} a & \color{blue}{\ell} & c \\ d & \color{blue}{m} & f \\ g & \color{blue}{n} & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|}; \quad z = \frac{\left|\begin{matrix} a & b & \color{blue}{\ell} \\ d & e & \color{blue}{m} \\ g & h & \color{blue}{n} \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|} $$
If the determinant of the coefficients (the denominator) is 0, then there are many solutions or no solution.
Use Cramer's Rule to solve \(\left\{\begin{alignat}{4} x &+& 2y &-& z &=& -1 \\ x &-& && 2z &=& -1 \\ && y &+& z &=& 1 \end{alignat}\right.\)
Solution
Set up Cramer's Rule for one of the variables such as x. The coefficients are the denominator and the numerator is the same except for the chosen variable column is replaced by the constants.
$$ x = \frac{\left|\begin{matrix} \color{blue}{\ell} & b & c \\ \color{blue}{m} & e & f \\ \color{blue}{n} & h & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|} $$
$$ x = \frac{\left|\begin{matrix} \color{blue}{-1} & 2 & -1 \\ \color{blue}{-1} & 0 & -2 \\ \color{blue}{1} & 1 & 1 \end{matrix}\right|}{\left|\begin{matrix} 1 & 2 & -1 \\ 1 & 0 & -2 \\ 0 & 1 & 1 \end{matrix}\right|} $$
$$ x = \require{cancel} \frac{ \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{-1}}} & \color{indigo}{\bcancel{\color{black}{2}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{-1}}}}} \\ -1 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{0}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{-2}}}}} \\ \color{red}{\cancel{\color{black}{1}}} & \color{orange}{\cancel{\color{black}{1}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{-1}}} & \color{green}{\cancel{\color{black}{2}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{-1}}}}} & 0 \\ \color{indigo}{\bcancel{\color{black}{1}}} & \color{purple}{\bcancel{\color{black}{1}}} \end{matrix} }{ \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{1}}} & \color{indigo}{\bcancel{\color{black}{2}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{-1}}}}} \\ 1 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{0}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{-2}}}}} \\ \color{red}{\cancel{\color{black}{0}}} & \color{orange}{\cancel{\color{black}{1}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{1}}} & \color{green}{\cancel{\color{black}{2}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} & 0 \\ \color{indigo}{\bcancel{\color{black}{0}}} & \color{purple}{\bcancel{\color{black}{1}}} \end{matrix} } $$
$$ x = \frac{ \color{blue}{(-1·0·1)} + \color{indigo}{(2·-2·1)} + \color{purple}{(-1·-1·1)} - \color{red}{(1·0·-1)} - \color{orange}{(1·-2·-1)} - \color{green}{(1·-1·2)} }{ \color{blue}{(1·0·1)} + \color{indigo}{(2·-2·0)} + \color{purple}{(-1·1·1)} - \color{red}{(0·0·-1)} - \color{orange}{(1·-2·1)} - \color{green}{(1·1·2)} } $$
$$ \require{enclose} x = \frac{-3}{-1} = \enclose{box}{3} $$
If you need to solve for more variables, set up the next one, y. In the first part, the denominator was already calculated, so that will be skipped in this step.
$$ y = \frac{\left|\begin{matrix} a & \color{blue}{\ell} & c \\ d & \color{blue}{m} & f \\ g & \color{blue}{n} & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|} $$
$$ y = \frac{\left|\begin{matrix} 1 & \color{blue}{-1} & -1 \\ 1 & \color{blue}{-1} & -2 \\ 0 & \color{blue}{1} & 1 \end{matrix}\right|}{\left|\begin{matrix} 1 & 2 & -1 \\ 1 & 0 & -2 \\ 0 & 1 & 1 \end{matrix}\right|} $$
$$ y = \require{cancel} \frac{ \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{1}}} & \color{indigo}{\bcancel{\color{black}{-1}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{-1}}}}} \\ 1 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{-1}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{-2}}}}} \\ \color{red}{\cancel{\color{black}{0}}} & \color{orange}{\cancel{\color{black}{1}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{1}}} & \color{green}{\cancel{\color{black}{-1}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} & -1 \\ \color{indigo}{\bcancel{\color{black}{0}}} & \color{purple}{\bcancel{\color{black}{1}}} \end{matrix} }{ -1 (\text{ from calculating } x) } $$
$$ y = \frac{ \color{blue}{(1·-1·1)} + \color{indigo}{(-1·-2·0)} + \color{purple}{(-1·1·1)} - \color{red}{(0·-1·-1)} - \color{orange}{(1·-2·1)} - \color{green}{(1·1·-1)} }{ -1 } $$
$$ \require{enclose} y = \frac{1}{-1} = \enclose{box}{-1} $$
Finally solve for z. In the first part, the denominator was already calculated, so that will be skipped in this step.
$$ z = \frac{\left|\begin{matrix} a & b & \color{blue}{\ell} \\ d & e & \color{blue}{m} \\ g & h & \color{blue}{n} \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|} $$
$$ z = \frac{\left|\begin{matrix} 1 & 2 & \color{blue}{-1} \\ 1 & 0 & \color{blue}{-1} \\ 0 & 1 & \color{blue}{1} \end{matrix}\right|}{\left|\begin{matrix} 1 & 2 & -1 \\ 1 & 0 & -2 \\ 0 & 1 & 1 \end{matrix}\right|} $$
$$ z = \require{cancel} \frac{ \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{1}}} & \color{indigo}{\bcancel{\color{black}{2}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{-1}}}}} \\ 1 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{0}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{-1}}}}} \\ \color{red}{\cancel{\color{black}{0}}} & \color{orange}{\cancel{\color{black}{1}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{1}}} & \color{green}{\cancel{\color{black}{2}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} & 0 \\ \color{indigo}{\bcancel{\color{black}{0}}} & \color{purple}{\bcancel{\color{black}{1}}} \end{matrix} }{ -1 \text{ from calculating } x } $$
$$ z = \frac{ \color{blue}{(1·0·1)} + \color{indigo}{(2·-1·0)} + \color{purple}{(-1·1·1)} - \color{red}{(0·0·-1)} - \color{orange}{(1·-1·1)} - \color{green}{(1·1·2)} }{ -1 } $$
$$ \require{enclose} z = \frac{-2}{-1} = \enclose{box}{2} $$
So the solution, (3, −1, 2), is found by simply finding four determinants.
Solve using Cramer's Rule \(\left\{\begin{align} 2x - y &= 8 \\ -3x + 4y &= -17 \end{align}\right.\)
Answer
(3, −2)
The area of a triangle can be found with using \(\frac{1}{2} bh\) if you know the base and height or Heron's formula if you know the lengths of all the sides. But what if only the coordinates of the vertices are known. One way is to use the distance formula to find the side lengths and then Heron's formula, but that would be long. It turns out a simple determinant will give you the area of the triangle.
The area of a triangle with vertices (x1, y1), (x2, y2), (x3, y3)
$$ Area = ±\frac{1}{2} \left|\begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{matrix}\right| $$
Where the + or − is chosen to make the area positive.
Find the area of the triangle with vertices (2, −3), (4, 2), and (−1, 1).
Solution
Fill in the formula with the vertices. The order of the vertices does not matter.
$$ Area = ±\frac{1}{2} \left|\begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{matrix}\right| $$
$$ Area = ±\frac{1}{2} \left|\begin{matrix} 2 & -3 & 1 \\ 4 & 2 & 1 \\ -1 & 1 & 1 \end{matrix}\right| $$
$$ \require{cancel} Area = ±\frac{1}{2} \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{2}}} & \color{indigo}{\bcancel{\color{black}{-3}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{1}}}}} \\ 4 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{2}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{1}}}}} \\ \color{red}{\cancel{\color{black}{-1}}} & \color{orange}{\cancel{\color{black}{1}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{2}}} & \color{green}{\cancel{\color{black}{-3}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{4}}}}} & 2 \\ \color{indigo}{\bcancel{\color{black}{-1}}} & \color{purple}{\bcancel{\color{black}{1}}} \end{matrix} $$
$$ Area = ±\frac{1}{2} \left(\color{blue}{(2·2·1)} + \color{indigo}{(-3·1·-1)} + \color{purple}{(1·4·1)} - \color{red}{(-1·2·1)} - \color{orange}{(1·1·2)} - \color{green}{(1·4·-3)}\right) $$
$$ Area = \frac{23}{2} $$
The determinant was 23, and because that was positive we chose the + from the ± to make the area positive. If the determinant was negative, we would have chosen the − to make the area positive.
Find the area of the triangle with vertices (−1, −2), (5, 1), and (2, 6).
Answer
\(\frac{39}{2}\)
Three points in a plane form a triangle unless they are in a straight line. If the three points form a straight line, then the area of the "triangle" formed by the points is 0. Using the area of a triangle determinant, collinearness of points and equations of lines can be found. Because the area of lines is 0, the \(±\frac{1}{2}\) is not needed in the following formulas.
Three points are collinear if the area of the triangle formed is 0.
If \(\left|\begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{matrix}\right| = 0\), then the points are collinear.
To find the equation of a line given 2 points (x1, y1) and (x2, y2), substitute the points and simplify
$$ \left|\begin{matrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \end{matrix}\right| = 0 $$
Find the equation of the line passing through (3, 1) and (−2, 4).
Solution
Fill the points into the determinant. x and y stay as variables.
$$ \left|\begin{matrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \end{matrix}\right| = 0 $$
$$ \left|\begin{matrix} x & y & 1 \\ 3 & 1 & 1 \\ -2 & 4 & 1 \end{matrix}\right| = 0 $$
Calculate the determinant.
$$ \require{cancel} \left|\begin{matrix} \color{blue}{\bcancel{\color{black}{x}}} & \color{indigo}{\bcancel{\color{black}{y}}} & \color{purple}{\bcancel{\color{red}{\cancel{\color{black}{1}}}}} \\ 3 & \color{blue}{\bcancel{\color{red}{\cancel{\color{black}{1}}}}} & \color{indigo}{\bcancel{\color{orange}{\cancel{\color{black}{1}}}}} \\ \color{red}{\cancel{\color{black}{-2}}} & \color{orange}{\cancel{\color{black}{4}}} & \color{blue}{\bcancel{\color{green}{\cancel{\color{black}{1}}}}} \end{matrix}\right| \begin{matrix} \color{orange}{\cancel{\color{black}{x}}} & \color{green}{\cancel{\color{black}{y}}} \\ \color{purple}{\bcancel{\color{green}{\cancel{\color{black}{3}}}}} & 1 \\ \color{indigo}{\bcancel{\color{black}{-2}}} & \color{purple}{\bcancel{\color{black}{4}}} \end{matrix} = 0 $$
(x·1·1) + (y·1·−2) + (1·3·4) − (−2·1·1) − (4·1·x) − (1·3·y) = 0
x + (−2y) + 12 − (−2) − 4x − 3y = 0
Rearrange the terms into an equation of a line.
−3x − 5y + 14 = 0
3x + 5y = 14
Find the equation of the line passing through (−2, −4) and (3, 2).
Answer
6x − 5y = 8
There are many reasons to want to send secret messages. One of the most adventurous is spies sending messages back and forth to their handlers. Or another use might be a young man using a code to ask a young lady out to the spring banquet. One method of encoding messages, the Hill Cipher, uses matrix multiplication. Even though the Hill Cipher looks complicated, it is no longer used politically or commercially because it is linear and thus easy to break if a few letters of the message are known.
| _ = 0 | I = 9 | R = 18 |
| A = 1 | J = 10 | S = 19 |
| B = 2 | K = 11 | T = 20 |
| C = 3 | L = 12 | U = 21 |
| D = 4 | M = 13 | V = 22 |
| E = 5 | N = 14 | W = 23 |
| F = 6 | O = 15 | X = 24 |
| G = 7 | P = 16 | Y = 25 |
| H = 8 | Q = 17 | Z = 26 |
Multiply the numbers of the encoded message with the inverse of the encoding matrix
Encode the message SMILE using the encoding matrix \(\left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right]\).
Solution
Change the letters into numbers.
| S | M | I | L | E |
| 19 | 13 | 9 | 12 | 5 |
Group the numbers into 1×2 matrices because the encoding matrix is 2×2. There are only five numbers so a 0 for space will be added onto the end.
[19 13] [9 12] [5 0]
Multiply each matrix with encoding matrix.
$$ \color{blue}{\left[\begin{matrix} 19 & 13 \end{matrix}\right]} \left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right] = \left[\begin{matrix} 83 & -7 \end{matrix}\right] $$
$$ \color{red}{\left[\begin{matrix} 9 & 12 \end{matrix}\right]} \left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right] = \left[\begin{matrix} 51 & -15 \end{matrix}\right] $$
$$ \color{purple}{\left[\begin{matrix} 5 & 0 \end{matrix}\right]} \left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right] = \left[\begin{matrix} 15 & 10 \end{matrix}\right] $$
The encoded message is 83, −7, 51, −15, 15, 10
Decode the message 27, −15, 64, 0, 51, -31 using the inverse of \(\left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right]\).
Solution
Start by finding the inverse of the encoding matrix to form the decoding matrix.
$$ \left[\begin{matrix} 3 & 1 \\ 2 & -2 \end{matrix}\right]^{-1} = \frac{1}{3(-2) - 2(1)} \left[\begin{matrix} -2 & -1 \\ -2 & 3 \end{matrix}\right] $$
$$ = \left[\begin{matrix} \frac{1}{4} & \frac{1}{8} \\ \frac{1}{4} & -\frac{3}{8} \end{matrix}\right] $$
Group the message numbers into 1×2 matrices because the encoding matrix is 2×2.
[27 −15], [64 0], [51 -31]
Multiply the matrices with the decoding matrix.
$$ \color{blue}{\left[\begin{matrix} 27 & -15 \end{matrix}\right]} \left[\begin{matrix} \frac{1}{4} & \frac{1}{8} \\ \frac{1}{4} & -\frac{3}{8} \end{matrix}\right] = \left[\begin{matrix} 3 & 9 \end{matrix}\right] $$
$$ \color{red}{\left[\begin{matrix} 64 & 0 \end{matrix}\right]} \left[\begin{matrix} \frac{1}{4} & \frac{1}{8} \\ \frac{1}{4} & -\frac{3}{8} \end{matrix}\right] = \left[\begin{matrix} 16 & 8 \end{matrix}\right] $$
$$ \color{purple}{\left[\begin{matrix} 51 & -31 \end{matrix}\right]} \left[\begin{matrix} \frac{1}{4} & \frac{1}{8} \\ \frac{1}{4} & -\frac{3}{8} \end{matrix}\right] = \left[\begin{matrix} 5 & 18 \end{matrix}\right] $$
The decoded numbers are 3, 9, 16, 8, 5, 18. Convert these into numbers into letters, CIPHER.
Encode the message GOOD DAY using the encoding matrix \(\left[\begin{matrix} -1 & 2 \\ -3 & 1 \end{matrix}\right]\).
Answer
−52, 29, −27, 34, −12, 4, −76, 27
To use Cramer's Rule to solve a system of linear equations
For a 2×2 system \(\left\{\begin{align} ax + by &= g \\ cx + dy &= h \end{align}\right.\)
$$ x = \frac{\left|\begin{matrix} \color{blue}{g} & b \\ \color{blue}{h} & d \end{matrix}\right|}{\left|\begin{matrix} a & b \\ c & d \end{matrix}\right|}; \quad y = \frac{\left|\begin{matrix} a & \color{blue}{g} \\ c & \color{blue}{h} \end{matrix}\right|}{\left|\begin{matrix} a & b \\ c & d \end{matrix}\right|} $$
For a 3×3 system \(\left\{\begin{align} ax + by + cz &= \ell \\ dx + ey + fz &= m \\ gx + hy + iz &= n \end{align}\right.\)
$$ x = \frac{\left|\begin{matrix} \color{blue}{\ell} & b & c \\ \color{blue}{m} & e & f \\ \color{blue}{n} & h & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|}; \quad y = \frac{\left|\begin{matrix} a & \color{blue}{\ell} & c \\ d & \color{blue}{m} & f \\ g & \color{blue}{n} & i \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|}; \quad z = \frac{\left|\begin{matrix} a & b & \color{blue}{\ell} \\ d & e & \color{blue}{m} \\ g & h & \color{blue}{n} \end{matrix}\right|}{\left|\begin{matrix} a & b & c \\ d & e & f \\ g & h & i \end{matrix}\right|} $$
If the determinant of the coefficients (the denominator) is 0, then there are many solutions or no solution.
The area of a triangle with vertices (x1, y1), (x2, y2), (x3, y3)
$$ Area = ±\frac{1}{2} \left|\begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{matrix}\right| $$
Where the + or − is chosen to make the area positive.
Three points are collinear if the area of the triangle formed is 0.
If \(\left|\begin{matrix} x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \\ x_3 & y_3 & 1 \end{matrix}\right| = 0\), then the points are collinear.
To find the equation of a line given 2 points (x1, y1) and (x2, y2), substitute the points and simplify
$$ \left|\begin{matrix} x & y & 1 \\ x_1 & y_1 & 1 \\ x_2 & y_2 & 1 \end{matrix}\right| = 0 $$
| _ = 0 | I = 9 | R = 18 |
| A = 1 | J = 10 | S = 19 |
| B = 2 | K = 11 | T = 20 |
| C = 3 | L = 12 | U = 21 |
| D = 4 | M = 13 | V = 22 |
| E = 5 | N = 14 | W = 23 |
| F = 6 | O = 15 | X = 24 |
| G = 7 | P = 16 | Y = 25 |
| H = 8 | Q = 17 | Z = 26 |
Multiply the numbers of the encoded message with the inverse of the encoding matrix
Helpful videos about this lesson.