Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Through him all things were made; without him nothing was made that has been made. In him was life, and that life was the light of all mankind. The light shines in the darkness, and the darkness has not overcome it. John 1:3-5 NIV

11-01 3-D Coordinate System

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.3

3-D shapes
Three dimensional shapes (sphere, pyramid, and cone). (RW)

Much of what has been done so far in your mathematics experience has been in two dimensions. There has only been x and y. However, there are more dimensions. We can move freely in three dimensions in our universe. This chapter is about three dimensional shapes. By finding patterns two- and three-dimensions, it is possible to think of higher dimensions. In mathematics, there can be any number of dimensions. Each dimension is identified by a separate variable.

Three-Dimensional Coordinate System

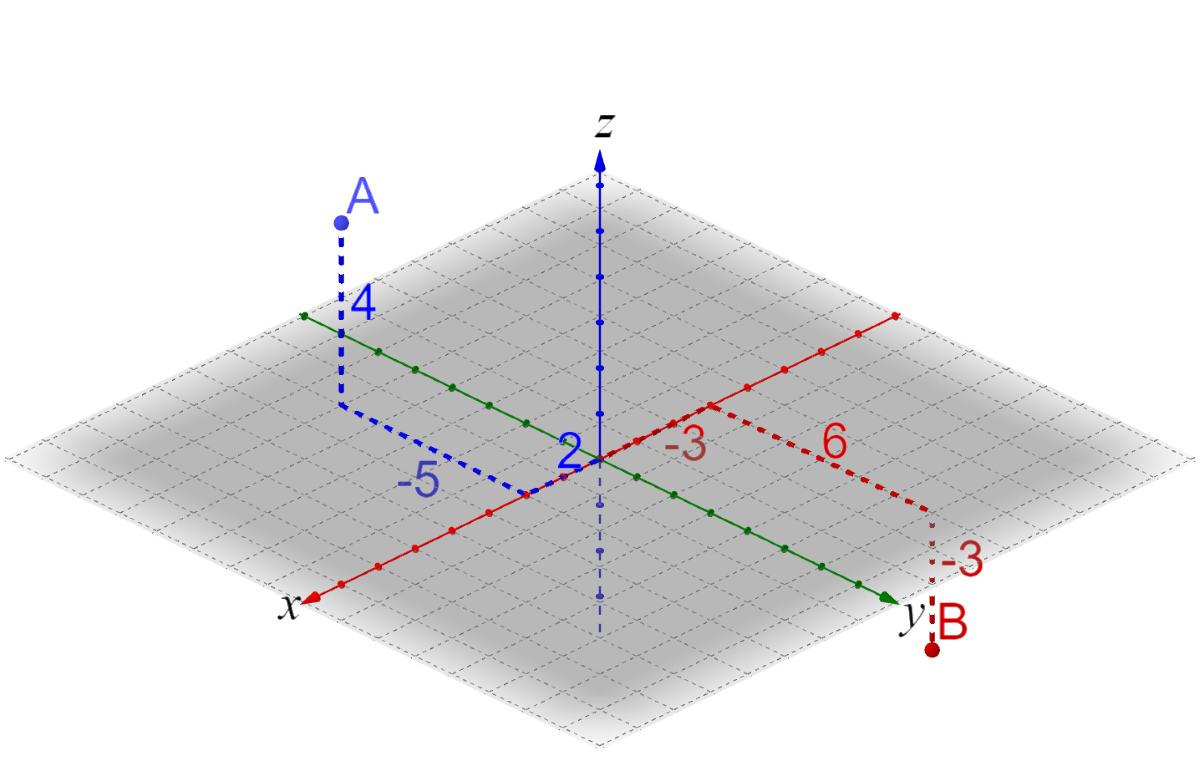
Points in two dimensions are described by the ordered pair (x, y). Points in three dimensions are described by the ordered triple (x, y, z). There are a couple standard ways to graph points in three dimensions. The method this book uses is with the positive x-axis coming diagonally down to the left, the positive y-axis going diagonally down to the right, and the positive z-axis going up. In reality, the x and y-axes are coming out of the paper at an angle. The view of the graph is looking down at the origin. No matter how you graph three-dimensions, it will always be a projection since the graph will be drawn on two-dimensional paper. Thus, you have to imagine what the graph really looks like.

3-D coordinate system
Three dimensional coordinate system.
3-D coordinate system
Three dimensional coordinate system.

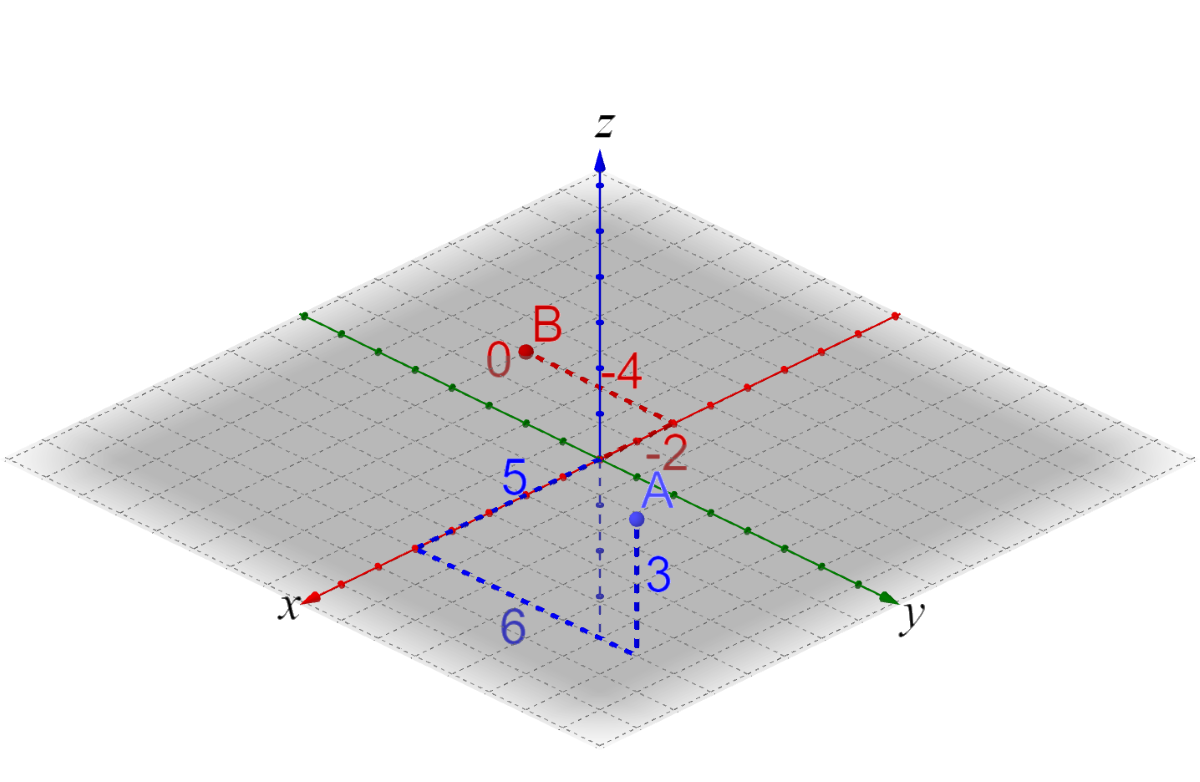
Graph points by moving out along the x-axis, then over along the y-axis, and up the z-axis. It is helpful to use grid paper.

3-Dimensional Coordinates

Graph by

  1. Move along x-axis
  2. Move along y-axis
  3. Move up or down along the z-axis

Graph 3D Points

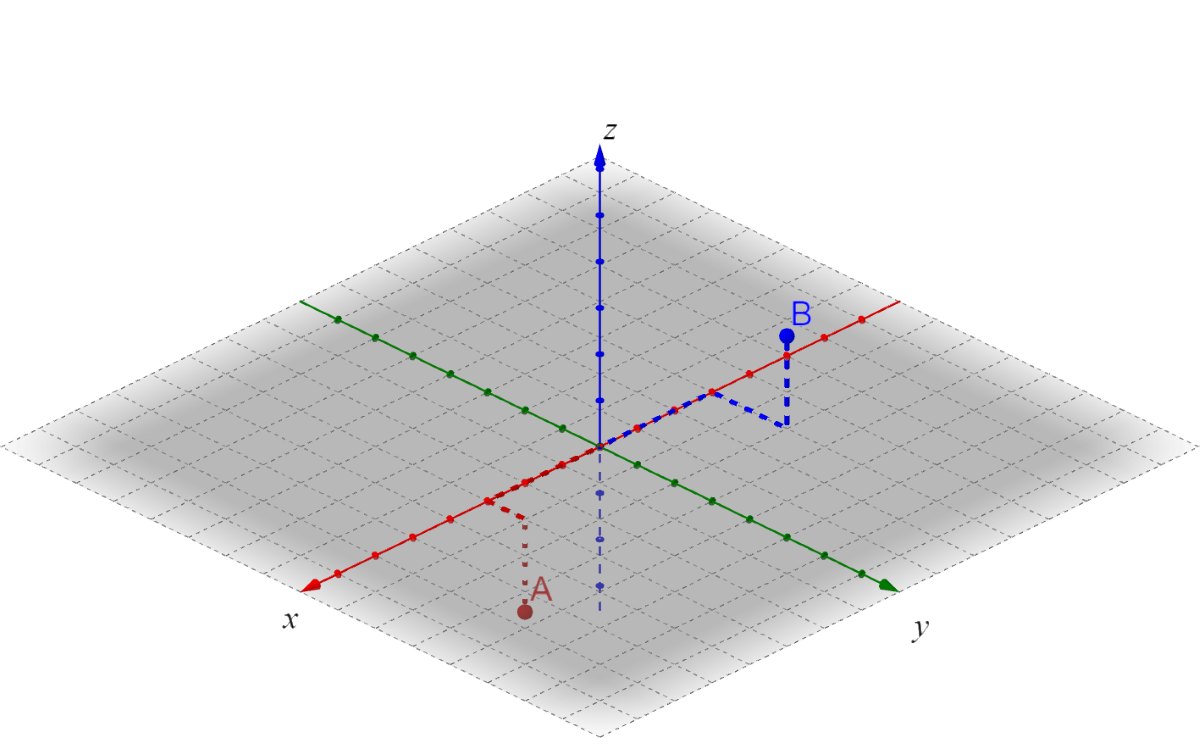
Graph A(5, 6, 3) and B(–2, –4, 0)

Solution

  1. Move along x-axis
  2. Move along y-axis
  3. Move up or down along the z-axis
3-D points
3D Points.

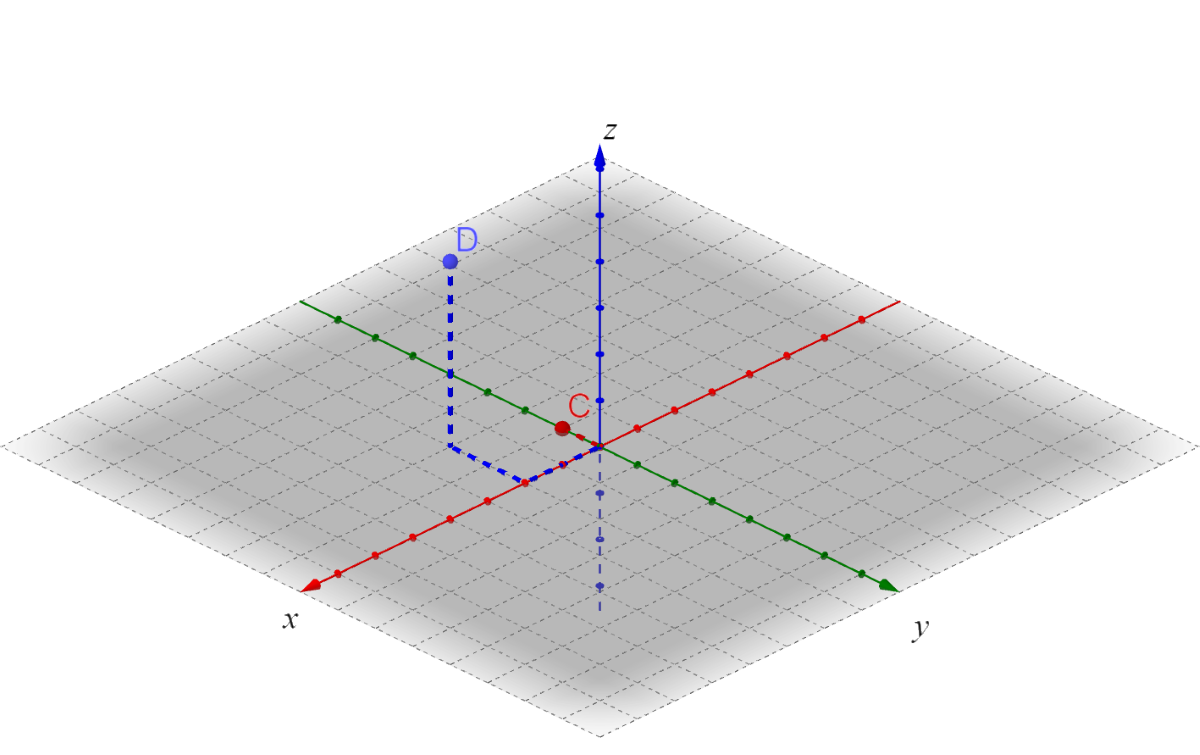
Graph A(2, –5, 4) and B(–3, 6, –3)

Answer

3-D points

Distance and Midpoint Formulas

The distance and midpoint formulas in three dimensions are just extensions of two dimensions. The distance formula in two dimensions comes from the Pythagorean Theorem. In three dimensions, the Pythagorean Theorem has to be used twice: first in the xy-plane with just the x- and y-coordinates, then with that distance and the distance the z-coordinate is above the plane. This produces

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$

In two dimensions, the midpoint formula is the average or arithmetic mean of the two endpoints of the segment. This is still true in three dimensions.

$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\right) $$

Distance Formula

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$

Midpoint Formula

$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\right) $$

Distance and Midpoint

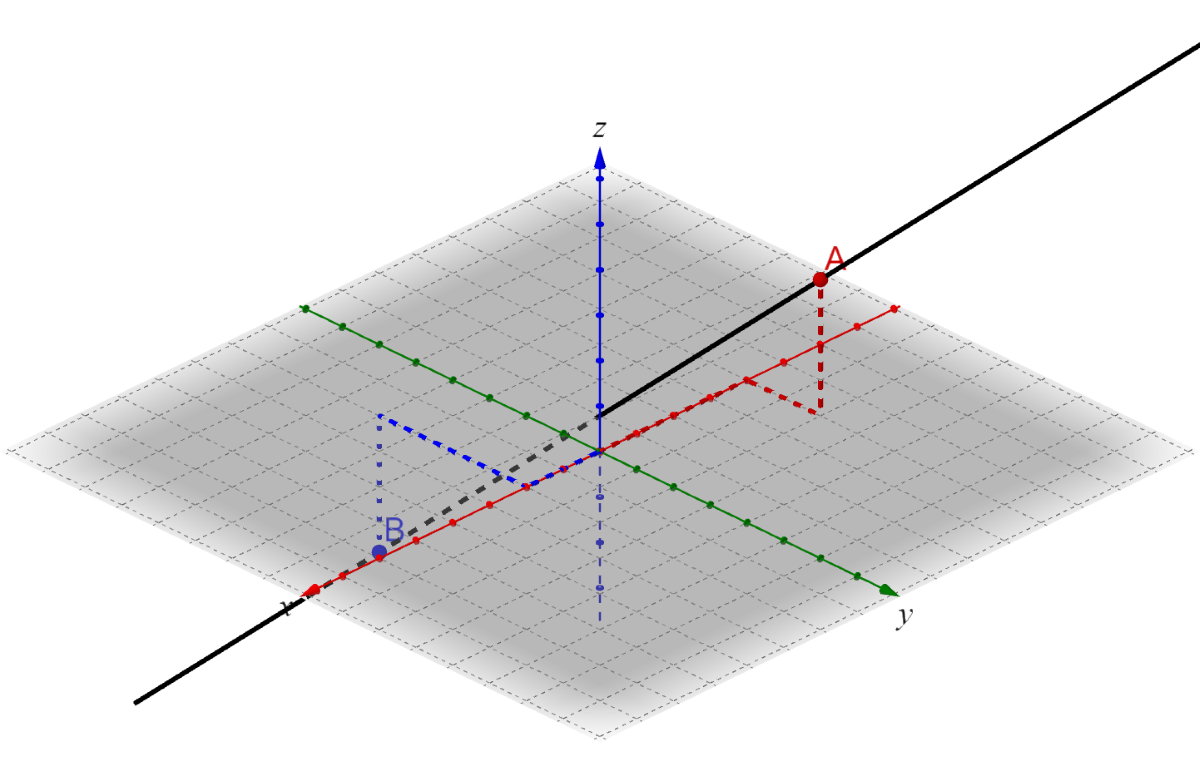
Find the (a) distance and (b) midpoint between A(2, 4, –6) and B(–4, 3, 2).

Solution

  1. The first point, A(2, 4, –6), is (x1, y1, z1) and the second point, B(–4, 3, 2), is (x2, y2, z2). Substitute those points into the distance formula and evaluate.

    $$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$

    $$ AB = \sqrt{(-4 - 2)^2 + (3 - 4)^2 + (2 - (-6))^2} $$

    $$ AB = \sqrt{(-6)^2 + 1^2 + 8^2} $$

    $$ AB = \sqrt{36 + 1 + 64} $$

    $$ AB = \sqrt{101} ≈ 10.05 $$

  2. The first point, A(2, 4, –6), is (x1, y1, z1) and the second point, B(–4, 3, 2), is (x2, y2, z2). Substitute those points into the midpoint formula and evaluate.

    $$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\right) $$

    $$ Midpoint = \left(\frac{2 + (-4)}{2}, \frac{4 + 3}{2}, \frac{(-6) + 2}{2}\right) $$

    $$ Midpoint = \left(-1, \frac{7}{2}, -2\right) $$

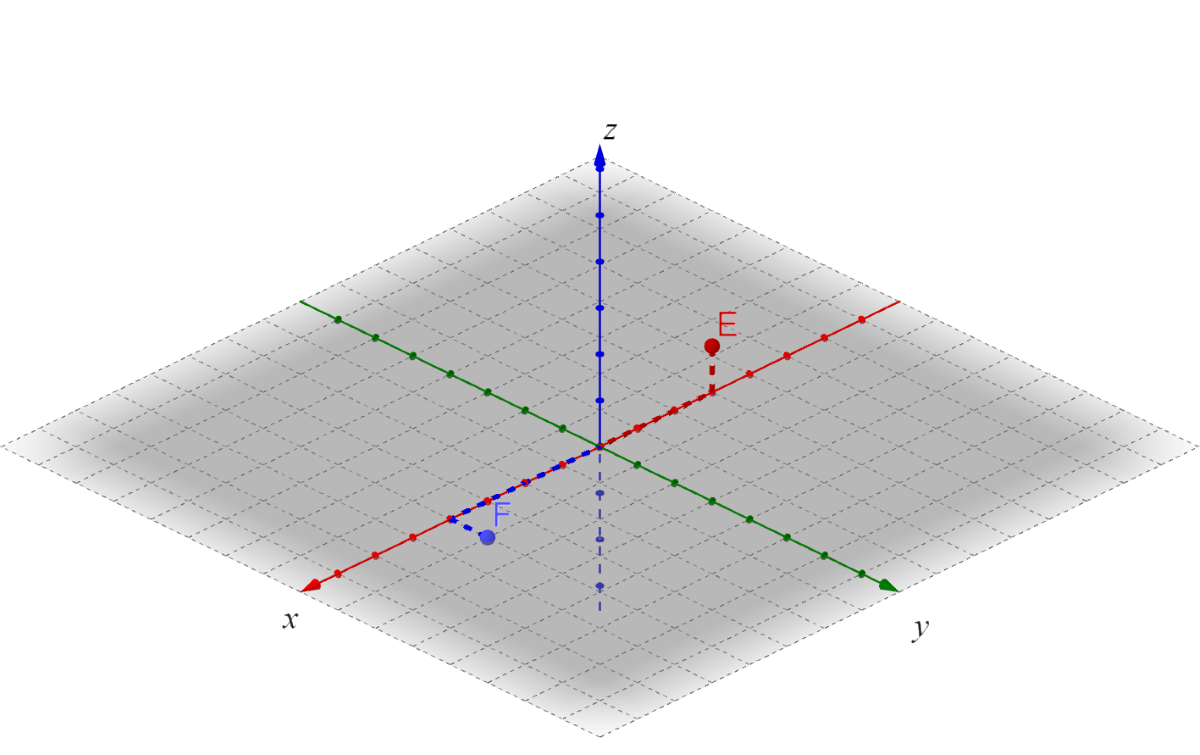
Find the (a) distance and (b) midpoint between C(7, –2, 1) and B(0, 1, 5).

Answer

\(\sqrt{74} ≈ 8.60; \left(\frac{7}{2}, -\frac{1}{2}, 3\right)\)

Equation of a Sphere

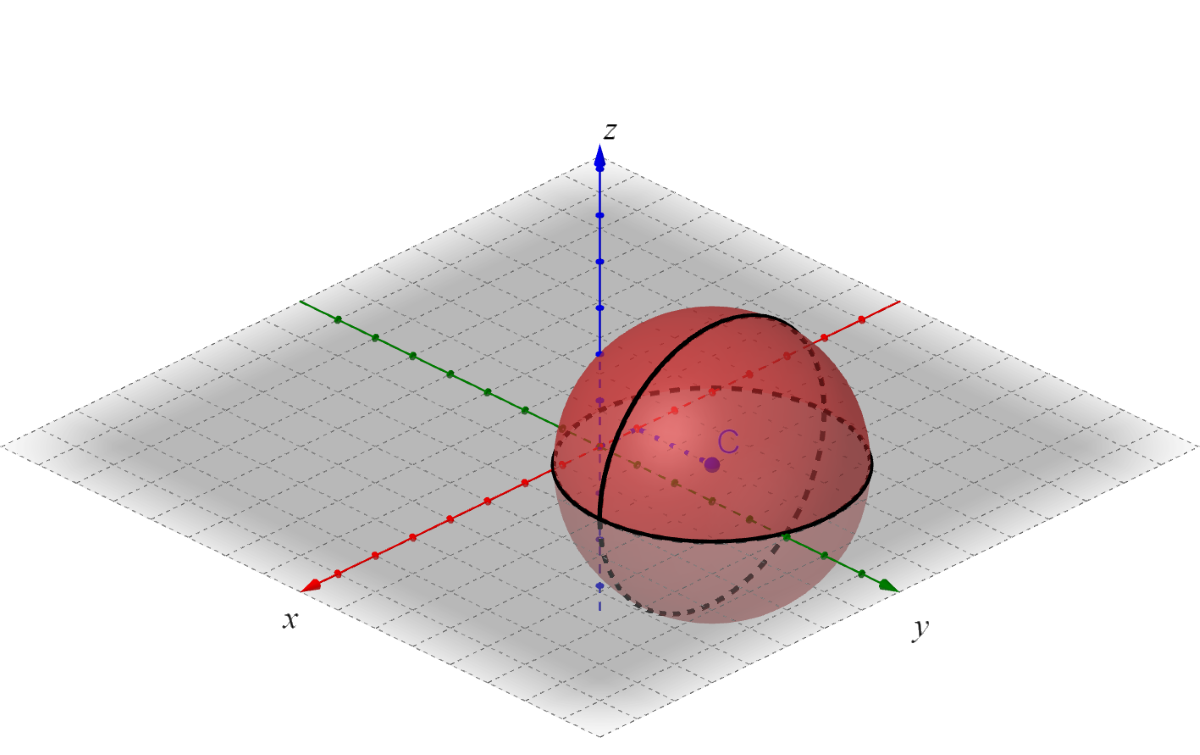
In two dimensions, a circle is all the points a given distance from the central point, and its equation is (x − h)2 + (y − k)2 = r2 where (h, k) is the center and r is the radius. In three dimensions, all the points a given distance from the central point is a sphere, and its equation is (x − h)2 + (y − k)2 + (z − k)2 = r2 where (h, k, j) is the center and r is the radius.

Graph a sphere by plotting the center and going every direction the distance of the radius. Usually two or three circles are drawn to represent the sphere.

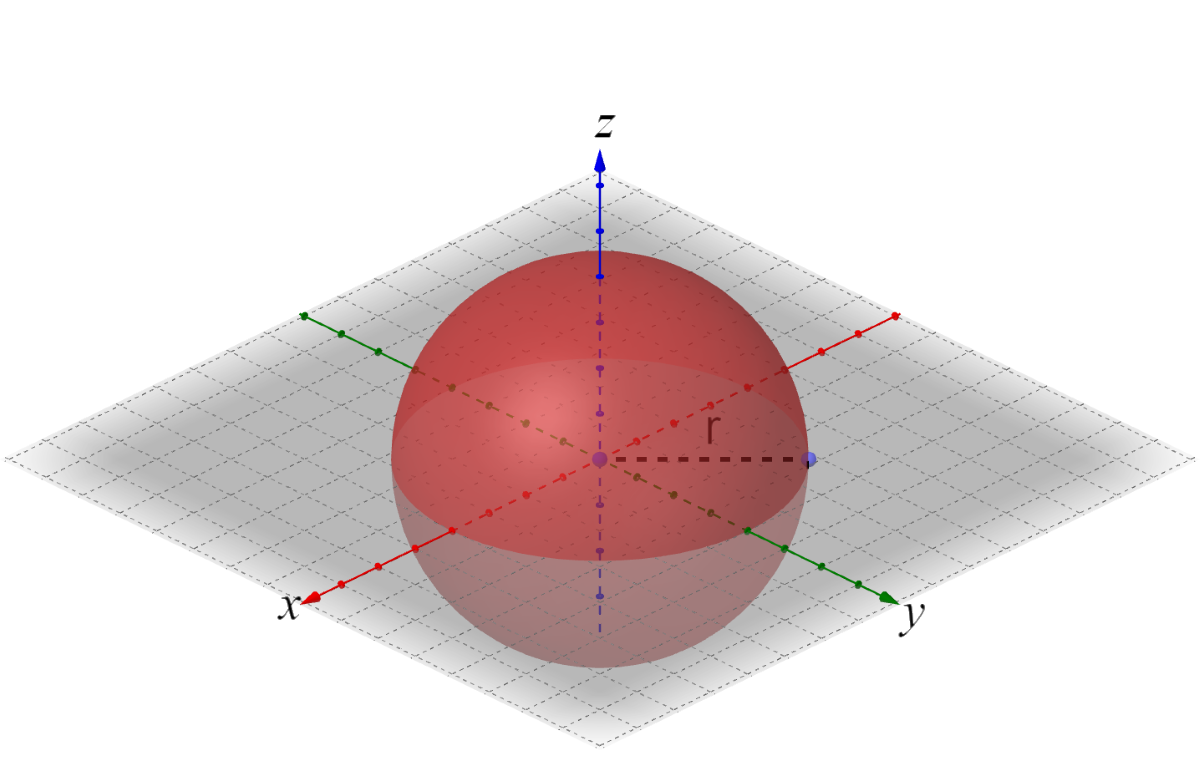
sphere
Sphere.
Equation of a Sphere

(x − h)2 + (y − k)2 + (z − j)2 = r2

where (h, k, j) is the center and r is the radius.

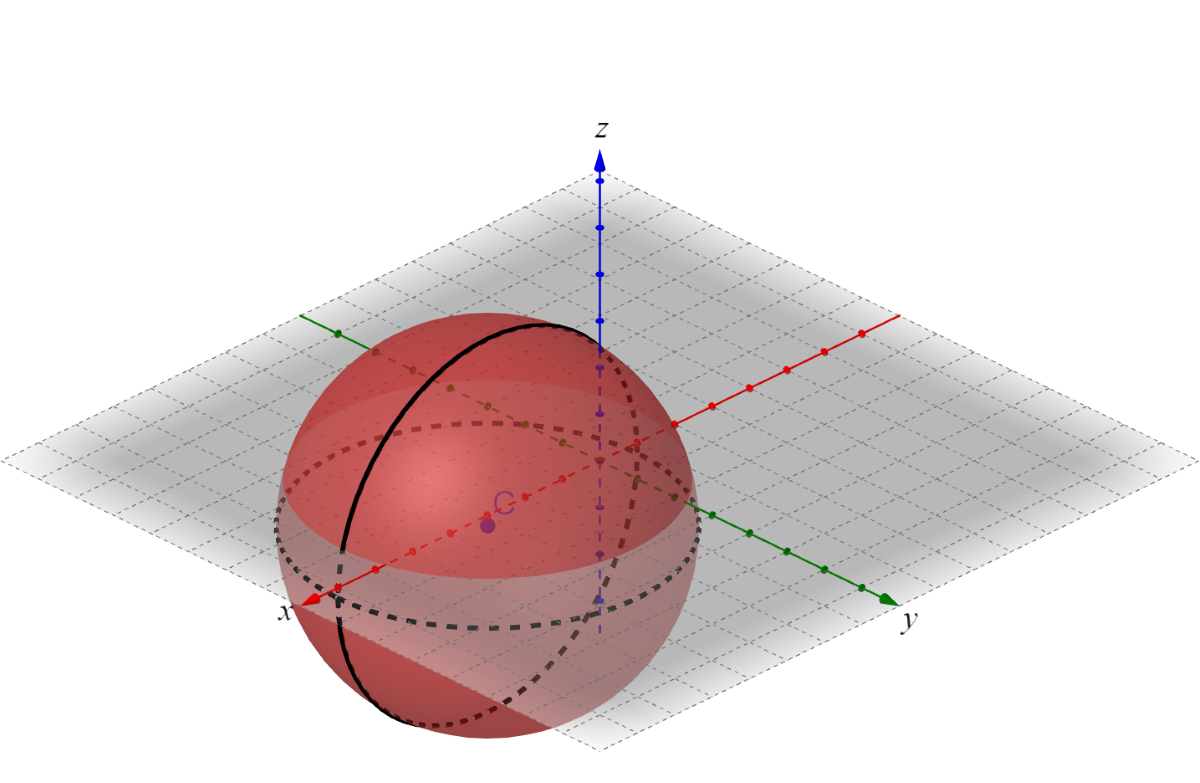
Graph a Sphere
  1. Plot the center.
  2. Plot a point the distance of the radius from the center in every direction.
  3. Usually draw two or three circles to represent the sphere.

Graph a Sphere

Graph (x − 2)2 + (y + 1)2 + (z + 1)2 = 16

Solution

Compare the equation to (x − h)2 + (y − k)2 + (z − k)2 = r2 to find the center and radius. The center is (h, k, j) which is (2, –1, –1) for this equation. r2 is 16, so r = 4.

Graph the center and move each direction the distance of the radius, 4.

sphere
(x − 2)2 + (y + 1)2 + (z + 1)2 = 16

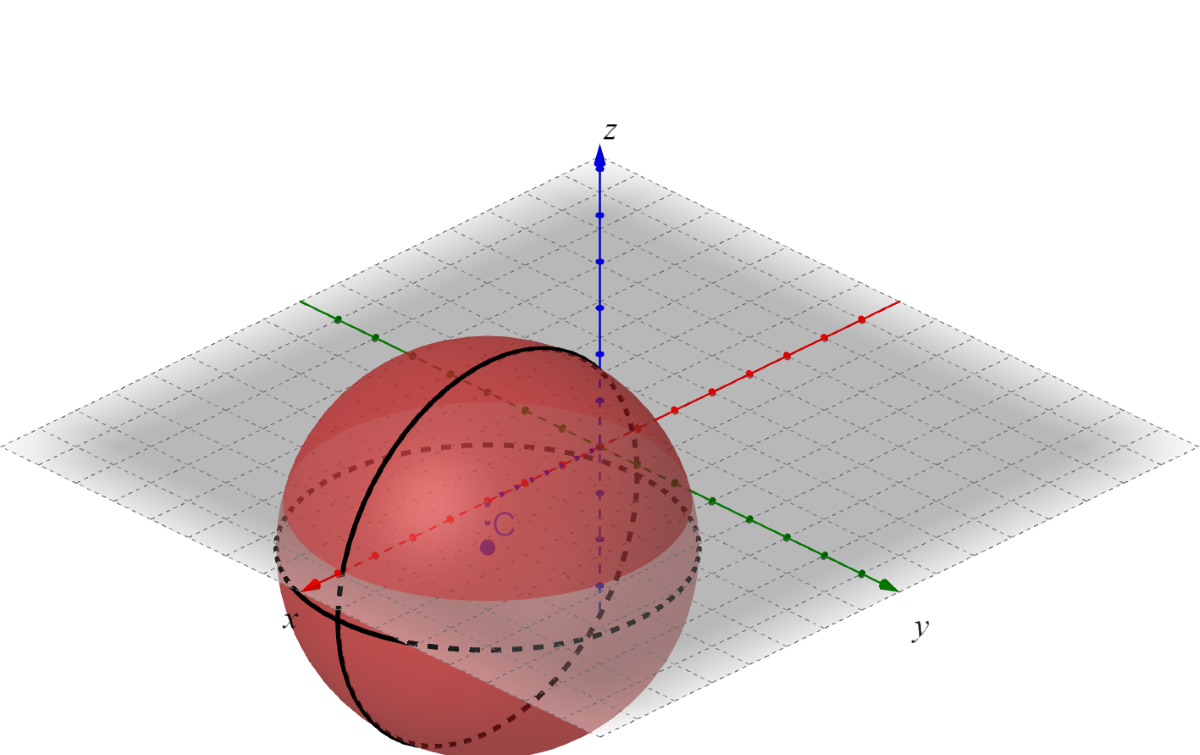
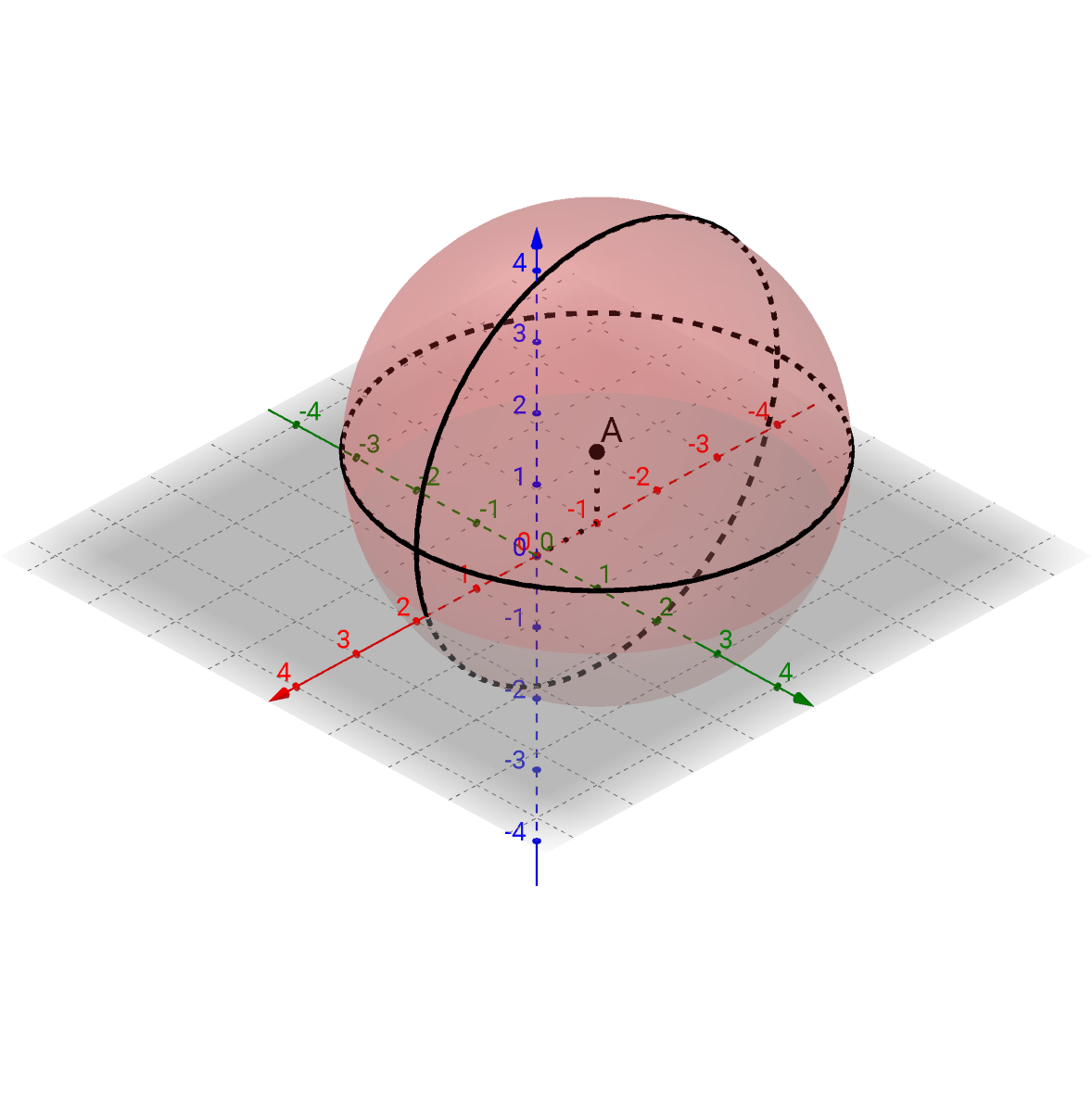
Graph (x + 1)2 + y2 + (z − 1)2 = 9

Answer

Lesson Summary
3-Dimensional Coordinates

Graph by

  1. Move along x-axis
  2. Move along y-axis
  3. Move up or down along the z-axis
Distance Formula

$$ d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} $$

Midpoint Formula

$$ Midpoint = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2}\right) $$

Equation of a Sphere

(x − h)2 + (y − k)2 + (z − j)2 = r2

where (h, k, j) is the center and r is the radius.

Graph a Sphere
  1. Plot the center.
  2. Plot a point the distance of the radius from the center in every direction.
  3. Usually draw two or three circles to represent the sphere.

Helpful videos about this lesson.

Practice Exercises

  1. Graph the following points.
  2. A(3, 1, −2) and B(−3, 2, 2)
  3. C(0, −1, 0) and D(2, −2, 4)
  4. E(−3, 0, 1) and F(4, 1, 0)
  5. Graph the line passing through (−4, 2, 3) and (2, −4, −3).
  6. Find the distance between the two points.
  7. A(3, 1, −2) and B(−3, 2, 2)
  8. C(0, −1, 0) and D(2, −2, 4)
  9. E(−3, 0, 1) and F(4, 1, 0)
  10. Find the midpoint between the two points.
  11. A(3, 1, −2) and B(−3, 2, 2)
  12. C(0, −1, 0) and D(2, −2, 4)
  13. E(−3, 0, 1) and F(4, 1, 0)
  14. Write the equation of the sphere with the given properties.
  15. Center at (2, −3, 1) and radius 5
  16. Center at (0, 2, −1) and a point on the sphere is (2, 3, 4)
  17. The ends of the diameter are at (−1, 4, 0) and (3, 8, −6).
  18. Graph the sphere.
  19. (x + 1)2 + (y − 2)2 + z2 = 9
  20. (x − 3)2 + y2 + (z + 1)2 = 16
  21. Mixed Review
  22. (10-08) What is the probability of randomly guessing the correct answers on a 5 question true/false quiz?
  23. (10-07) You have 16 model ships to display on a shelf. How many different orders can you display 10 of them because that is all the space you have on the shelf?
  24. (10-02) Evaluate \(\displaystyle \sum_{i=1}^{20} (i^3+i)\).
  25. (6-05) Evaluate ⟨3, 4⟩ · ⟨-2, 2⟩.
  26. (6-03) Given \(\overset{\rightharpoonup}{m} = \langle 2,-3 \rangle\) and \(\overset{\rightharpoonup}{n} = \langle -1, 6 \rangle\), find \(2\overset{\rightharpoonup}{m} + \overset{\rightharpoonup}{n}\).

Answers

  5. \(\sqrt{53}\)
  6. \(\sqrt{21}\)
  7. \(\sqrt{51}\)
  8. \(\left(0, \frac{3}{2}, 0\right)\)
  9. \(\left(1, -\frac{3}{2}, 2\right)\)
  10. \(\left(\frac{1}{2}, \frac{1}{2}, \frac{1}{2}\right)\)
  11. (x − 2)2 + (y + 3)2 + (z − 1)2 = 25
  12. x2 + (y − 2)2 + (z + 1)2 = 30
  13. (x − 1)2 + (y − 6)2 + (z + 3)2 = 17
  16. 0.03125
  17. 2.91×1010
  18. 44310
  19. 2
  20. ⟨3, 0⟩