Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
“He himself bore our sins” in his body on the cross, so that we might die to sins and live for righteousness; “by his wounds you have been healed.” 1 Peter 2:24 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.3, PC.6.4
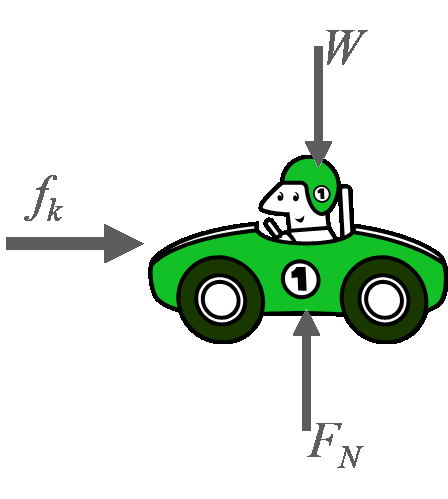
In physics, some measurements have direction as an important part of the measurement, such as forces. It is important which direction a force is applied. Measurements with direction are called vectors, and forces are vectors. To solve force problems, the forces acting on an object are drawn on a freebody diagram as in figure 1. The force vectors are then added together. This lesson will explore how to do vector operations such as vector addition.
Vectors in two dimensions are written in component form like
$$ \overset{\rightharpoonup}{v} = \langle v_1, v_2 \rangle $$
Vectors in three dimensions are written similarly with z included.
$$ \overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle $$
To find the component form of a vector from the initial point (p1, p2, p3) to the terminal point (q1, q2, q3), subtract the corresponding coordinates. This will give the distance in each component direction.
$$ \overset{\rightharpoonup}{v} = \langle q_1 - p_1, q_2 - p_2, q_3 - p_3 \rangle $$
Component form: \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\)
Find component form from initial point, P to terminal point Q: \(\overset{\rightharpoonup}{v} = \langle q_1 - p_1, q_2 - p_2, q_3 - p_3 \rangle\)
Vector operations in three dimensions are essentially the same as in two dimension, just include z. See lesson 6-03 for indepth explanations.
Let \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\) and \(\overset{\rightharpoonup}{u} = \langle u_1, u_2, u_3 \rangle\).
Addition: Add corresponding elements.
$$ \overset{\rightharpoonup}{v} + \overset{\rightharpoonup}{u} = \langle v_1 + u_1, v_2 + u_2, v_3 + u_3 \rangle $$
Scalar Multiplication: Distribute the scalar to all the components.
$$ c\overset{\rightharpoonup}{v} = \langle cv_1, cv_2, cv_3 \rangle $$
Dot Product: Add products of corresponding elements.
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = v_1 u_1 + v_2 u_2 + v_3 u_3 $$
Magnitude: Distance between the initial and terminal points.
$$ \| \overset{\rightharpoonup}{v} \| = \sqrt{v_1^2 + v_2^2 + v_3^2} $$
Unit Vector: Divide vector by its magnitude to get a vector in direction of \(\overset{\rightharpoonup}{v}\) but length 1.
$$ \frac{\overset{\rightharpoonup}{v}}{\| \overset{\rightharpoonup}{v} \|} $$
The dot product can be used to find the angle between vectors. Dot product can be found by adding the products of corresponding components
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = v_1 u_1 + v_2 u_2 + v_3 u_3 $$
The dot product can also be found by multiplying the magnitudes of the vectors with the cosine of the angle between the vectors.
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = \| \overset{\rightharpoonup}{v} \| \| \overset{\rightharpoonup}{u} \| \cos θ $$
So, if the dot product and magnitudes are known, or can be calculated, then the angle between the vectors can be found. The angle will always be between 0 and π radians (0 and 180°). Because cosine is zero at \(\frac{π}{2}\), the dot product equals zero if the vectors are orthogonal (perpendicular).
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = \| \overset{\rightharpoonup}{v} \| \| \overset{\rightharpoonup}{u} \| \cos θ $$
If \(\overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = 0\), then the vectors are orthogonal, or perpendicular.
If \(\overset{\rightharpoonup}{v} = c\overset{\rightharpoonup}{u}\), then the vectors are parallel.
Let \(\overset{\rightharpoonup}{m} = ⟨1, 0, 3⟩\) and \(\overset{\rightharpoonup}{n} = ⟨−2, 1, −4⟩\). (a) Find \(\| \overset{\rightharpoonup}{m} \|\), (b) find the unit vector in the direction of \(\overset{\rightharpoonup}{m}\), and (c) find \(\overset{\rightharpoonup}{m} + 2\overset{\rightharpoonup}{n}\).
Solutions
Use the distance formula with the components to find the magnitude.
$$ \| \overset{\rightharpoonup}{m} \| = \sqrt{𝑚_1^2 + 𝑚_2^2 + 𝑚_3^2} $$
$$ \qquad = \sqrt{1^2 + 0^2 + 3^2} $$
$$ \qquad = \sqrt{10} $$
To find a unit vector, divide the vector by its magnitude. The magnitude was evaluated in part a.
$$ \frac{\overset{\rightharpoonup}{m}}{\| \overset{\rightharpoonup}{m} \|} = \frac{⟨1, 0, 3⟩}{\sqrt{10}} $$
$$ \qquad = \left\langle \frac{1}{\sqrt{10}}, \frac{0}{\sqrt{10}}, \frac{3}{\sqrt{10}} \right\rangle $$
$$ \qquad = \left\langle \frac{\sqrt{10}}{10}, 0, \frac{3\sqrt{10}}{10}\right\rangle $$
Fill in the component form for the vectors first.
$$ \overset{\rightharpoonup}{m} + 2\overset{\rightharpoonup}{n} $$
⟨1, 0, 3⟩ + 2 ⟨−2, 1, −4⟩
Follow the order of operations, so do the scalar multiplication by distributing the 2.
⟨1, 0, 3⟩ + ⟨−4, 2, −8⟩
Add the vectors by adding corresponding elements.
⟨−3, 2, −5⟩
Let \(\overset{\rightharpoonup}{a} = ⟨-2, 4, 1⟩\) and \(\overset{\rightharpoonup}{b} = ⟨−1, 2, 0⟩\). (a) Find \(\| \overset{\rightharpoonup}{b} \|\), (b) find the unit vector in the direction of \(\overset{\rightharpoonup}{b}\), and (c) find \(-2\overset{\rightharpoonup}{a} + \overset{\rightharpoonup}{b}\).
Answers
\(\sqrt{5}\); \(\left\langle -\frac{1}{5}, \frac{2}{5}, 0\right\rangle\)
Let \(\overset{\rightharpoonup}{m} = ⟨1, 0, 3⟩\) and \(\overset{\rightharpoonup}{n} = ⟨−2, 1, −4⟩\). (a) Find \(\overset{\rightharpoonup}{𝑚}⋅\overset{\rightharpoonup}{n}\) and (b) find the angle between \(\overset{\rightharpoonup}{m}\) and \(\overset{\rightharpoonup}{n}\)
Solution
Multiply the corresponding components and then add the products.
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = v_1 u_1 + v_2 u_2 + v_3 u_3 $$
⟨1, 0, 3⟩ ⋅ ⟨−2, 1, −4⟩
1(−2) + 0(1) + 3(−4)
–14
The dot product was found in part a. Use that with the other dot product formula to find the angle.
$$ \overset{\rightharpoonup}{m}⋅\overset{\rightharpoonup}{n} = \| \overset{\rightharpoonup}{m} \| \| \overset{\rightharpoonup}{n} \| \cos θ $$
$$ −14 = \sqrt{1^2+0^2+3^2} \sqrt{(−2)^2+1^2+(−4)^2} \cos θ $$
$$ −14 = \sqrt{10} \sqrt{21} \cos θ $$
$$ \frac{−14}{\sqrt{10} \sqrt{21}} = \cos θ $$
θ ≈ 165.0°
Let \(\overset{\rightharpoonup}{a} = ⟨-2, 4, 1⟩\) and \(\overset{\rightharpoonup}{b} = ⟨−1, 2, 0⟩\). (a) Find \(\overset{\rightharpoonup}{a}·\overset{\rightharpoonup}{b}\) and (b) find the angle between \(\overset{\rightharpoonup}{a}\) and \(\overset{\rightharpoonup}{b}\)
Answers
10; 12.6°
Are \(\overset{\rightharpoonup}{p} = ⟨1, 5, −2⟩\) and \(\overset{\rightharpoonup}{q} = \left\langle −\frac{1}{5}, −1, \frac{2}{5} \right\rangle\) parallel, orthogonal, or neither?
Solution
Check to see is they are orthogonal. Vectors are orthogonal if \(\overset{\rightharpoonup}{p} ⋅ \overset{\rightharpoonup}{q} = 0\)
$$ ⟨1, 5, −2⟩⋅ \left\langle −\frac{1}{5}, −1, \frac{2}{5} \right\rangle $$
$$ 1\left(−\frac{1}{5}\right) + 5(−1) + (−2)\left(\frac{2}{5}\right) $$
$$ −\frac{1}{5} − 5 − \frac{4}{5} = −6 $$
This is not 0, so the vectors are not orthogonal.
The vectors are parallel if \(\overset{\rightharpoonup}{p} = c \overset{\rightharpoonup}{q}\).
$$ ⟨1, 5, −2⟩ = c \left\langle −\frac{1}{5}, −1, \frac{2}{5} \right\rangle $$
Check the x-components.
$$ 1 = c\left(−\frac{1}{5}\right) $$
c = −5
Check the y-components.
5 = c(−1)
c = −5
Check the z-components.
$$ −2 = c\left(\frac{2}{5}\right) $$
c = −5
Notice that c is always the same, so they are parallel.
Are \(\overset{\rightharpoonup}{p} = ⟨1, 0, −2⟩\) and \(\overset{\rightharpoonup}{q} = \left\langle 2, 5, 1 \right\rangle\) parallel, orthogonal, or neither?
Answer
orthogonal
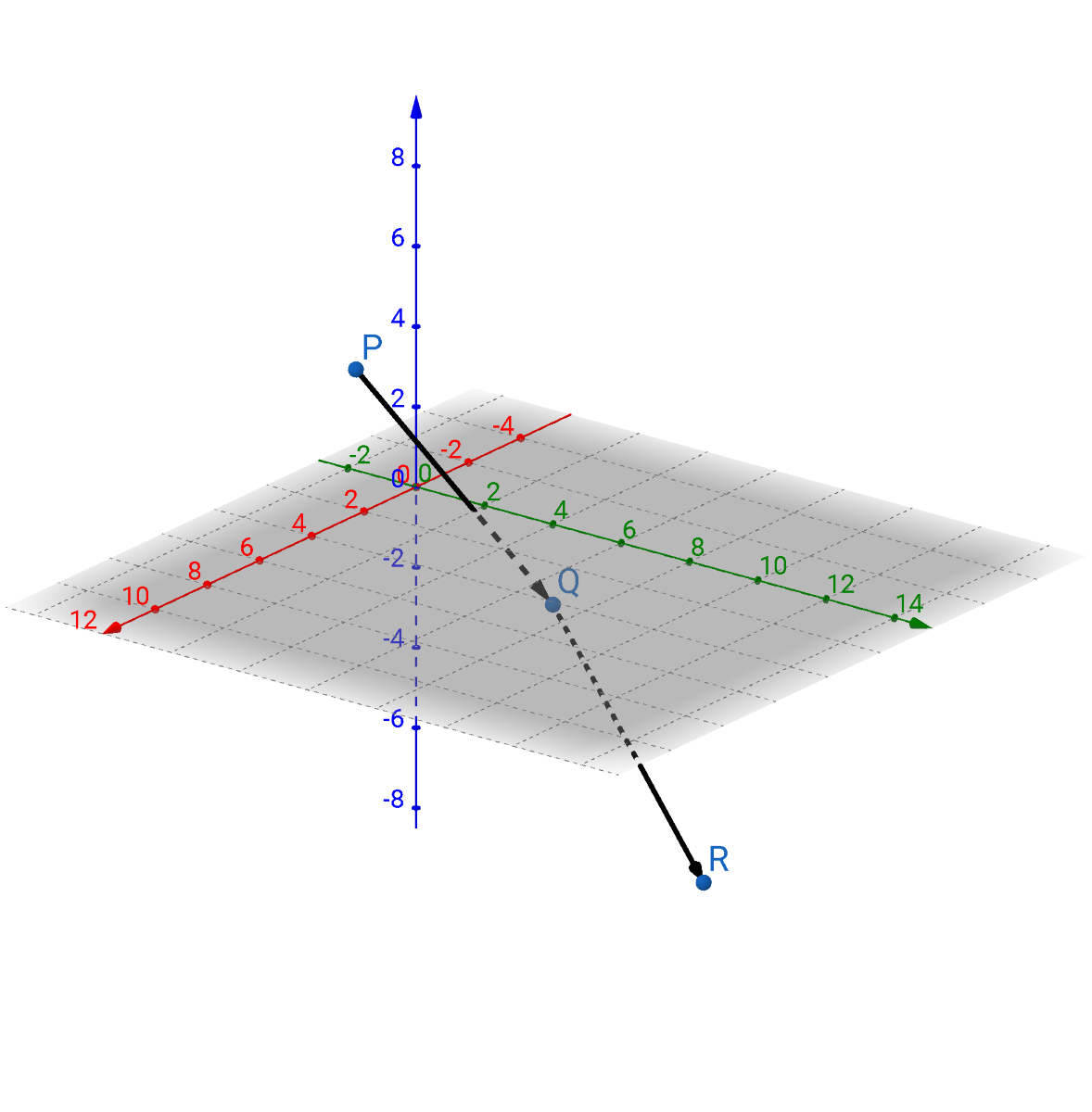
Are P(1, −1, 3), Q(0, 4, −2), and R(6, 13, −5) collinear?
Solution
If two vectors from the same point are parallel or antiparallel, then they would go in the same or opposite directions. Antiparallel means the vectors go in opposite directions. Either way, they would form a "line". So start by finding \(\overset{\rightharpoonup}{PQ}\) and \(\overset{\rightharpoonup}{QR}\) and see if they are parallel.
Find the vector by subtraction corresponding elements from the points. Terminal point - initial point.
$$ \overset{\rightharpoonup}{PQ} = ⟨0−1, 4−(−1), −2−3⟩ = ⟨−1, 5, −5⟩ $$
$$ \overset{\rightharpoonup}{QR} = ⟨6−0, 13−4, −5−(−2)⟩ = ⟨6, 9, −3⟩ $$
They would be parallel or antiparallel if \(\overset{\rightharpoonup}{PQ} = c \overset{\rightharpoonup}{QR}\).
⟨−1, 5, −5⟩ = c ⟨6, 9, −3⟩
Check the x-components.
−1 = c(6)
$$ -\frac{1}{6} = c $$
Check the y-components.
5 = c(9)
$$ \frac{5}{9} = c $$
The c is not the same, so the vectors are not parallel or antiparallel. So, they are not going same direction. Therefore, the vectors are not collinear.
Are A(2, −1, 4), B(1, 4, 3), and C(3, −15, 3) collinear?
Answer
Yes, they are collinear.
Component form: \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\)
Find component form from initial point, P to terminal point Q: \(\overset{\rightharpoonup}{v} = \langle q_1 - p_1, q_2 - p_2, q_3 - p_3 \rangle\)
Let \(\overset{\rightharpoonup}{v} = \langle v_1, v_2, v_3 \rangle\) and \(\overset{\rightharpoonup}{u} = \langle u_1, u_2, u_3 \rangle\).
Addition: Add corresponding elements.
$$ \overset{\rightharpoonup}{v} + \overset{\rightharpoonup}{u} = \langle v_1 + u_1, v_2 + u_2, v_3 + u_3 \rangle $$
Scalar Multiplication: Distribute the scalar to all the components.
$$ c\overset{\rightharpoonup}{v} = \langle cv_1, cv_2, cv_3 \rangle $$
Dot Product: Add products of corresponding elements.
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = v_1 u_1 + v_2 u_2 + v_3 u_3 $$
Magnitude: Distance between the initial and terminal points.
$$ \| \overset{\rightharpoonup}{v} \| = \sqrt{v_1^2 + v_2^2 + v_3^2} $$
Unit Vector: Divide vector by its magnitude to get a vector in direction of \(\overset{\rightharpoonup}{v}\) but length 1.
$$ \frac{\overset{\rightharpoonup}{v}}{\| \overset{\rightharpoonup}{v} \|} $$
$$ \overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = \| \overset{\rightharpoonup}{v} \| \| \overset{\rightharpoonup}{u} \| \cos θ $$
If \(\overset{\rightharpoonup}{v} \cdot \overset{\rightharpoonup}{u} = 0\), then the vectors are orthogonal, or perpendicular.
If \(\overset{\rightharpoonup}{v} = c\overset{\rightharpoonup}{u}\), then the vectors are parallel.
Helpful videos about this lesson.