Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
No one can serve two masters. Either you will hate the one and love the other, or you will be devoted to the one and despise the other. You cannot serve both God and money. Matthew 6:24 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.4.2
The speed limit sign like the one above are common to see along roads. The sign gives the maximum speed that you can legally drive on that road. You can legally approach that speed, but you cannot go over that speed. Mathematical limits are a similar concept.
In calculus, a limit is the value that a function approaches as you get arbitrarily near a x-value. Unlike a speed limit, you do not necessarily reach the value of the limit, but you get close enough to it to know what that value will be. It would be like driving your car 54.999999 mph. You are not at the limit of 55 mph, but you are close enough.
The formal definition of a limit is if f(x) becomes arbitrarily close to a unique number L as x approaches c from either side, then the limit of f(x) as x approaches c is L. It is written as
$$ \lim_{x \rightarrow c} f(x) = L $$
This is read "The limit as x approaches c of f(x) is L." It means that as x gets very close to c from both sides, then f(x) gets very close to L. Thus, the limit is L.
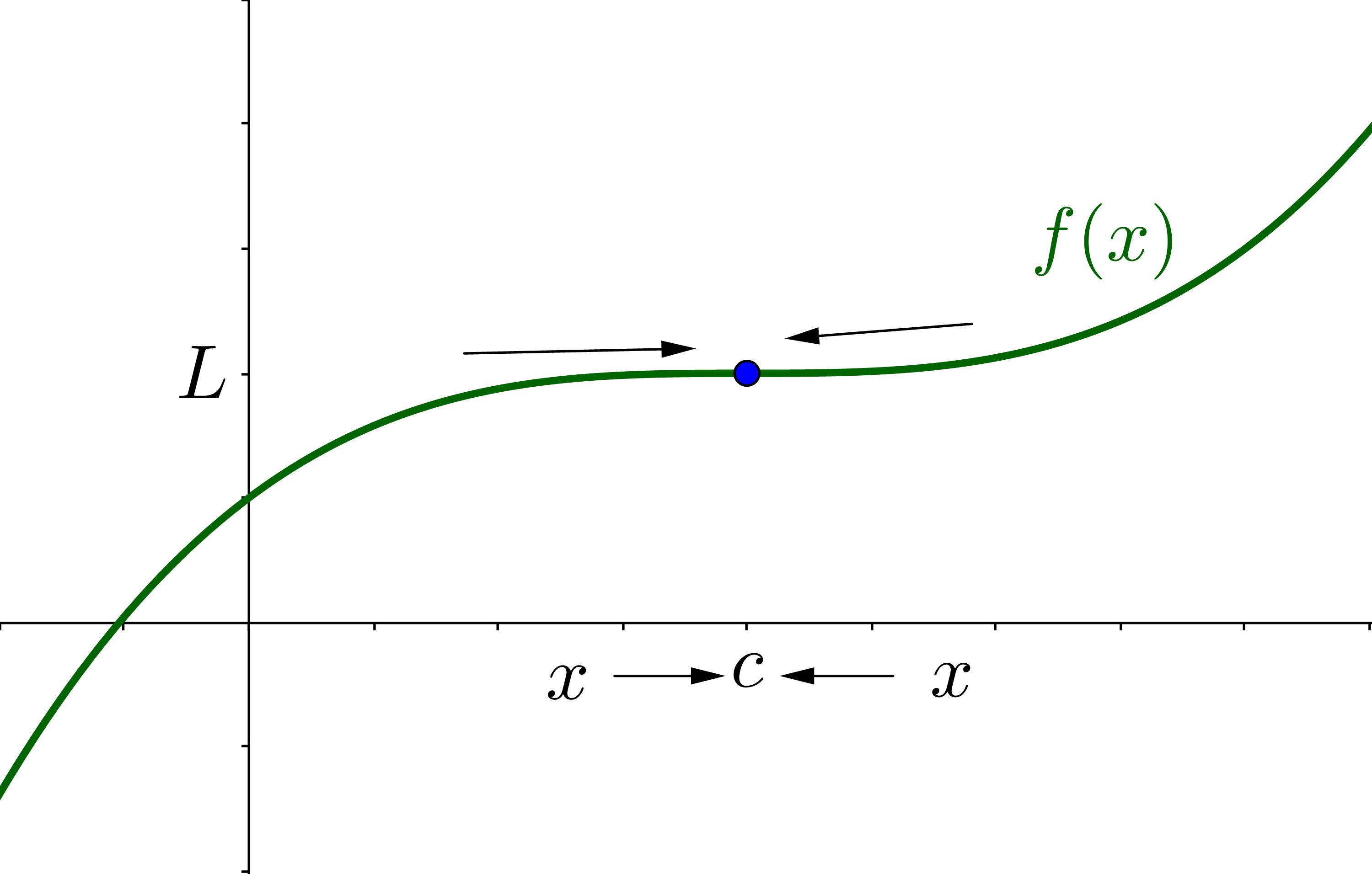
if f(x) becomes arbitrarily close to a unique number L as x approaches c from either side, then the limit of f(x) as x approaches c is L.
$$ \lim_{x \rightarrow c} f(x) = L $$
One way to calculate a limit is to make a table. Unlike the usual table that is often used in math, the x values are going to get closer to c by decimal places. For example, if you want the limit at 2, use the x-values such as 1.9, 1.99, 1.999, 1.9999, 2.0001, 2.001, 2.01, 2.1. This will let you see a pattern as you approach 2.
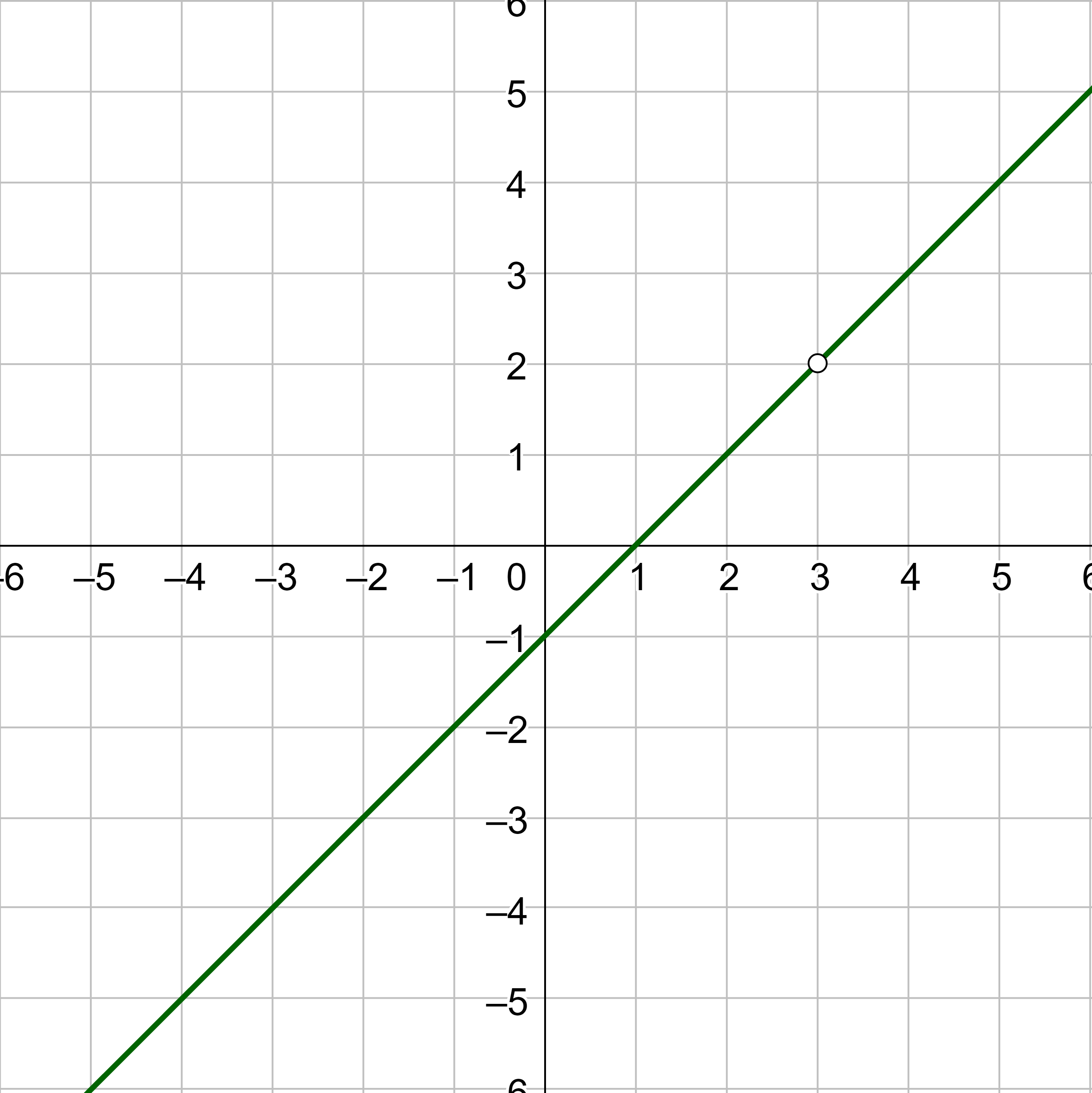
Use a table to evaluate \(\displaystyle \lim_{x \rightarrow 3} \frac{x^2 - 4x + 3}{x - 3}\)
Solution
The limit is near x = 3, so make a table near 3.
| x | 2.9 | 2.99 | 2.999 | 2.9999 | 3 | 3.0001 | 3.001 | 3.01 | 3.1 |
|---|---|---|---|---|---|---|---|---|---|
| f(x) | 1.9 | 1.99 | 1.999 | 1.9999 | __?__ | 2.0001 | 2.001 | 2.01 | 2.1 |
It appears from the pattern that the limit approaches 2. This can also be seen in the graph below. If there was not a hole in the graph, it would go through the point (3, 2).
$$ \lim_{x \rightarrow 3} \frac{x^2 - 4x + 3}{x - 3} = 2 $$
Use a table to evaluate \(\displaystyle \lim_{x \rightarrow 0} \frac{2x^3 - 3x}{x}\)
Answer
–3
The graph of the function does not necessarily need to go through a point for the limit to exist. The function in Example 1 has a hole in it and is undefined when x = 3, but the graph does approach 2 as x approaches 3. However, there are some limits that do not exist. There are three cases: (1) the function approaches different numbers from either side, (2) the function increases or decreases without bound, or (3) the function oscillates between two fixed values.
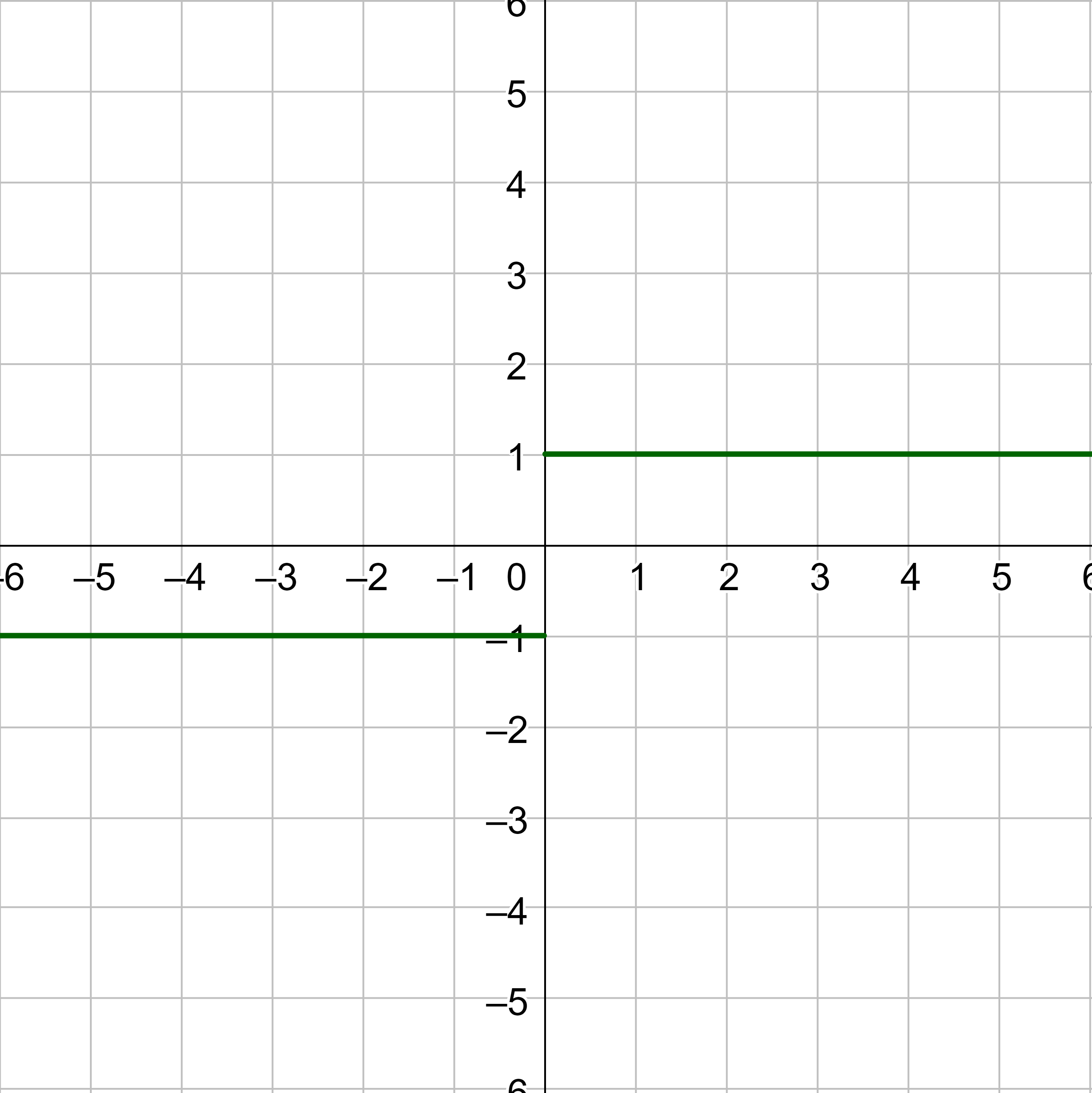
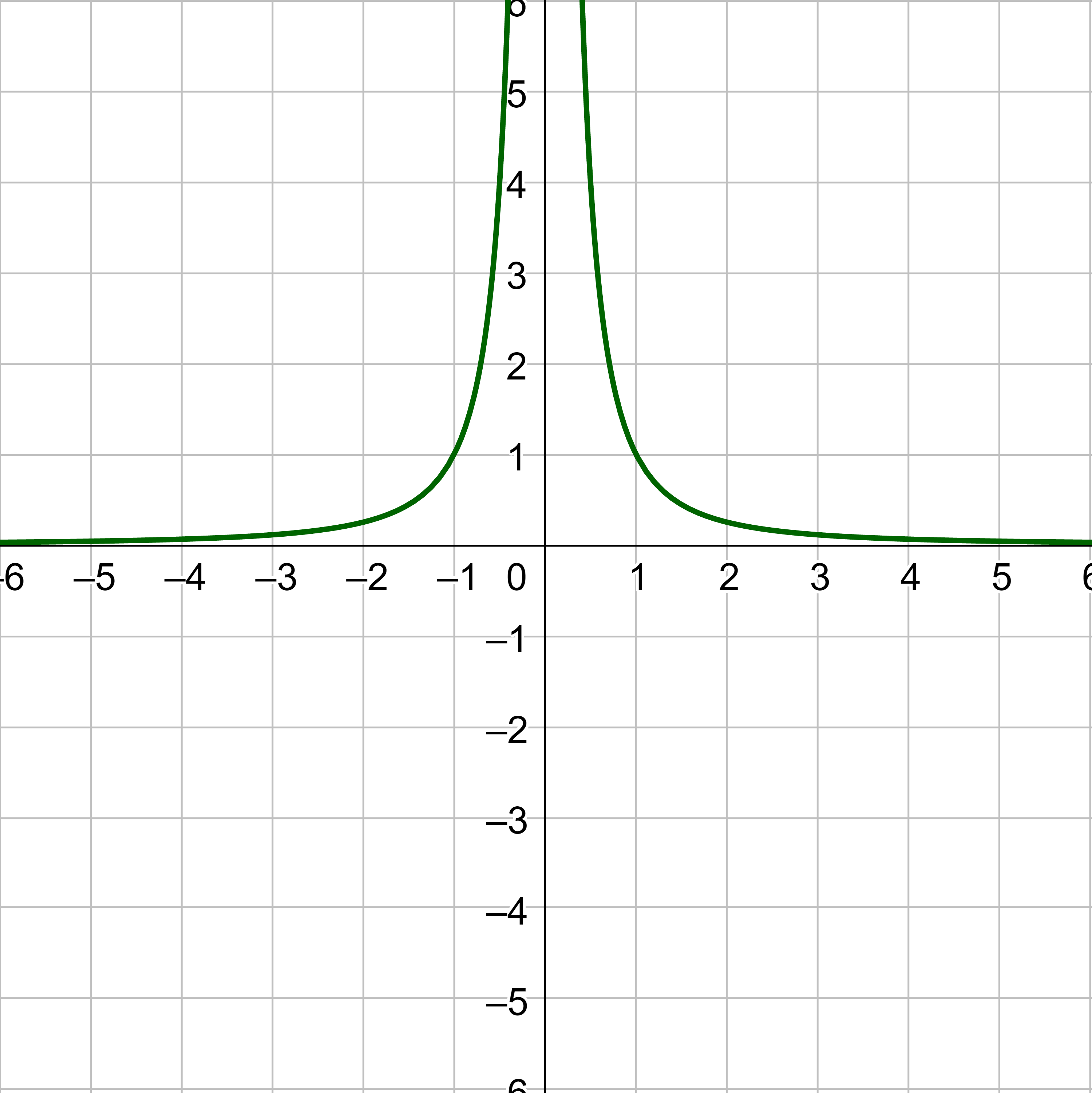
State whether the limit exists. If it does not, explain why not.
Solution
Make a quick graph on your calculator and look at the value x approaches.
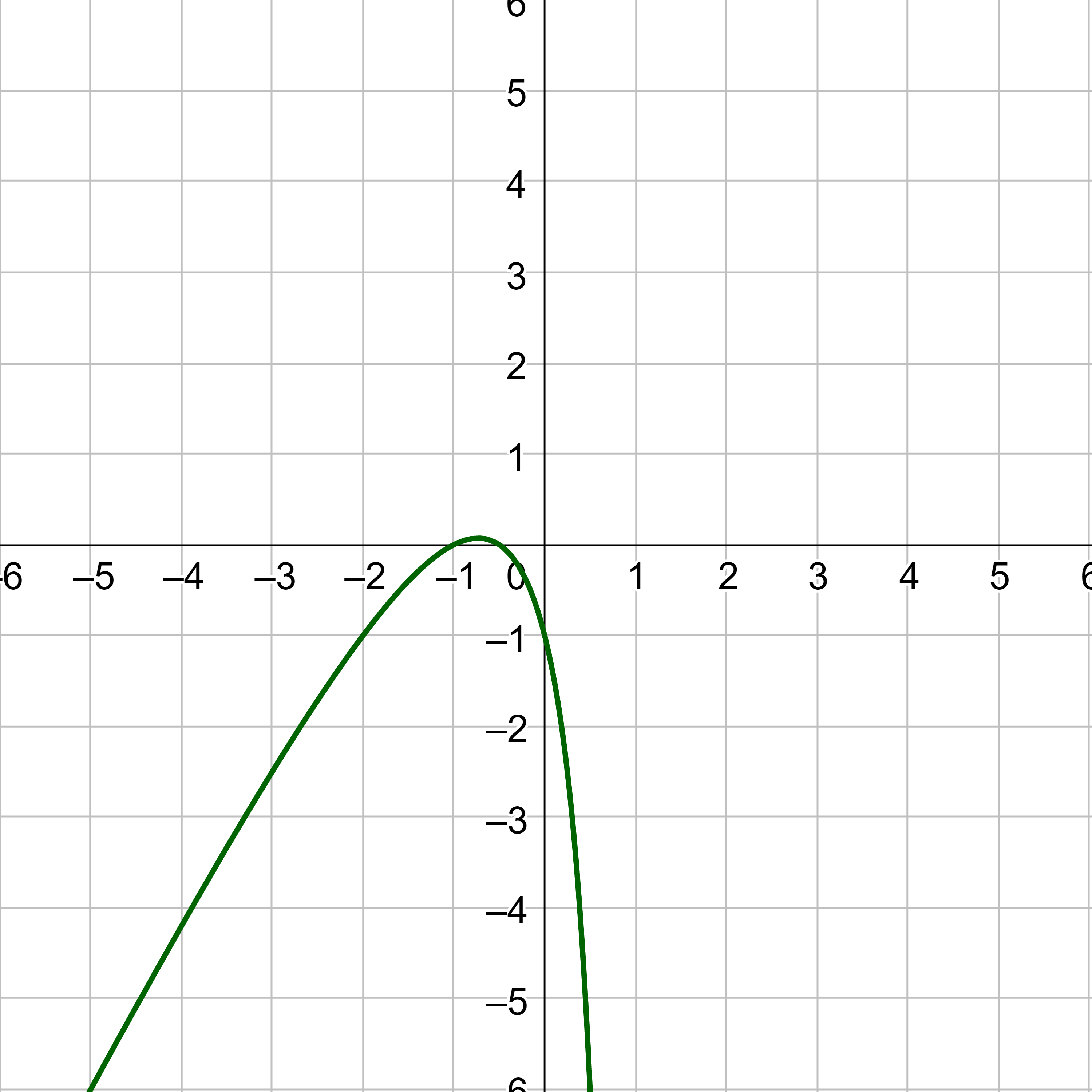
At x = 1, the graph goes both down towards –∞ from the left and up towards +∞ from the right. The limit does not exist because the function increases or decreases without bound.
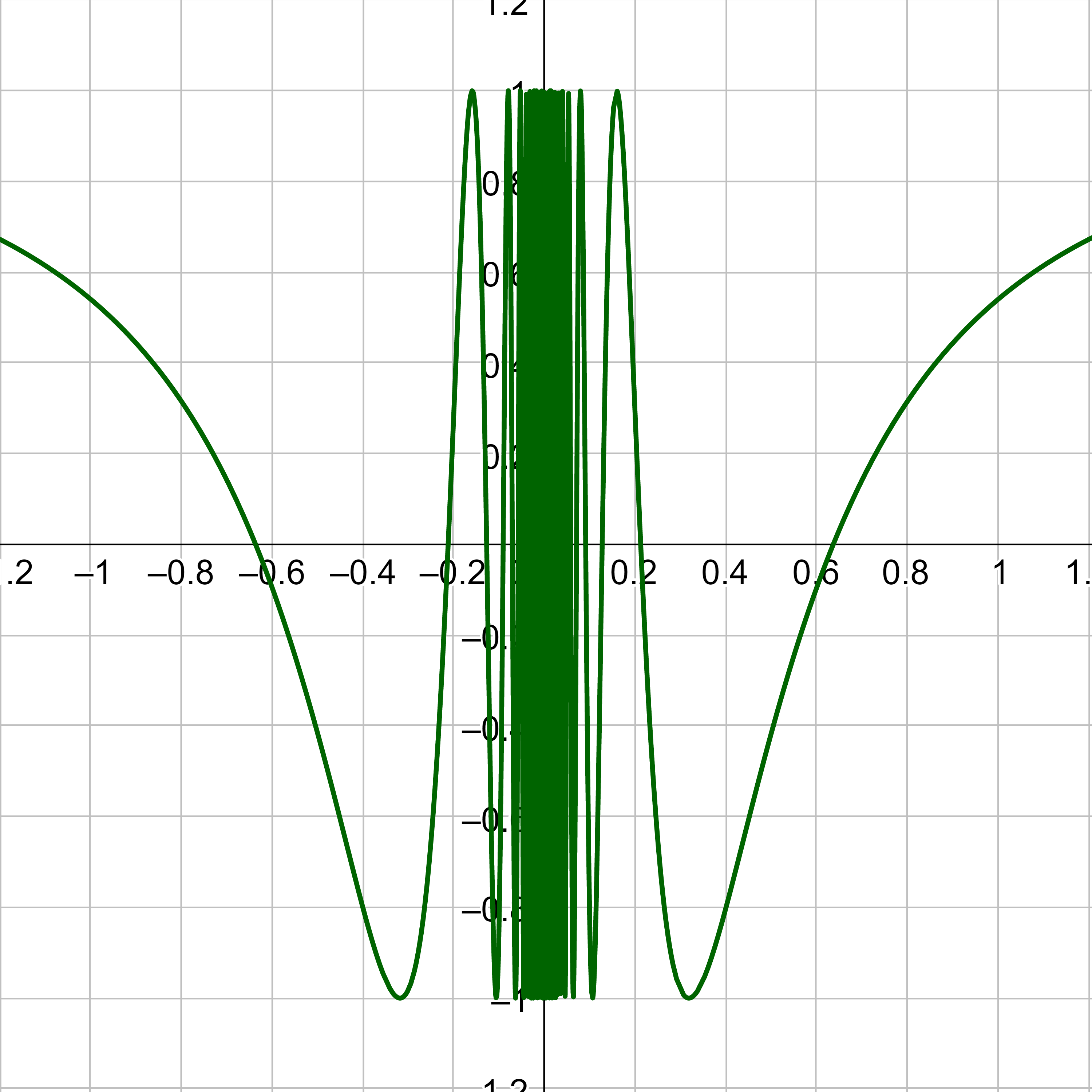
At x = 0, the graph oscillates between –1 and 1. Zoom in several times to see what happens. The limit does not exist because the function oscillates between two values.
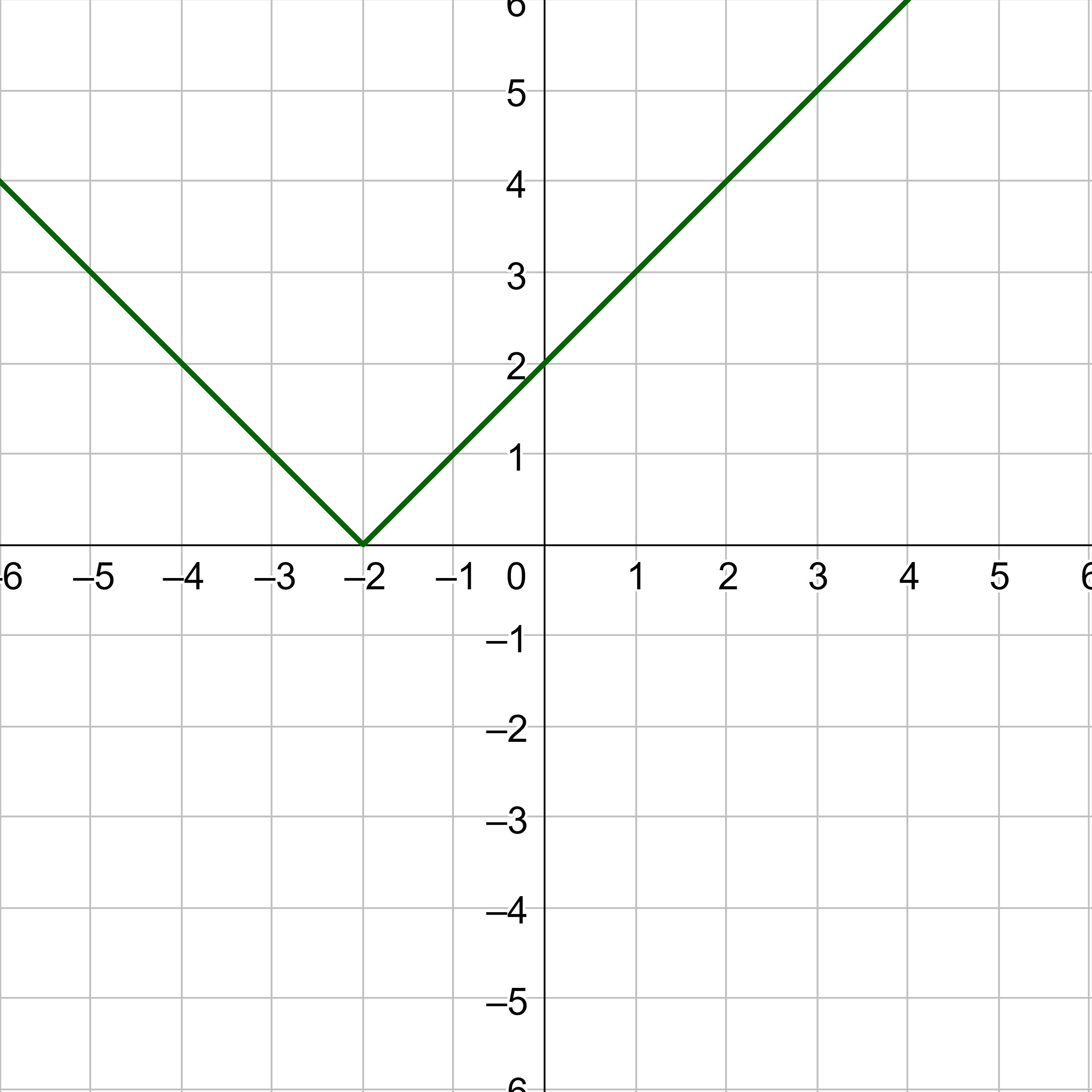
At x = –2, the graph approaches 0 from both sides, so the limit is 0.
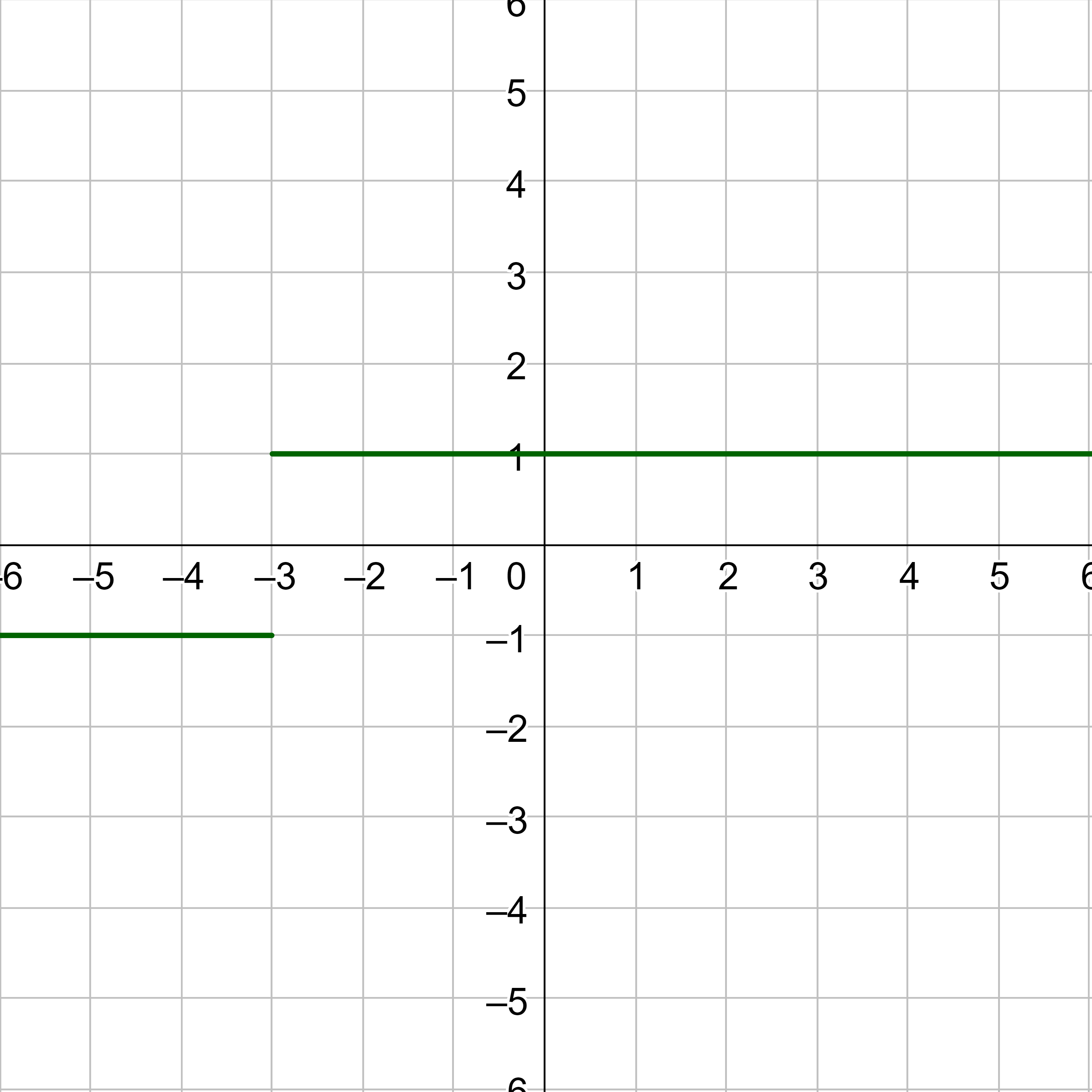
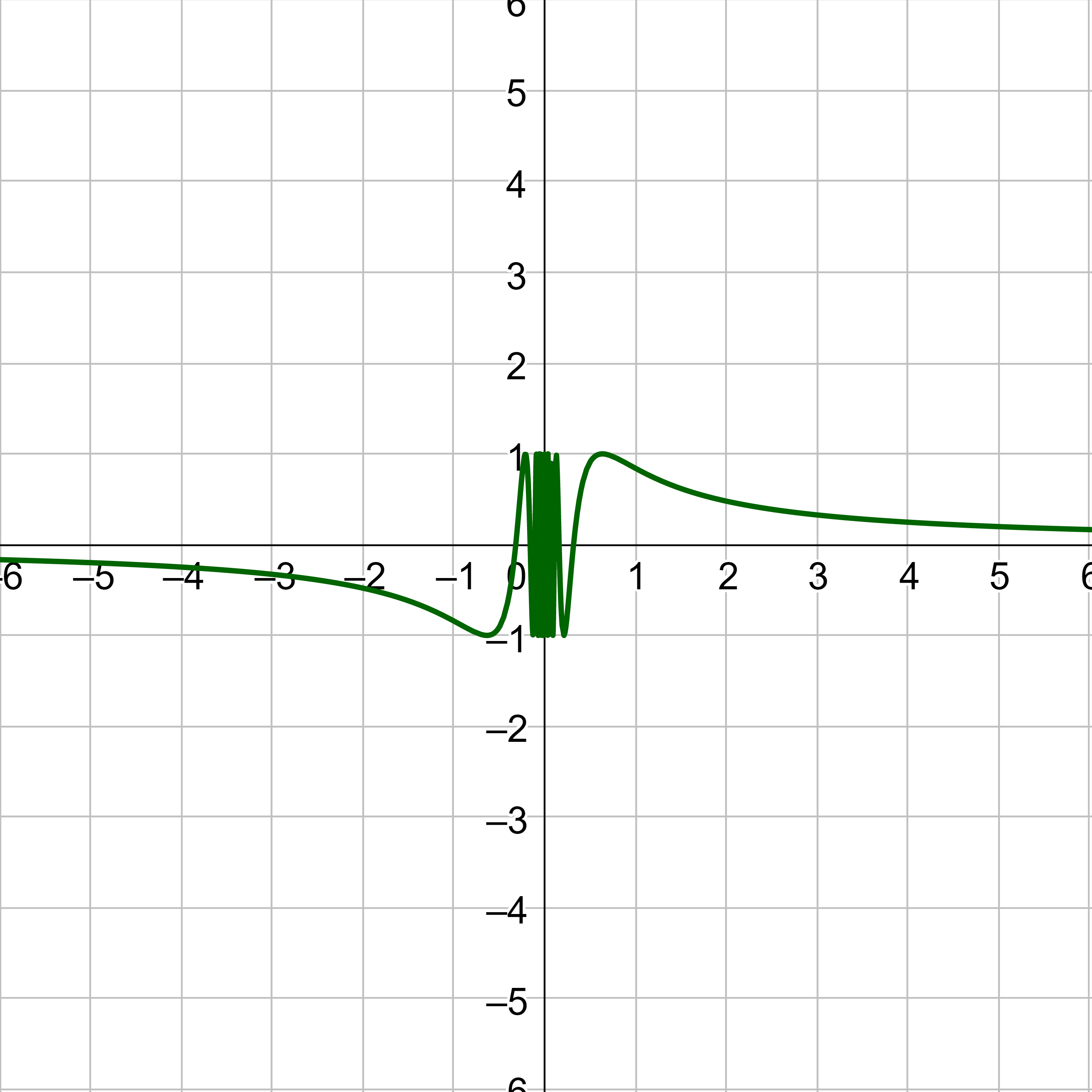
At x = –3, the graph approaches –1 from the left and 1 from the right. The limit does not exist because the function approaches different values from either side.
State whether the limit exists. If it does not, explain why not. \(\displaystyle \lim_{x \rightarrow 0} \frac{2}{x^2}\)
Answer
Does not exist because it increases without bound at x = 0.
Many limits can be evaluated simply by plugging in the value x approaches into the function. This is called direct substitution. The first few properties in the following list illustrate this. The other properties show how to combine limits.
Let \(\displaystyle \lim_{x \rightarrow c} f(x) = L\) and \(\displaystyle \lim_{x \rightarrow c} g(x) = K\).
Evaluate \(\displaystyle \lim_{x \rightarrow 2} 4x^3\)
Solution
The properties can be summarized as try to plug in the value x approaches. So in this case, plug in a 2.
$$ \lim_{x \rightarrow 2} 4x^3 $$
= 4(2)3
= 32
Evaluate \(\displaystyle \lim_{x \rightarrow -1} (2x^2 - 3x + 5)\).
Solution
x approaches −1, so try plugging it in.
$$ \lim_{x \rightarrow -1} (2x^2 - 3x + 5) $$
= 2(−1)2 − 3(−1) + 5
= 10
Evaluate \(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x + 1}}{2x}\).
Solution
x approaches 0, so try plugging in a 0.
$$ \lim_{x \rightarrow 0} \frac{\sqrt{x + 1}}{2x} $$
$$ = \frac{\sqrt{0 + 1}}{2(0)} $$
$$ = \frac{1}{0} $$
Since you cannot divide by 0, this limit Does not exist.
Evaluate \(\displaystyle \lim_{x \rightarrow 1} \frac{x^2 - 2x}{x}\)
Answer
–1 (This exists because the function is defined at x = 1. \(\displaystyle \lim_{x \rightarrow 0} \frac{x^2 - 2x}{x}\) does not exist because it increases without bound at x = 0.)
if f(x) becomes arbitrarily close to a unique number L as x approaches c from either side, then the limit of f(x) as x approaches c is L.
$$ \lim_{x \rightarrow c} f(x) = L $$
Let \(\displaystyle \lim_{x \rightarrow c} f(x) = L\) and \(\displaystyle \lim_{x \rightarrow c} g(x) = K\).
Helpful videos about this lesson.