Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


I have set you an example that you should do as I have done for you. John 13:15 NIV

12-02 Evaluate Limits

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.4.2

0/0
(wikimedia: Jonas Ericsson)

The last lesson showed how to evaluate limits by direct substitution. It also showed how to evaluate limits using tables or graphs, including limits that could not use direct substitution such as limits at holes in graphs. But, what if direct substitution gives \(\frac{0}{0}\)? \(\frac{0}{0}\) is undefined and could be 0, 1, or anything else. We could use a table, but it would be nice if there was an algebraic method to calculate the limit.

The Indeterminant Form

A limit that gives \(\frac{0}{0}\) is in the indeterminant form. An indeterminant limit must calculated using various techniques.

Indeterminant Form

$$ \lim_{x \rightarrow c} f(x) = \frac{0}{0} $$

Techniques for Evaluating

Dividing Out Technique

Lesson 12-01 showed how to use a table to evaluate a limit at a hole in the graph. The dividing out technique can be used to evaluate limits of rational functions at a hole. The steps are (1) factor the numerator and denominator, (2) cancel factors, and (3) evaluate the limit using direct substitution.

Dividing Out Technique

Evaluate \(\displaystyle \lim_{x \rightarrow -5} \frac{x^2 + 2x - 15}{x + 5}\)

Solution

Start by trying direct substitution.

$$ \lim_{x \rightarrow -5} \frac{x^2 + 2x - 15}{x + 5} $$

$$ = \frac{(-5)^2 + 2(-5) - 15}{-5 + 5} = \frac{0}{0} $$

Since the limit is indeterminant, try the dividing out technique. Start by factoring.

$$ \lim_{x \rightarrow -5} \frac{(x + 5)(x - 3)}{(x + 5)} $$

Now cancel the factor, in this case (x + 5).

$$ \lim_{x \rightarrow -5} (x - 3) $$

= (−5) − 3

= −8

graph of problem
\(\displaystyle \lim_{x \rightarrow -5} \frac{x^2 + 2x - 15}{x + 5} = -8\)

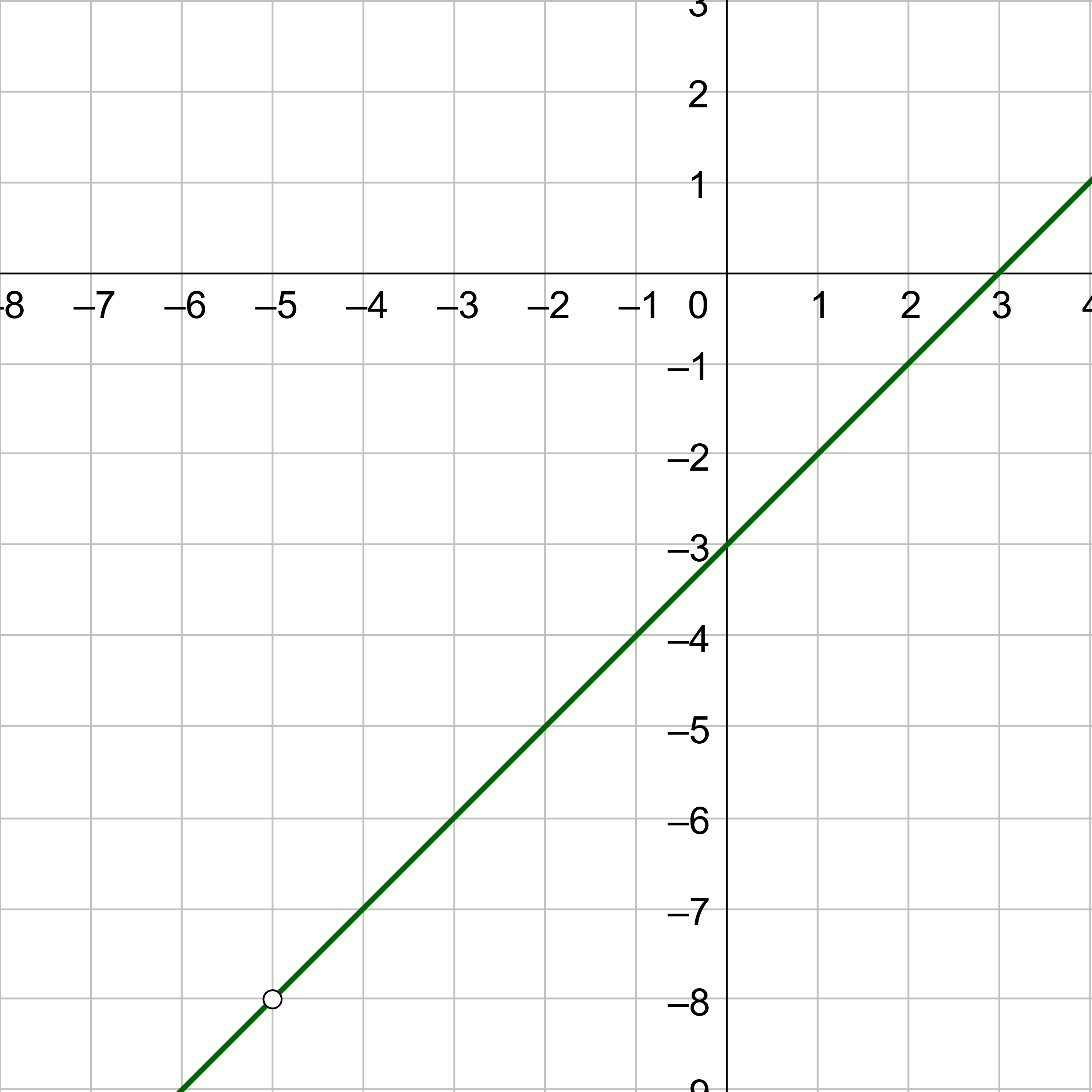
Evaluate \(\displaystyle \lim_{x \rightarrow 0} \frac{-2x^2 + x}{x}\)

Answer

1

Rationalizing Technique

Usually, rationalizing is used to remove any radicals from the denominator of a fraction. This is done by multiplying the numerator and denominator by the conjugate of the denominator. However, in the case of indeterminant limits that contain radicals, multiply by the conjugate of the numerator to remove the radical from there. This often allows the evaluation of the limit using direct substitution. The steps for the rationalizing technique are (1) multiply the numerator and denominator by the conjugate of the numerator and (2) evaluate the limit by direct substitution.

Rationalizing Technique

Evaluate \(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x+4}−2}{x}\).

Solution

Start by trying direct substitution.

$$ \lim_{x \rightarrow 0} \frac{\sqrt{x+4}−2}{x} $$

$$ = \frac{\sqrt{0+4}-2}{0} = \frac{0}{0} $$

Because there is a square root, try the rationalizing technique. Start by multiplying the numerator and denominator by the conjugate of the numerator.

$$ \lim_{x \rightarrow 0} \frac{\left(\sqrt{x+4}−2\right)}{x} \frac{\left(\sqrt{x+4}+2\right)}{\left(\sqrt{x+4}+2\right)} $$

$$ \lim_{x \rightarrow 0} \frac{(x+4)−4}{x\left(\sqrt{x+4}+2\right)} $$

$$ \lim_{x \rightarrow 0} \frac{x}{x\left(\sqrt{x+4}+2\right)} $$

The x cancels.

$$ \lim_{x \rightarrow 0} \frac{1}{\sqrt{x+4}+2} $$

Now evaluate the limit with direct substitution.

$$ = \frac{1}{\sqrt{0+4}+2} $$

$$ = \frac{1}{4} $$

graph of problem
\(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x+4}−2}{x} = \frac{1}{4}\)

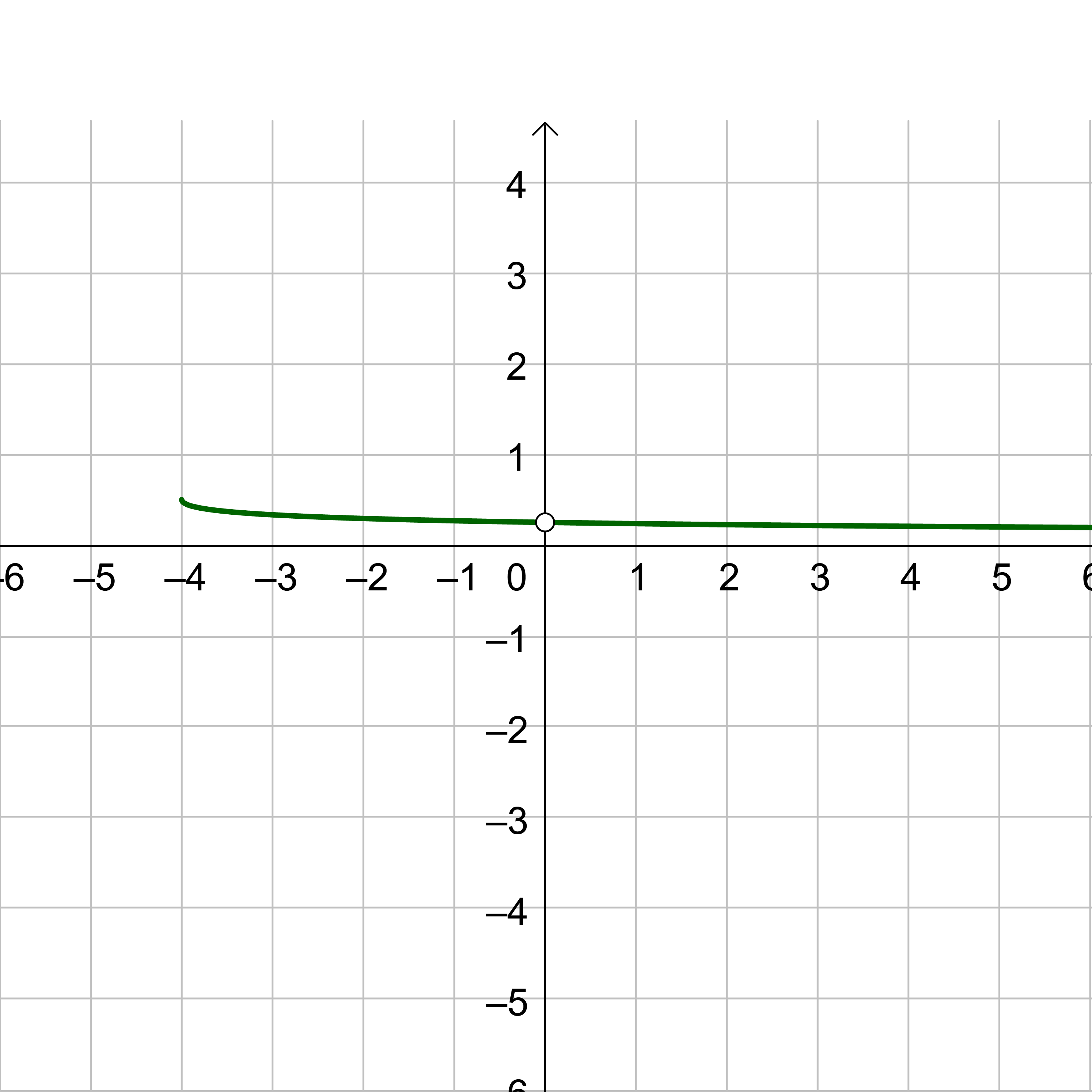
Evaluate \(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x+16}−4}{x}\)

Answer

\(\frac{1}{8}\)

One-Sided Limits

Sometimes a graph stops such as at 0 on \(f(x) = \sqrt{x}\), or there is a discontinuity where the graph approaches two different values from either side such as at 0 on \(g(x) = \frac{|x|}{x}\). These limits can only be calculated from one side.

One-Sided Limits

A one-sided limit is a limit found from only one direction.

\(\displaystyle \lim_{x \rightarrow c^{-}} f(x)\) means approach from the left.

\(\displaystyle \lim_{x \rightarrow c^{+}} f(x)\) means approach from the right.

One-Sided Limit

Evaluate (a) \(\displaystyle \lim_{x \rightarrow -1^-} \frac{4|x+1|}{x+1}\), and (b) \(\displaystyle \lim_{x \rightarrow -1^+} \frac{4|x+1|}{x+1}\).

Solution

  1. Try direct substitution.

    $$ \lim_{x \rightarrow -1^-} \frac{4|x+1|}{x+1} $$

    $$ = \frac{4|-1+1|}{-1+1} = \frac{0}{0} $$

    Neither the Dividing Out Technique nor the Rationalizing Technique apply here because it is not a polynomial nor a radical. So a graph or table is used.

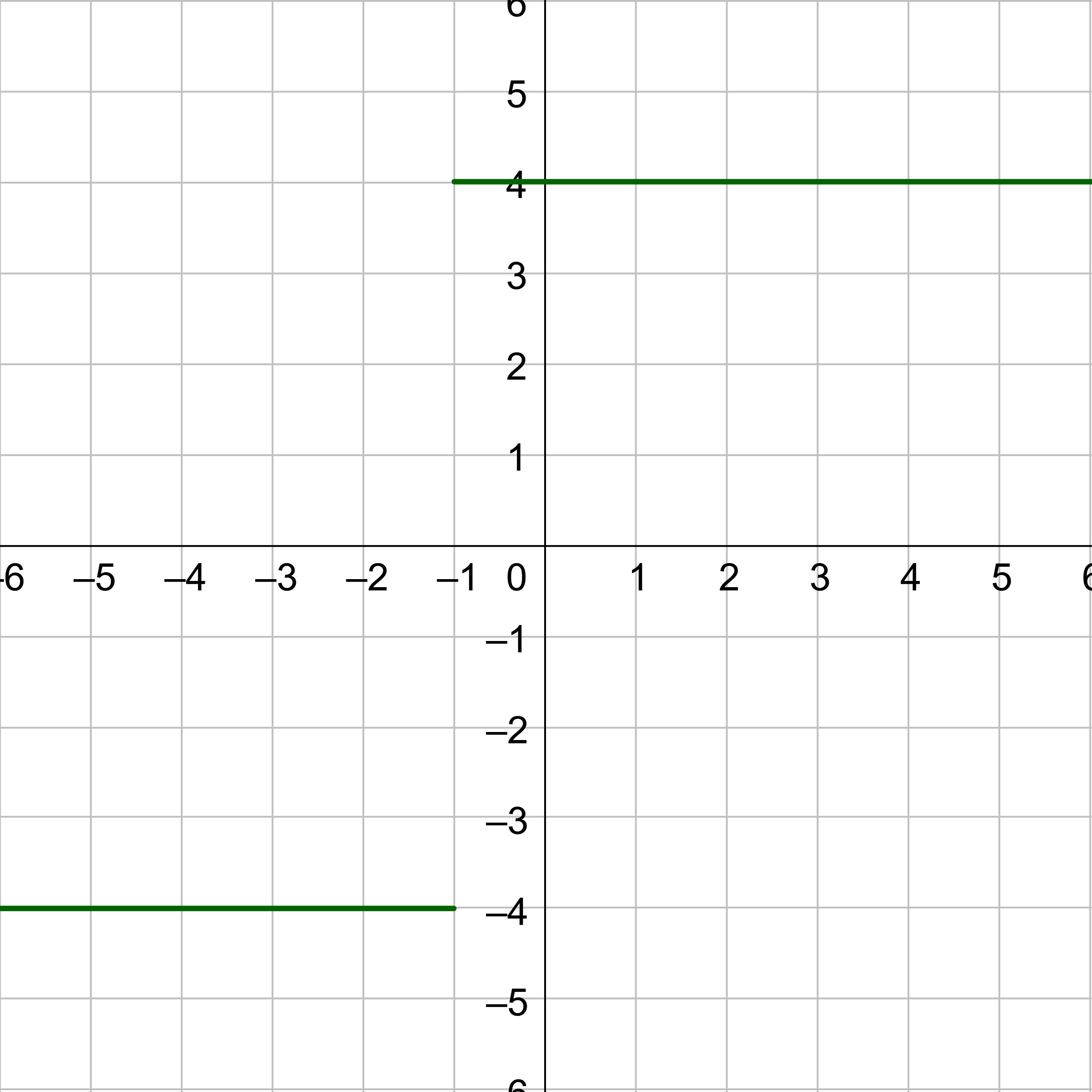
    graph of problem
    \(f(x) = \frac{4|x+1|}{x+1}\)

    Follow the graph from the left towards x = −1. The graph is constant at y = −4. So the \(\displaystyle \lim_{x \rightarrow -1^-} \frac{4|x+1|}{x+1} = -4\).

  2. The limit is the same function, but from the right this time. Look at the graph in figure 4. This time follow the graph from the right side towards x = −1. The graph is constant at y = 4. So the \(\displaystyle \lim_{x \rightarrow -1^+} \frac{4|x+1|}{x+1} = 4\).

Evaluate (a) \(\displaystyle \lim_{x \rightarrow 0^-} \left\{\begin{align} x + 4, &x ≤ 0 \\ x^3, &x > 0 \end{align}\right.\), and (b) \(\displaystyle \lim_{x \rightarrow 0^+} \left\{\begin{align} x + 4, &x ≤ 0 \\ x^3, &x > 0 \end{align}\right.\).

Answer

4; 0

A Limit from Calculus

This chapter is an introduction to calculus. In fact, there have been little introductions to calculus all through the book. Lesson 1-04 introduced the difference quotient \(\frac{f(x + h) - f(x)}{h}\). Now put a limit on it.

$$ \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$

This limit always gives the indeterminant \(\frac{0}{0}\) and needs the special techniques to evaluate it.

Limit from Calculus

For the function f(x) = 3x2 + 4 evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}\).

Solution

Start by filling the function f(x) = 3x2 + 4 into the limit.

$$ \lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h} $$

$$ \lim_{h \rightarrow 0} \frac{(3(1+h)^2 + 4) - (3(1)^2 + 4)}{h} $$

Simplify

$$ \lim_{h \rightarrow 0} \frac{(3(1+2h+h^2)+4)-(7)}{h} $$

$$ \lim_{h \rightarrow 0} \frac{3 + 6h + 3h^2 + 4 - 7}{h} $$

$$ \lim_{h \rightarrow 0} \frac{6h + 3h^2}{h} $$

Direct substitution will produce the indeterminant case, so use the dividing out technique.

$$ \lim_{h \rightarrow 0} \frac{h(6 + 3h)}{h} $$

$$ \lim_{h \rightarrow 0} (6 + 3h) $$

Now use direct substitution.

= 6 + 3(0)

= 6

For the function f(x) = x3 evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(-1+h)-f(-1)}{h}\).

Answer

3

Lesson Summary
Indeterminant Form

$$ \lim_{x \rightarrow c} f(x) = \frac{0}{0} $$

Techniques for Evaluating
One-Sided Limits

A one-sided limit is a limit found from only one direction.

\(\displaystyle \lim_{x \rightarrow c^{-}} f(x)\) means approach from the left.

\(\displaystyle \lim_{x \rightarrow c^{+}} f(x)\) means approach from the right.

Helpful videos about this lesson.

Practice Exercises

  1. Evaluate the limit.
  2. \(\displaystyle \lim_{x \rightarrow 2} \frac{x^2 + 3x - 10}{x - 2}\)
  3. \(\displaystyle \lim_{x \rightarrow 3} \frac{x^2 - 7x + 12}{x^2 - 3x}\)
  4. \(\displaystyle \lim_{x \rightarrow -1} \frac{x^3 + 4x^2 + 3x}{x + 1}\)
  5. \(\displaystyle \lim_{x \rightarrow 2} \frac{x - 2}{x^2 - 12x + 20}\)
  6. \(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x + 9} - 3}{x}\)
  7. \(\displaystyle \lim_{x \rightarrow 0} \frac{\sqrt{x + 25} - 5}{x}\)
  8. \(\displaystyle \lim_{x \rightarrow 1} \frac{\sqrt{x + 3} - 2}{x - 1}\)
    1. \(\displaystyle \lim_{x \rightarrow 0^{+}} \frac{5x}{| x |}\)
    2. \(\displaystyle \lim_{x \rightarrow 0^{- }} \frac{5x}{| x |}\)
    1. \(\displaystyle \lim_{x \rightarrow 1^{+}} \left\{\begin{align} 2x + 3, &x < 1 \\ -x^2 + 1, &x ≥ 1 \end{align} \right.\)
    2. \(\displaystyle \lim_{x \rightarrow 1^{-}} \left\{\begin{align} 2x + 3, &x < 1 \\ -x^2 + 1, &x ≥ 1 \end{align} \right.\)
    1. \(\displaystyle \lim_{x \rightarrow -2^{+}} \left\{\begin{align} \sqrt{x + 3}, &x ≤ -2 \\ x, &x > -2 \end{align} \right.\)
    2. \(\displaystyle \lim_{x \rightarrow -2^{-}} \left\{\begin{align} \sqrt{x + 3}, &x ≤ -2 \\ x, &x > -2 \end{align} \right.\)
  12. Evaluate the limit from calculus.
  13. For the function f(x) = 2x2 evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(2+h)-f(2)}{h}\).
  14. For the function f(x) = x2 + 3 evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}\).
  15. For the function f(x) = x2 − 2x evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(-1+h)-f(-1)}{h}\).
  16. For the function f(x) = 2x3 + x evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(-2+h)-f(-2)}{h}\).
  17. For the function \(f(x) = \frac{1}{x}\) evaluate \(\displaystyle \lim_{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}\).
  18. Mixed Review
  19. (12-01) Evaluate \(\displaystyle \lim_{x \rightarrow 3} (2x^3 - 18x)\).
  20. (12-01) Evaluate \(\displaystyle \lim_{x \rightarrow -2} \frac{x^2 - 9}{x + 2}\).
  21. (11-04) Find the distance from (2, 0, 1) to 2x + y + 3z − 2 = 0.
  22. (10-02) Evaluate the sum: \(\displaystyle \sum_{i = 1}^{15} (i^2 + 3i)\)
  23. (10-02) Evaluate the sum: \(\displaystyle \sum_{r = 1}^{20} \left(\frac{4}{3} πr^3\right)\)

Answers

  1. 7
  2. \(-\frac{1}{3}\)
  3. –2
  4. \(-\frac{1}{8}\)
  5. \(\frac{1}{6}\)
  6. \(\frac{1}{10}\)
  7. \(\frac{1}{4}\)
  8. 5; −5
  9. 0; 5
  10. −2; 1
  11. 8
  12. 2
  13. −4
  14. 25
  15. −1
  16. 0
  17. Does not exist
  18. \(\frac{5\sqrt{14}}{14}\)
  19. 1600
  20. 58800π