Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Jesus replied: “‘Love the Lord your God with all your heart and with all your soul and with all your mind.’ This is the first and greatest commandment. And the second is like it: ‘Love your neighbor as yourself.’” Matthew 22:37-39 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.4.2, PC.6.4
Velocity is the rate-of-change of position. That means it is how quickly position is changing. Acceleration is the rate-of-change of velocity. In other words, acceleration is how quickly velocity is changing.
Calculus mainly focuses on two problems. The first problem is finding the rate-of-change of functions. This is called finding a derivative. Graphically this is represented by finding the slope of the line tangent to a function. Remember that slopes are rates-of-change. The second problem is finding the area under a curve on a graph. This is called a integral. Integrals also happen to be the opposite of derivatives.
This lesson is about derivatives and rates-of-change. To derive the formula for rate-of-change, start with the slope formula for two points whose x-values are separated by h: (x, f(x)) and (x + h, f(x + h)). See figure 2.
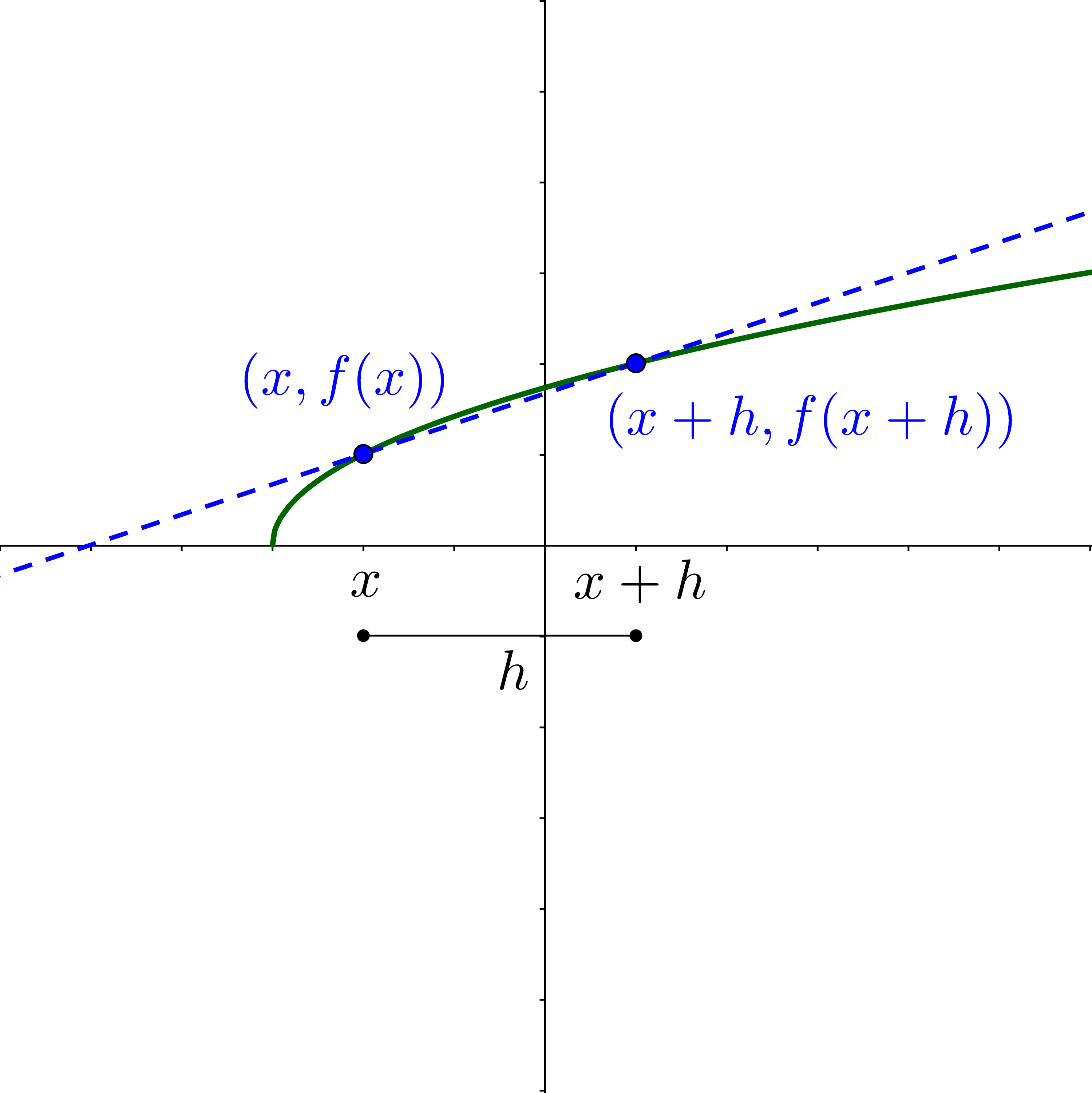
$$ Slope = m = \frac{y_2 - y_1}{x_2 - x_1} $$
$$ Slope = \frac{f(x + h) - f(x)}{x + h - x} $$
$$ Slope = \frac{f(x + h) - f(x)}{h} $$
This gives us the average rate-of-change between two points, but if the instantaneous, or exact, slope at a given point is wanted, h must be zero. So, take the limit as h approaches 0. This produces a function that is called a derivative and is denoted by f′(x). To find the rate-of-change, plug in the x-value of the location of the desired slope.
$$ Slope = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$
The rate-of-change at a location is found by plugging in the x-value of the location.
Find the derivative of f(x) = x2 + 3
Solution
Find f(x + h).
f(x + h) = (x + h)2 + 3
Substitute f(x + h) and f(x) into the derivative formula.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{\color{blue}{f(x + h)} - \color{red}{f(x)}}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(\color{blue}{(x + h)^2 + 3}) - (\color{red}{x^2 + 3})}{h} $$
Simplify the numerator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(x^2 + 2xh + h^2 + 3) - (x^2 + 3)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{2xh + h^2}{h} $$
Factor the h out of the numerator and then cancel the h from the numerator and denominator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{h(2x + h)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} (2x + h) $$
Now evaluate the limit by plugging in 0 for h.
f ′(x) = 2x + 0
f ′(x) = 2x
Find the derivative of f(x) = x2 − 2x.
Solution
Find f(x + h).
f(x + h) = (x + h)2 − 2(x + h)
Substitute f(x + h) and f(x) into the derivative formula.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{\color{blue}{f(x + h)} - \color{red}{f(x)}}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(\color{blue}{(x + h)^2 - 2(x + h)}) - (\color{red}{x^2 - 2x})}{h} $$
Simplify the numerator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(x^2 + 2xh + h^2 - 2x - 2h) - (x^2 - 2x)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{2xh + h^2 - 2h}{h} $$
Factor the h out of the numerator and then cancel the h from the numerator and denominator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{h(2x + h - 2)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} (2x + h - 2) $$
Now evaluate the limit by plugging in 0 for h.
f ′(x) = 2x + 0 − 2
f ′(x) = 2x − 2
Find the derivative of f(x) = 2x³.
Answer
f ′(x) = 6x2
Find the derivative of \(f(x) = \sqrt{x} - 2\).
Solution
Find f(x + h).
$$ f(x + h) = \sqrt{x + h} - 2 $$
Substitute f(x + h) and f(x) into the derivative formula.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{\color{blue}{f(x + h)} - \color{red}{f(x)}}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(\color{blue}{\sqrt{x + h} - 2}) - (\color{red}{\sqrt{x} - 2})}{h} $$
Simplify the numerator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{\sqrt{x + h} - \sqrt{x}}{h} $$
Use the rationalizing technique.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(\sqrt{x + h} - \sqrt{x})}{h} \frac{(\sqrt{x + h} + \sqrt{x})}{(\sqrt{x + h} + \sqrt{x})} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(x + h) - (x)}{h(\sqrt{x + h} + \sqrt{x})} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{h}{h(\sqrt{x + h} + \sqrt{x})} $$
Cancel the h from the numerator and denominator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{1}{\sqrt{x + h} + \sqrt{x}} $$
Now evaluate the limit by plugging in 0 for h.
$$ f′(x) = \frac{1}{\sqrt{x + 0} + \sqrt{x}} $$
$$ f′(x) = \frac{1}{\sqrt{x} + \sqrt{x}} $$
$$ f′(x) = \frac{1}{2\sqrt{x}} $$
Find the derivative of \(f(x) = \sqrt{x + 1}\).
Answer
\(f′(x) = \frac{1}{2\sqrt{x + 1}}\)
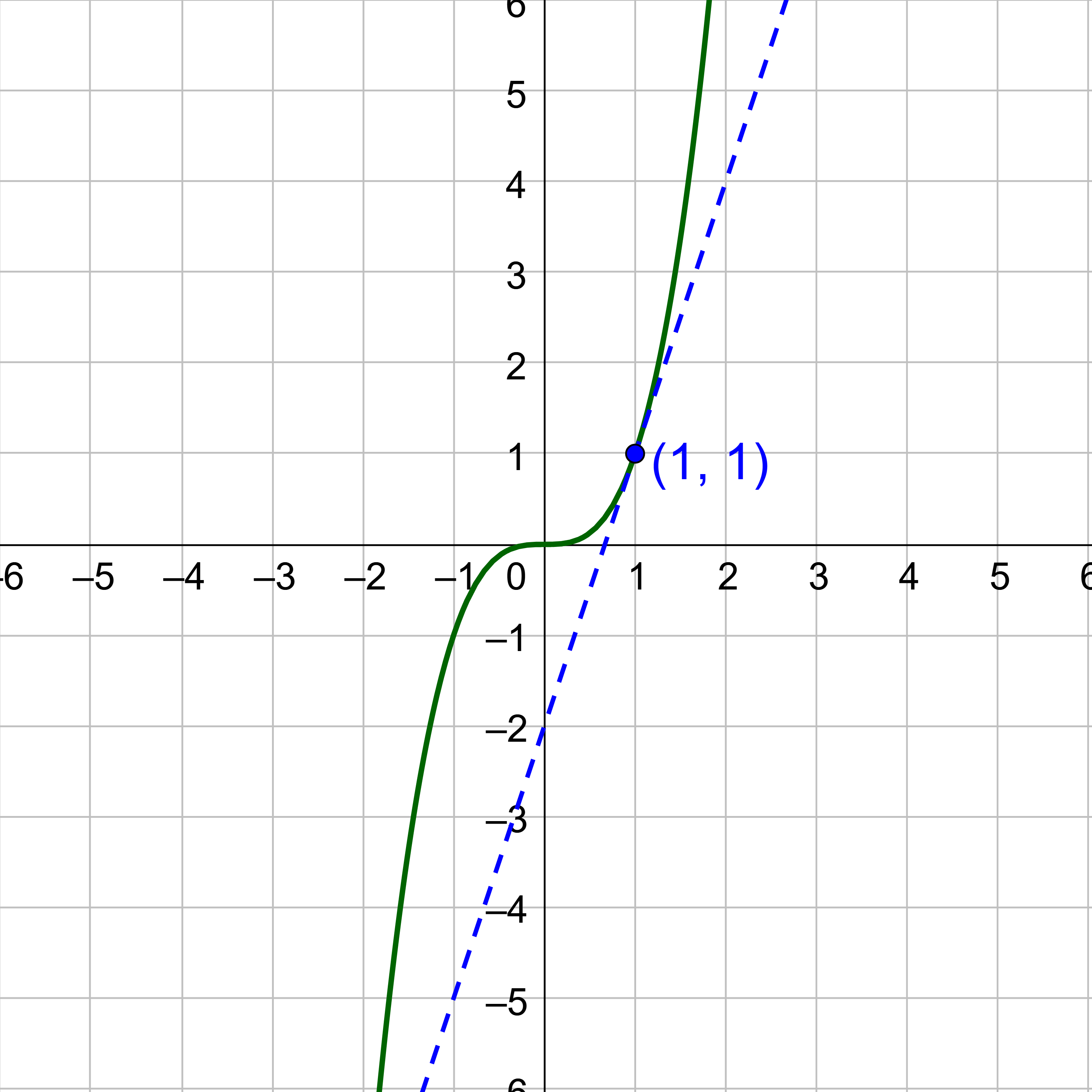
Find the slope of f(x) = x3 at (1, 1).
Solution
Start by finding the derivative. So, find f(x + h).
f(x + h) = (x + h)3
Substitute f(x + h) and f(x) into the derivative formula.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{\color{blue}{f(x + h)} - \color{red}{f(x)}}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(\color{blue}{(x + h)^3}) - (\color{red}{x^3})}{h} $$
Simplify the numerator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{(x^3 + 3x^2h + 3xh^2 + h^3) - (x^3)}{h} $$
Factor the h out of the numerator and then cancel the h from the numerator and denominator.
$$ f′(x) = \lim_{h \rightarrow 0} \frac{3x^2h + 3xh^2 + h^3}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} \frac{h(3x^2 + 3xh + h^2)}{h} $$
$$ f′(x) = \lim_{h \rightarrow 0} 3x^2 + 3xh + h^2 $$
Now evaluate the limit by plugging in 0 for h.
f ′(x) = 3x2 + 3x(0) + (0)2
f ′(x) = 3x2
Find the slope at (1, 1) by plugging in x = 1.
f ′(2) = 3(1)2 = 3
The slope of the tangent line at (1, 1) is 3.
Find the slope of f(x) = 2x2 − 4 at (–1, –2).
Answer
–4
$$ f′(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} $$
The rate-of-change at a location is found by plugging in the x-value of the location.
Helpful videos about this lesson.