Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Then Jesus said to his disciples, “Whoever wants to be my disciple must deny themselves and take up their cross and follow me. For whoever wants to save their life will lose it, but whoever loses their life for me will find it.” Matthew 16:24-25 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.4.2
Derivatives, or rates-of-change, are the first major part of calculus. Finding integrals, or areas, are the second major part. Calculating an integral involves adding together an infinite number of tiny areas. For example, the surface area of the soccer ball can be estimated by adding up the area of the colored polygons. A better estimate could be found by adding up the areas of the smaller leather polygons that are stitched together. An even better estimate would be to split the area into an infinite number of infinitely tiny areas, and add those areas together. This is done by taking the limit of a function as x approaches infinity. That limit is the focus of this lesson.
A limit at infinity can be found by using the fact that \(f(x) = \frac{1}{x}\) has a horizontal asymptote at y = 0. That means that as x approaches infinity, the function approaches zero. The same is true if f(x) has any exponent. Some limits at infinity can then be evaluating by splitting them into several simplified fractions where xn is the denominator of each fraction.
$$ \lim_{x \rightarrow ∞} \frac{1}{x^n} = 0 $$
$$ \lim_{x \rightarrow -∞} \frac{1}{x^n} = 0 $$
Evaluate \(\displaystyle \lim_{x \rightarrow ∞} \frac{1 - 3x + 2x^2}{x^2}\).
Solution
Start by splitting the function into separate fractions with the same denominator.
$$ \lim_{x \rightarrow ∞} \frac{1 - 3x + 2x^2}{x^2} $$
$$ \lim_{x \rightarrow ∞} \left(\frac{1}{x^2} - \frac{3x}{x^2} + \frac{2x^2}{x^2}\right) $$
Simplify each fraction.
$$ \lim_{x \rightarrow ∞} \left(\frac{1}{x^2} - \frac{3}{x} + 2\right) $$
Evaluate the limit of each term.
= 0 − 0 + 2
= 2
Evaluate \(\displaystyle \lim_{x \rightarrow ∞} \frac{5x^3 - 2x^2 + 3x - 14}{x^3}\).
Answer
5
The limit at infinity is the same as the value of the horizontal asymptote for the function. Thus, the same shortcuts for finding horizontal asymptotes also work to find limits at infinity.
If f(x) is a rational function, then \(\displaystyle \lim_{x \rightarrow ∞} f(x)\) is found by
Let N = degree of the numerator
Let D = degree of the denominator
Evaluate
Solution
Start by finding the degree of the numerator (N) and the degree of the denominator (D).
$$ \lim_{x \rightarrow ∞} \frac{x^{\color{blue}{1}} - 3}{2x^{\color{red}{2}} + 4x + 5} $$
N = 1; D = 2
N < D, so \(\displaystyle \lim_{x \rightarrow ∞} \frac{x - 3}{2x^2 + 4x + 5} = 0\).
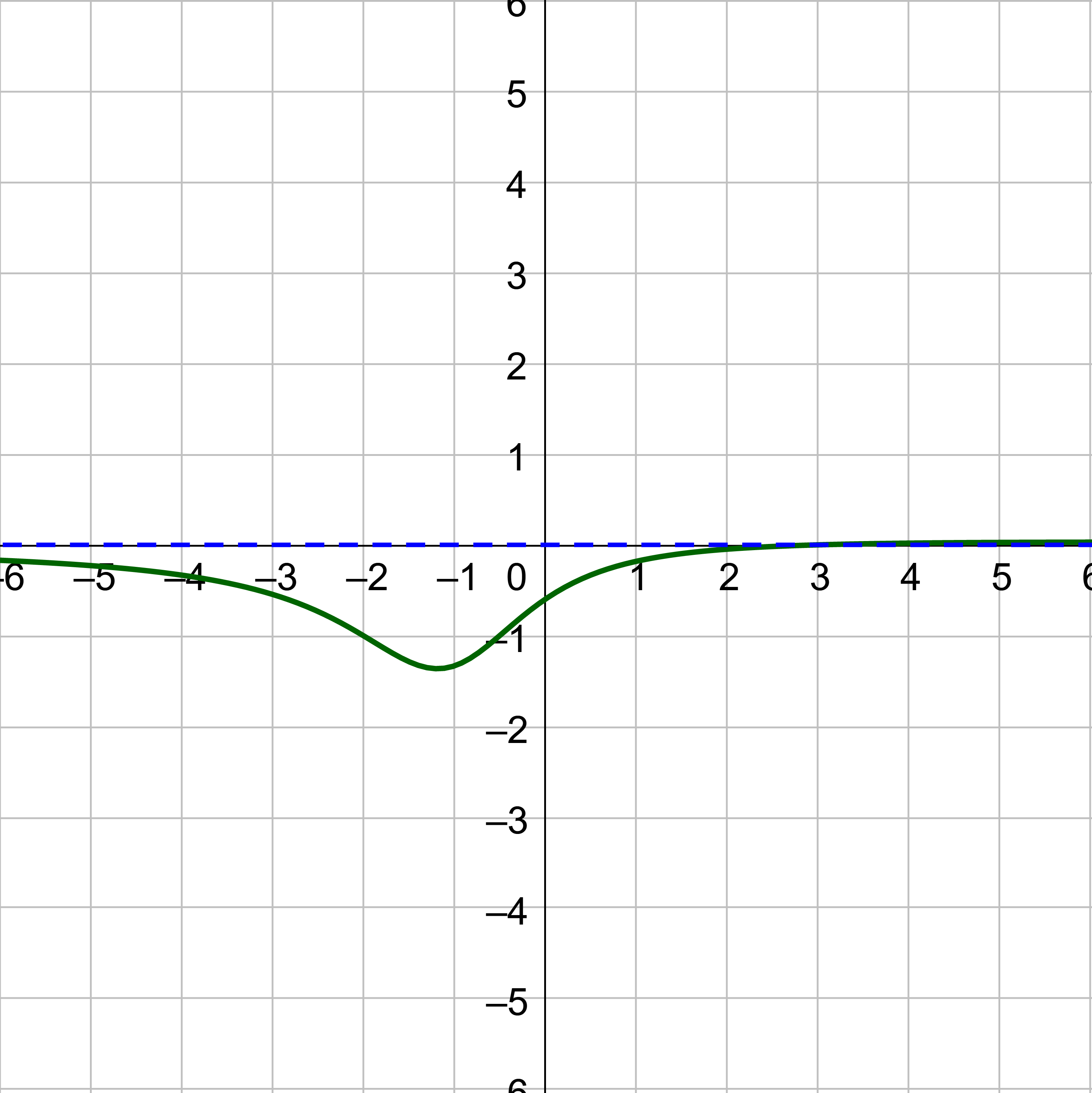
Start by finding the degree of the numerator (N) and the degree of the denominator (D).
$$ \lim_{x \rightarrow ∞} \frac{x^2 - 3}{2x^2 + 4x + 5} $$
N = 2; D = 2
N = D, so the limit is the leading coefficients. \(\displaystyle \lim_{x \rightarrow ∞} \frac{x^2 - 3}{2x^2 + 4x + 5} = \frac{1}{2}\).
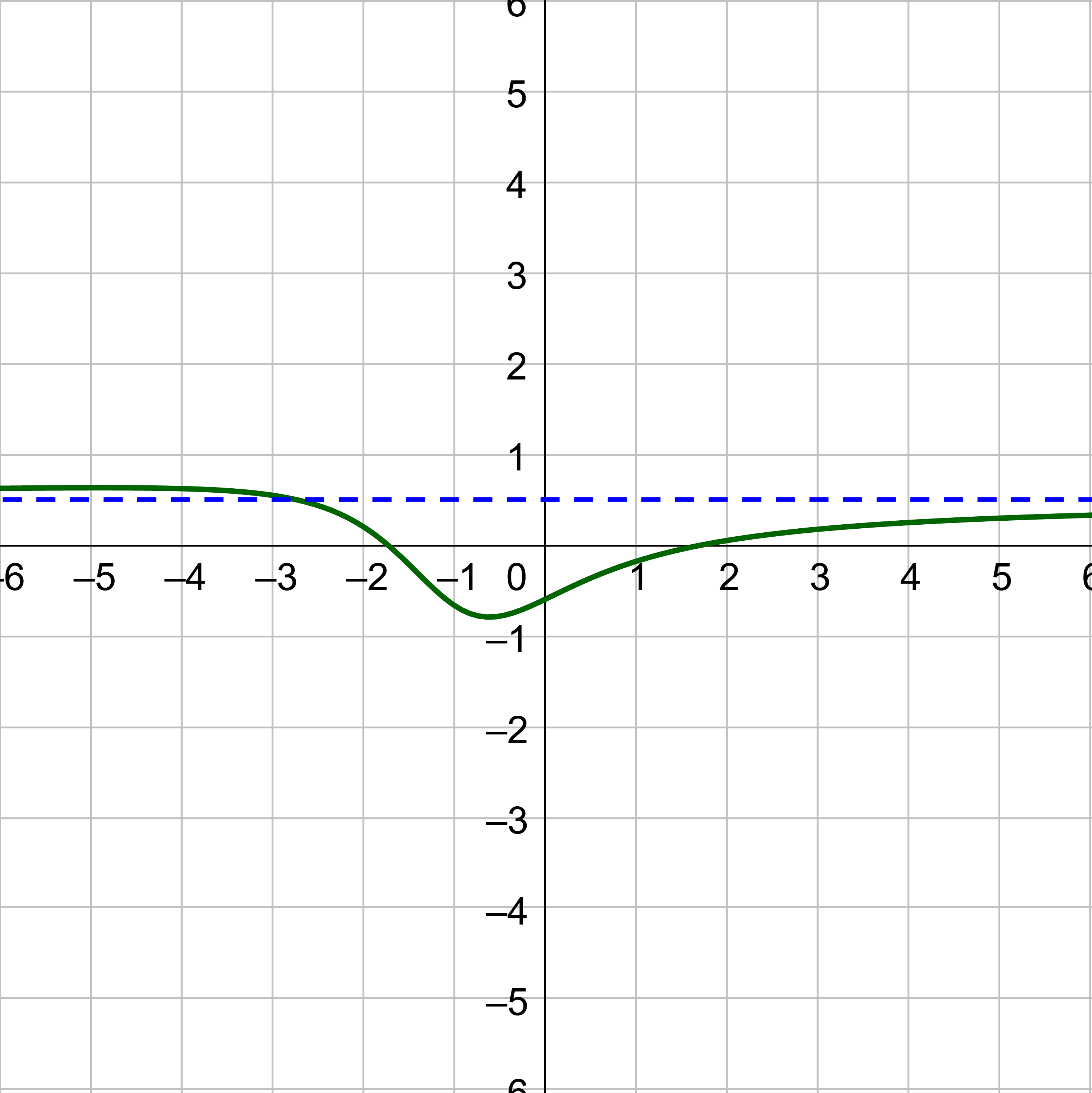
Start by finding the degree of the numerator (N) and the degree of the denominator (D).
$$ \lim_{x \rightarrow ∞} \frac{x^3 - 3}{2x^2 + 4x + 5} $$
N = 3; D = 2
N > D, so the limit does not exist. \(\displaystyle \lim_{x \rightarrow ∞} \frac{x^3 - 3}{2x^2 + 4x + 5}\) does not exist.
Evaluate \(\displaystyle \lim_{x \rightarrow ∞} \frac{3x^4 + 2x^3 - 5x + 10}{2x^4 + 16}\)
Answer
\(\frac{3}{2}\)
The limit of a sequence is the value the terms tend to approach. If the sequences terms approach a single number, then the sequence converges. If the sequence terms do not approach a single number, then the sequence diverges. If a sequence converges, then the limit of the sequence is found by
$$ \lim_{n \rightarrow ∞} a_n $$
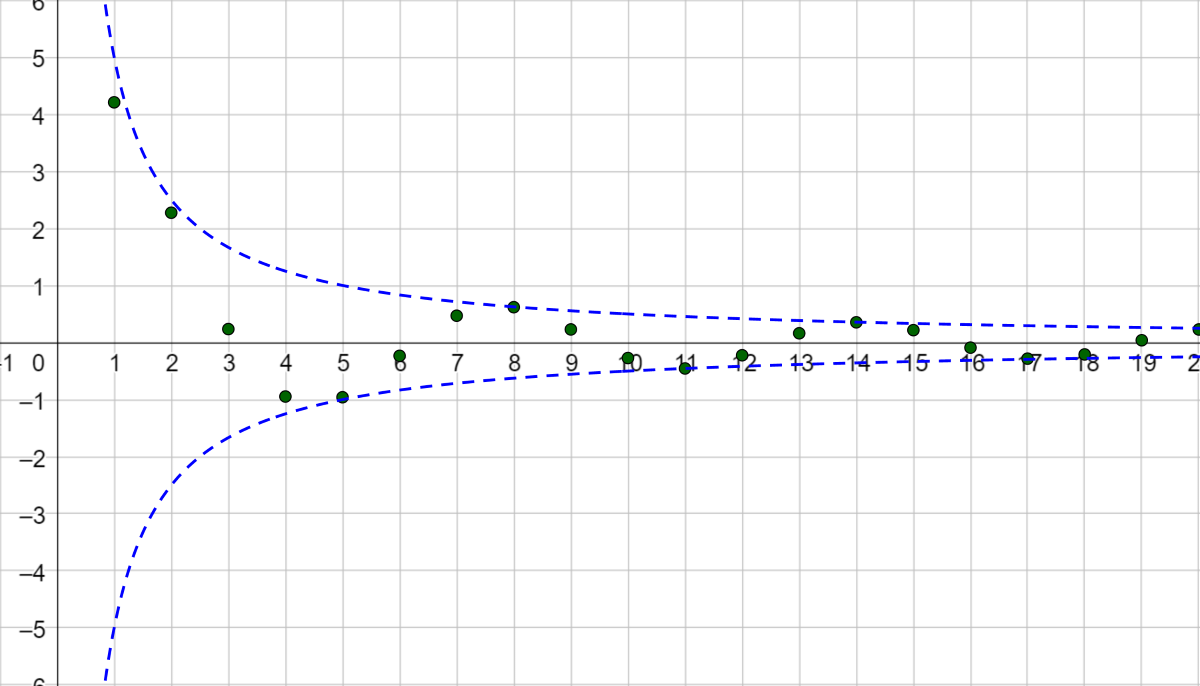
$$ \lim_{n \rightarrow ∞} a_n $$
If the limit exists, then the sequence converges.
If the limit does not exist, then the sequence diverges.
Find the limit of the sequence \(a_n = \frac{(n + 2)(6n - 5)}{2 - 3n + 3n^2}\) and state whether it converges or diverges.
Solution
Find the limit of the sequence as n approaches infinity.
$$ \lim_{n \rightarrow ∞} \frac{(n + 2)(6n - 5)}{2 - 3n + 3n^2} $$
Use the shortcut method to find the limit. Multiply the numerator to find its degree and rearrange the denominator with decreasing exponents.
$$ \lim_{n \rightarrow ∞} \frac{6n^2 + 7n - 10}{3n^2 - 3n + 2} $$
N = 2; D = 2
N = D, so the limit is the leading coefficients. \(\displaystyle \lim_{n \rightarrow ∞} \frac{6n^2 + 7n - 10}{3n^2 - 3n + 2} = \frac{6}{3} = 2\).
Since the limit of the sequence exists, it converges to 2.
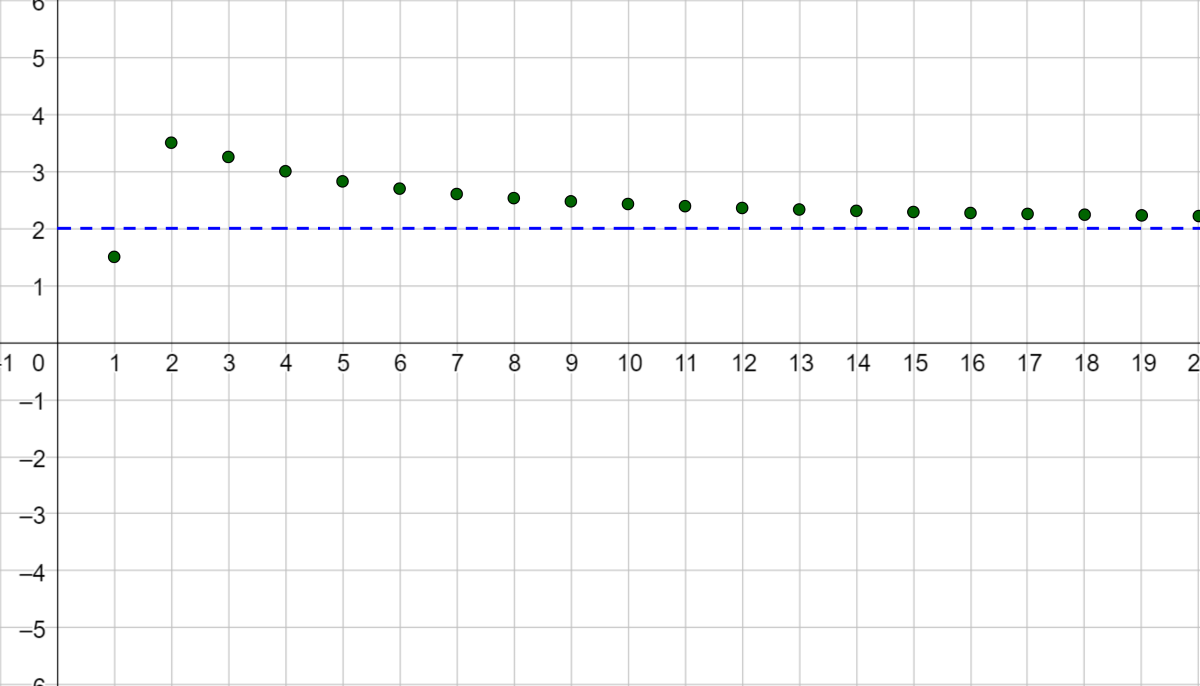
Find the limit of the sequence \(a_n = \frac{4}{n^3} \cdot \left[\frac{n(n+1)(2n+1)}{6}\right]\) and state whether it converges or diverges.
Solution
Find the limit of the sequence as n approaches infinity.
$$ \lim_{n \rightarrow ∞} \frac{4}{n^3} \cdot \left[\frac{n(n+1)(2n+1)}{6}\right] $$
Use the shortcut method to find the limit. Multiply the numerator and denominator to find their degrees.
$$ \lim_{n \rightarrow ∞} \frac{4}{n^3} \cdot \left[\frac{2n^3 + 3n^2 + n}{6}\right] $$
$$ \lim_{n \rightarrow ∞} \frac{8n^3 + 12n^2 + 4n}{6n^3} $$
N = 3; D = 3
N = D, so the limit is the leading coefficients. \(\displaystyle \lim_{n \rightarrow ∞} \frac{8n^3 + 12n^2 + 4n}{6n^3} = \frac{8}{6} = \frac{4}{3}\).
Since the limit of the sequence exists, it converges to \(\frac{4}{3}\).
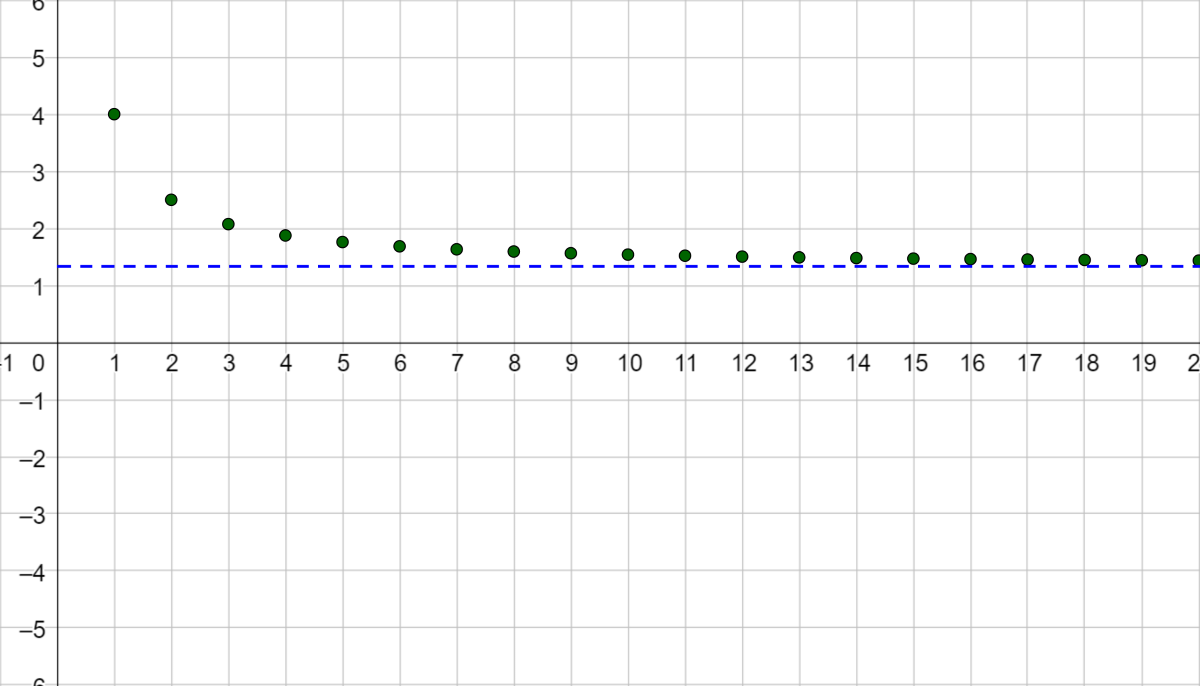
Find the limit of the sequence \(a_n = \frac{3}{n^2} \cdot \left[\frac{n(n+1)}{2}\right]\) and state whether it converges or diverges.
Answer
The sequences converges to \(\frac{3}{2}\).
If f(x) is a rational function, then \(\displaystyle \lim_{x \rightarrow ∞} f(x)\) is found by
Let N = degree of the numerator
Let D = degree of the denominator
$$ \lim_{n \rightarrow ∞} a_n $$
If the limit exists, then the sequence converges.
If the limit does not exist, then the sequence diverges.
Helpful videos about this lesson.