Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
For God so loved the world that he gave his one and only Son, that whoever believes in him shall not perish but have eternal life. John 3:16 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.4.2, PC.6.4
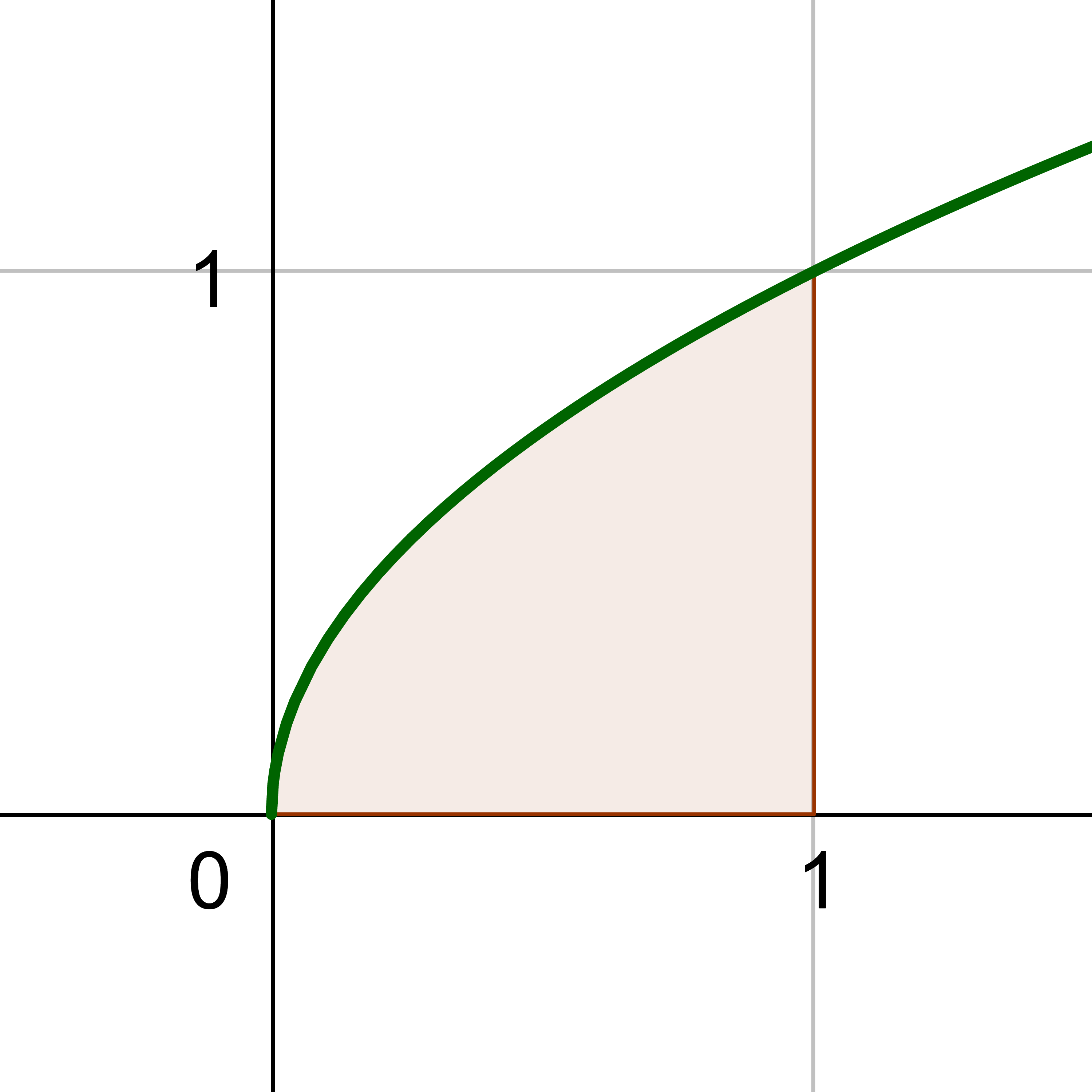
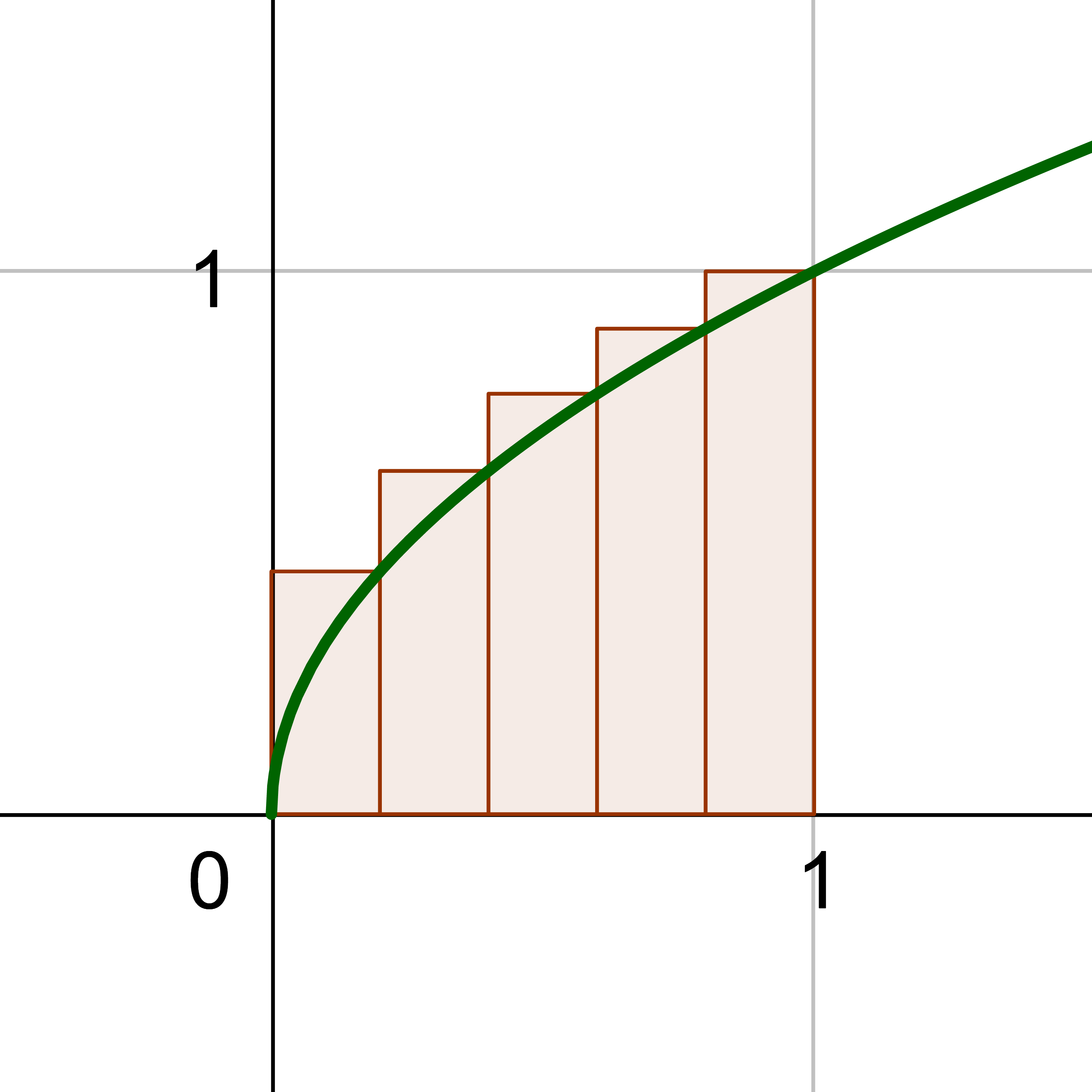
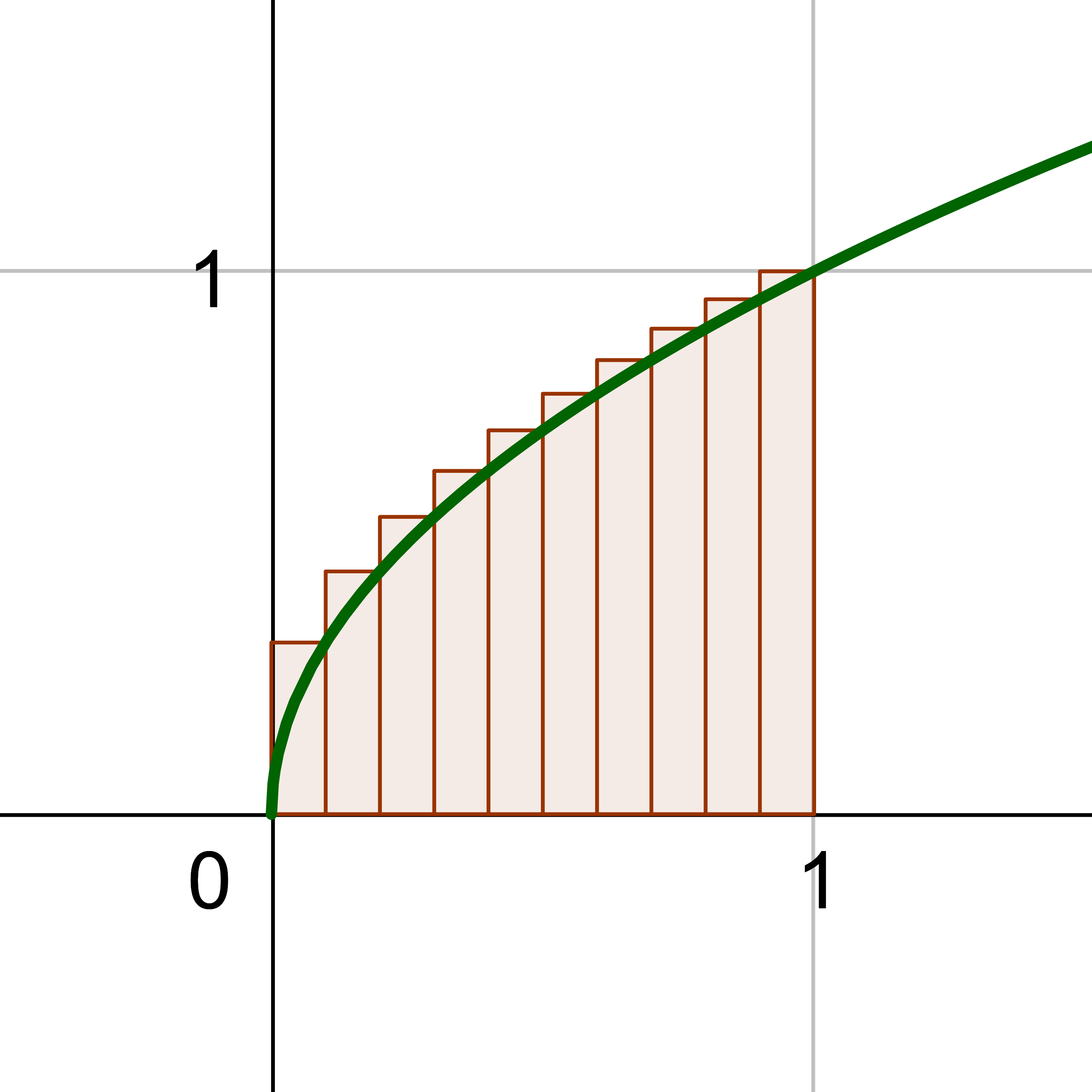
The first part of calculus is the derivative. The second major part of calculus is finding the area between a curve and the x-axis and in the first picture of figure 1. This is the opposite of a derivative. To estimate the area, several rectangles of equal width can be drawn between the x-axis and the function. Then the areas of each rectangle are added together. Notice in the other two pictures in figure 1 that when more rectangles are used, the narrower each one is, and the better the estimate of the area. Thus if we let the number of rectangles approach infinity, the estimated area should approach the exact area.
Before we go further, we will review properties of sums.
Associative Property
\(\displaystyle \sum_{i=1}^{n} (a_i ± b_i) = \sum_{i=1}^{n} a_i ± \sum_{i=1}^{n} b_i\)
Distributive Property
\(\displaystyle \sum_{i=1}^{n} ka_i = k \sum_{i=1}^{n} a_i\)
Sum Formulas
Find the limit of \(\displaystyle \sum_{i=1}^{n} \frac{i + 2}{n^2}\) as n approaches infinity.
Solution
The problems asks us to evaluate the following limit.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \frac{i + 2}{n^2} $$
Since there is a single denominator, split the fraction into two separate fractions.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \left(\frac{i}{n^2} + \frac{2}{n^2}\right) $$
Apply the associative property.
$$ \lim_{n \rightarrow ∞} \left(\sum_{i=1}^{n} \frac{i}{n^2} + \sum_{i=1}^{n} \frac{2}{n^2}\right) $$
Apply the distributive property. i is the index of summation, so factor out everything that is not an i.
$$ \lim_{n \rightarrow ∞} \left(\frac{1}{n^2} \sum_{i=1}^{n} i + \frac{2}{n^2} \sum_{i=1}^{n} 1\right) $$
Apply the sum formulas.
$$ \lim_{n \rightarrow ∞} \left(\frac{1}{n^2} \left[\frac{n^2 + n}{2}\right] + \frac{2}{n^2} \left[ n \right]\right) $$
$$ \lim_{n \rightarrow ∞} \left(\left[\frac{n^2 + n}{2n^2}\right] + \left[\frac{2n}{n^2}\right]\right) $$
Split into two separate limits.
$$ \lim_{n \rightarrow ∞} \left[\frac{n^2 + n}{2n^2}\right] + \lim_{n \rightarrow ∞} \left[\frac{2n}{n^2}\right] $$
Evaluate the limits.
$$ = \frac{1}{2} + 0 $$
$$ = \frac{1}{2} $$
Find the limit of \(\displaystyle \sum_{i=1}^{n} \frac{i^2 - 1}{n^3}\) as n approaches infinity.
Answer
\(\frac{1}{3}\)
A definite integral of a function is the area between the curve and the x-axis between two x-values a and b. To calculate this area, imagine drawing rectangles of equal width with their bottom on the x-axis and their top, right corner on the curve as in figure 2. The area would approximately be the area of the rectangles. However, if the number of rectangles was increased, each one would be thinner and the estimate of the area would be better. So, let there be an infinite number of rectangles.
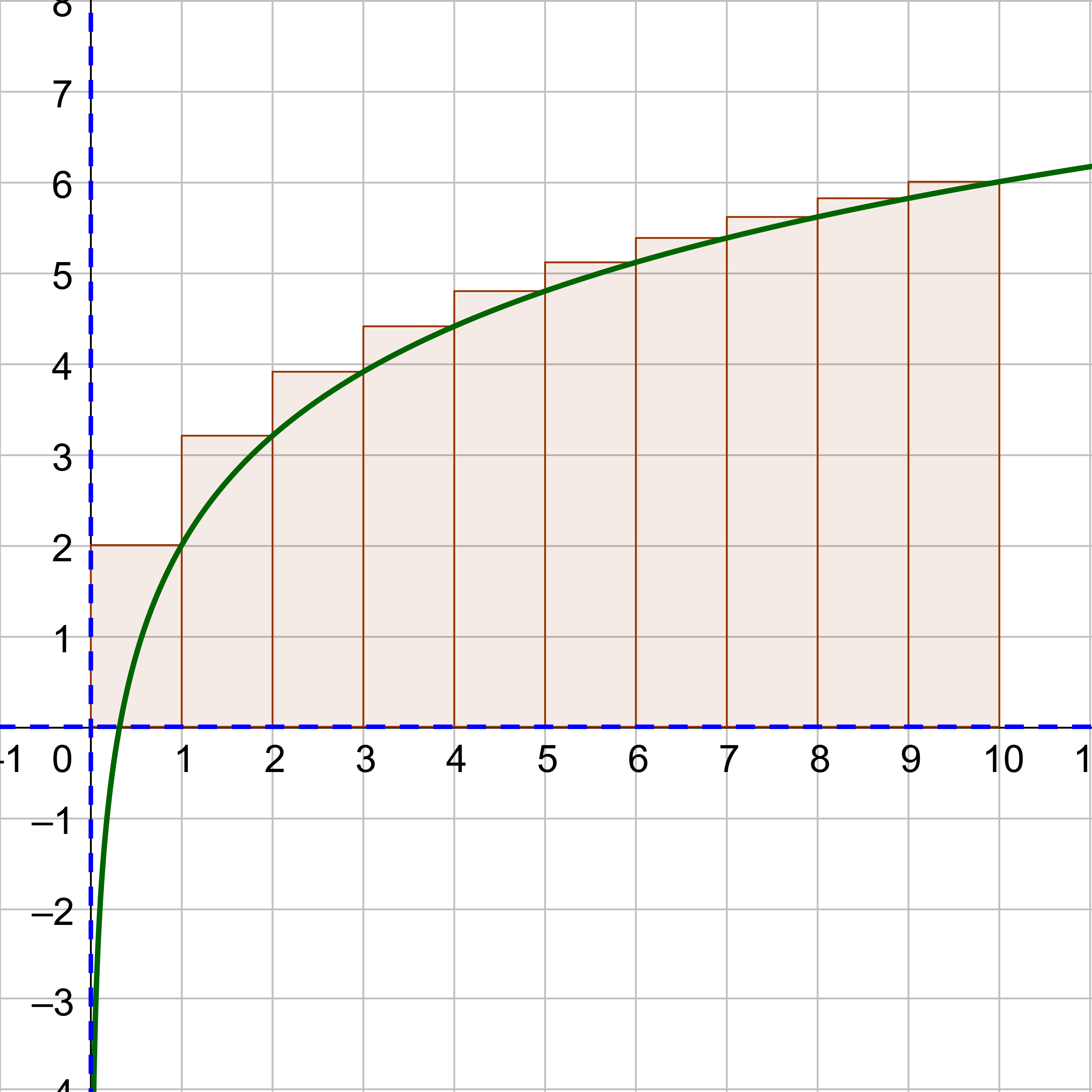
The area of a rectangle is length × width.
Area = ℓw
The widths of the rectangles are the distance between a and b divided by the number of rectangles n.
$$ w = \frac{b-a}{n} $$
In this case, the length is the height of the rectangle which is f(x). The x-value will the be the right side of the rectangle. This is a + the width of the rectangle.
$$ \ell = f\left(a + \frac{b-a}{n}\right) $$
So the area of the first rectangle becomes
$$ Area = f\left(a + \frac{b-a}{n}\right) \cdot \frac{b-a}{n} $$
Add, or sum, the rectangles together. The index of summation will be i, and insert this into the height to indicate which rectangle is being added.
$$ Area = \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Finally, take the limit as n approaches infinity.
$$ Area = \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Integral notation for the area between a and b between the curve and the x-axis is
$$ \int_{a}^{b} f(x) dx $$
The area between f(x) and the x-axis between a and b is
$$ \int_{a}^{b} f(x) dx $$
And it is calculated by
$$ = \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Integrals are the opposites of derivatives. For example, the derivative of a displacement function gives a velocity function. The integral of a velocity function gives the displacement function. So, the integral of a derivative, or the derivative of the integral, gives the original function. Of course this lesson is only exploring integrals that give specific areas and not functions. Those will be reserved for calculus.
Note: if the area is below the x-axis, it is negative. Area above the x-axis is positive.
Find the area bounded by f(x) = x2 between x = 0 and x = 1.
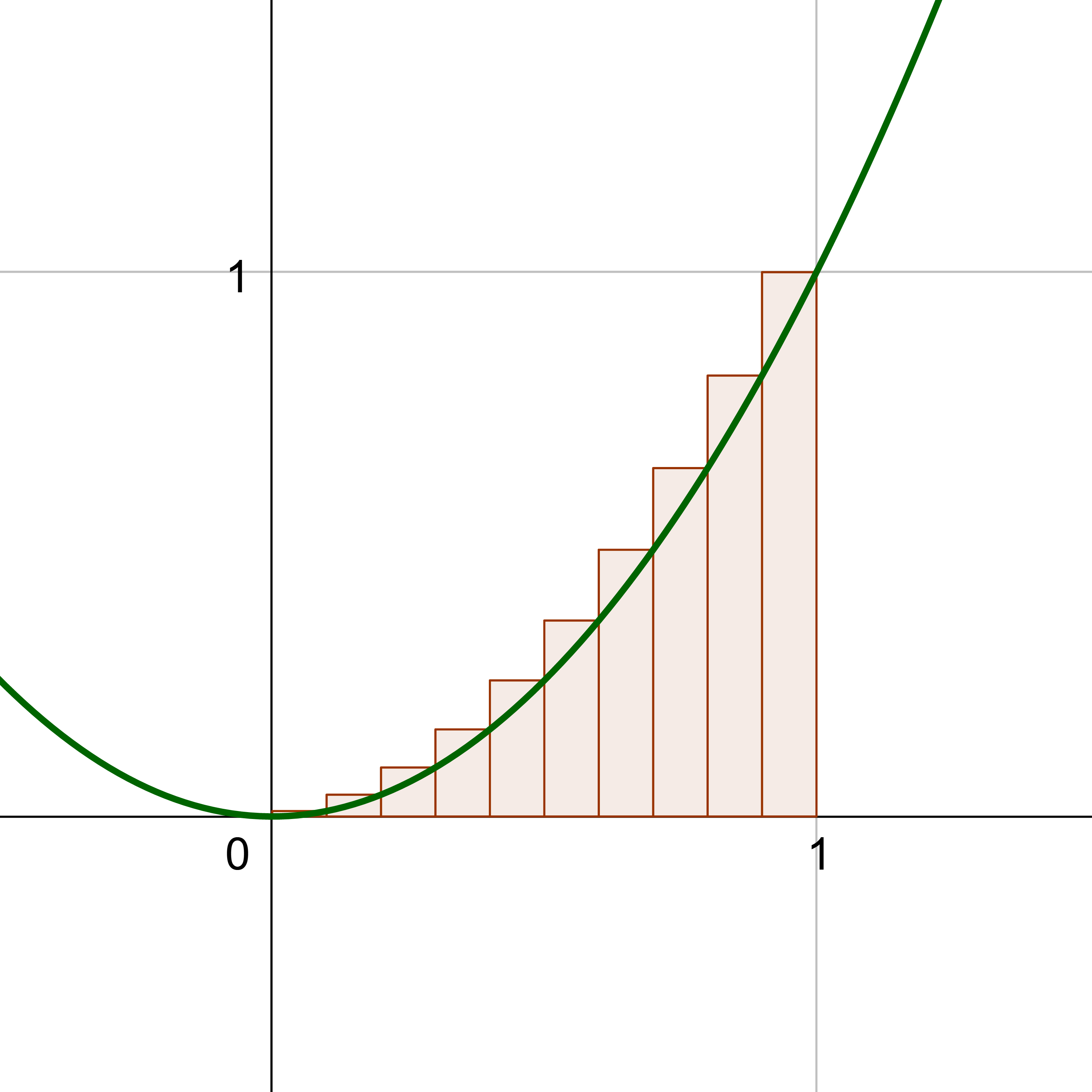
Solution
Start with the area (integral) formula.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Plug in a = 0 and b = 1 because those are the x-value boundaries given in the problem. Then simplify.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(0 + \frac{1-0}{n} i\right) \cdot \frac{1-0}{n} $$
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(\frac{1}{n} i\right) \cdot \frac{1}{n} $$
Find and plug in \(f\left(\frac{1}{n} i\right)\) given that f(x) = x2.
$$ f\left(\frac{1}{n} i\right) = \left(\frac{1}{n} i\right)^2 = \frac{1}{n^2} i^2 $$
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \color{blue}{\frac{1}{n^2} i^2} \cdot \frac{1}{n} $$
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \frac{1}{n^\color{blue}{3}} i^2 $$
Apply the distributive property to factor out everything that is not an i.
$$ \lim_{n \rightarrow ∞} \color{blue}{\frac{1}{n^3}}\sum_{i=1}^{n} i^2 $$
Apply the sum formula for i2 and simplify.
$$ \lim_{n \rightarrow ∞} \frac{1}{n^3} \color{blue}{\frac{2n^3 + 3n^2 + n}{6}} $$
$$ \lim_{n \rightarrow ∞} \frac{2n^3 + 3n^2 + n}{6\color{blue}{n^3}} $$
Evaluate the limit. The degrees of the numerator and denominator are the same, both 3, so the limit is the leading coefficients.
$$ = \frac{2}{6} = \frac{1}{3} $$
Evaluate \(\int_{1}^{2} (x^2 - 3x) \, \mathrm{d}x\).
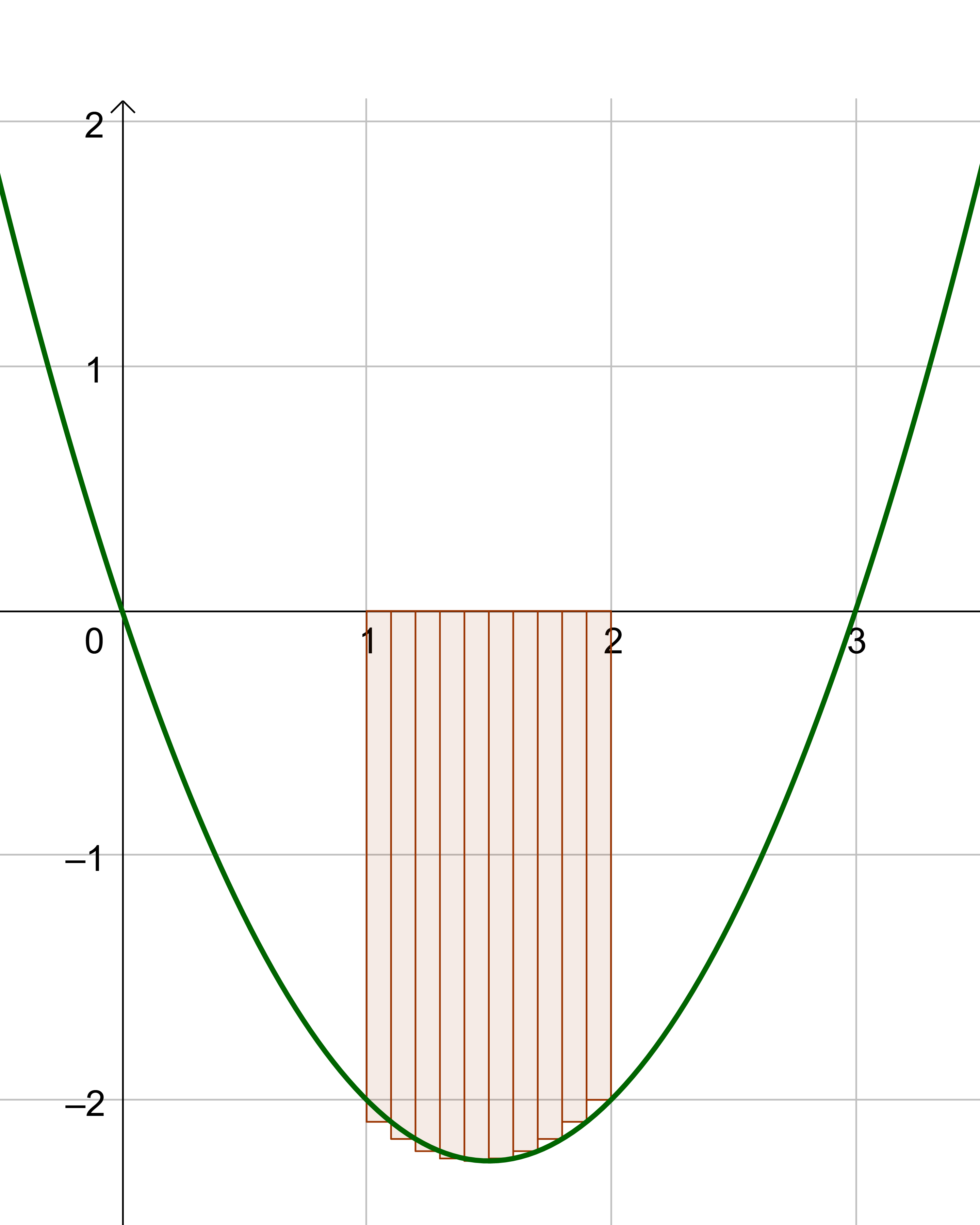
Solution
Start with the area (integral) formula.
$$ \int_{a}^{b} f(x) dx = \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Plug in a = 1 and b = 2 because those are the x-value boundaries given in the problem. Then simplify.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(1 + \frac{2-1}{n} i\right) \cdot \frac{2-1}{n} $$
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(1 + \frac{1}{n} i\right) \cdot \frac{1}{n} $$
Find \(f\left(1 + \frac{1}{n} i\right)\) given that f(x) = x2 − 3x.
$$ f\left(1 + \frac{1}{n} i\right) = \left(1 + \frac{1}{n} i\right)^2 - 3\left(1 + \frac{1}{n} i\right) $$
$$ = 1 + \frac{2}{n}i + \frac{1}{n^2}i^2 - 3 - \frac{3}{n}i $$
$$ = \frac{1}{n^2}i^2 - \frac{1}{n}i - 2$$
Plug this into the integral calculation.
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \color{blue}{\left(\frac{1}{n^2}i^2 - \frac{1}{n}i - 2\right)} \cdot \frac{1}{n} $$
Distribute the \(\frac{1}{n}\).
$$ \lim_{n \rightarrow ∞} \sum_{i=1}^{n} \left(\frac{1}{n^\color{blue}{3}}i^2 - \frac{1}{n^\color{blue}{2}}i - \frac{2}{\color{blue}{n}}\right) $$
Apply the associative property.
$$ \lim_{n \rightarrow ∞} \left(\color{blue}{\sum_{i=1}^{n}}\frac{1}{n^3}i^2 - \color{blue}{\sum_{i=1}^{n}}\frac{1}{n^2}i - \color{blue}{\sum_{i=1}^{n}}\frac{2}{n}\right) $$
Apply the distributive property to factor out all non-i's.
$$ \lim_{n \rightarrow ∞} \left(\color{blue}{\frac{1}{n^3}}\sum_{i=1}^{n}i^2 - \color{blue}{\frac{1}{n^2}}\sum_{i=1}^{n}i - \color{blue}{\frac{2}{n}}\sum_{i=1}^{n} 1\right) $$
Apply sum formulas.
$$ \lim_{n \rightarrow ∞} \left(\frac{1}{n^3}\color{blue}{\frac{2n^3 + 3n^2 + n}{6}} - \frac{1}{n^2}\color{blue}{\frac{n^2 + n}{2}} - \frac{2}{n}\color{blue}{n}\right) $$
$$ \lim_{n \rightarrow ∞} \left(\frac{2n^3 + 3n^2 + n}{6\color{blue}{n^3}} - \frac{n^2 + n}{2\color{blue}{n^2}} - \frac{2\color{blue}{n}}{n}\right) $$
Use the property of limits to split this into three limits.
$$ \color{blue}{\lim_{n \rightarrow ∞}}\frac{2n^3 + 3n^2 + n}{6n^3} - \color{blue}{\lim_{n \rightarrow ∞}}\frac{n^2 + n}{2n^2} - \color{blue}{\lim_{n \rightarrow ∞}}\frac{2n}{n} $$
Evaluate the limits. All three have the same degree in their numerator and denominator, so the limits are all the leading coefficients.
$$ = \frac{2}{6} - \frac{1}{2} - \frac{2}{1} $$
$$ = \frac{2}{6} - \frac{3}{6} - \frac{12}{6} $$
$$ = -\frac{13}{6} $$
Evaluate \(\int_{0}^{2} \! x^3 \, \mathrm{d}x\).
Answer
4
Associative Property
\(\displaystyle \sum_{i=1}^{n} (a_i ± b_i) = \sum_{i=1}^{n} a_i ± \sum_{i=1}^{n} b_i\)
Distributive Property
\(\displaystyle \sum_{i=1}^{n} ka_i = k \sum_{i=1}^{n} a_i\)
Sum Formulas
The area between f(x) and the x-axis between a and b is
$$ \int_{a}^{b} f(x) dx $$
And it is calculated by
$$ = \lim_{n \rightarrow ∞} \sum_{i=1}^{n} f\left(a + \frac{b-a}{n} i\right) \cdot \frac{b-a}{n} $$
Helpful videos about this lesson.