![[change in y over change in x]](../webtexts/slopefor.gif)
Last lesson we introduced correlation and the correlation coefficients of Pearson and Spearman. In this lesson we come up with linear regression equations.
Since the discussion is on linear correlations and the predicted values need to be as close as possible to the data, the equation is called the best-fitting line or regression line. The regression line was named after the work Galton did in gene characteristics that reverted (regressed) back to a mean value. That is, tall parents had children closer to the average.
Slope is an important concept so we will review some important facts here.
slope = m = rise/run = dy/dx
= ![[change in y over change in x]](../webtexts/slopefor.gif)
|
| Parallel lines have equal slopes. |
In summary, if y = mx + b, then m is the slope and b is the y-intercept (i.e., the value of y when x = 0). Often linear equations are written in standard form with integer coefficients (Ax + By = C). Such relationships must be converted into slope-intercept form (y = mx + b) for easy use on the graphing calculator. One other form of an equation for a line is called the point-slope form and is as follows: y - y1 = m(x - x1). The slope, m, is as defined above, x and y are our variables, and (x1, y1) is a point on the line.
An equation of a line can be expressed as y = mx + b or y = ax + b or even y = a + bx. As we see, the regression line has a similar equation. There are a wide variety of reasons to pick one equation form over another and certain disciplines tend to pick one to the exclusion of the other. BE FLEXIBLE both on the order of the terms within the equation and on the symbols used for the coefficients! With the interdisciplinary nature of a lot of research these days, conflict between differing notations should be minimized.
|
y = ß0 + ß1x where y, ß0, and ß1 represents population statistics. If a cap appears above the variable, then they probably represent sample statistics. Remember x is our independent variable for both the line and the data. |
The y-intercept of the regression line is ß0 and the slope is ß1. The following formulas give the y-intercept and the slope of the equation.
ß0 =
(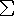 y)( y)(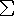 x2) -
( x2) -
(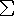 x)( x)(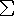 xy) xy) n( 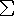 x2) - ( x2) - (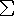 x)2 x)2
|
ß1 =
n(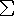 xy) -
( xy) -
(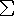 x)( x)(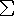 y) y) n( 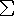 x2) - ( x2) - (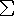 x)2 x)2
|
Notice that the denominators are the same, so that saves calculations. Also, the calculator will have values for certain portions. Another way to write the equation is in point-slope form where the centroid is the point that is always on the line. The centroid is the following ordered pair: (mean of x, mean of y).
|
To keep the y-intercept and slope accurate,
all intermediate steps should be kept to twice as many significant digits (six to ten?) as you want in your final answer (three to five?)! |
There are certain guidelines for regression lines:
The y variable is often termed the criterion variable and the x variable the predictor variable. The slope is often called the regression coefficient and the intercept the regression constant. The slope can also be expressed compactly as ß1= r × sy/sx.
Normally we then predict values for y based on values of x. This still does not mean that y is caused by x. It is still imperative for the researcher to understand the variables under study and the context they operate under before making such an interpretation. Of course, simple algebra also allows one to calculate x values for a given value of y.
Example: Write the regression line for the following points:
| x | y |
|---|---|
| 1 | 4 |
| 3 | 2 |
| 4 | 1 |
| 5 | 0 |
| 8 | 0 |
Solution 1:
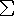 x = 21;
x = 21;
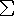 y = 7;
y = 7;
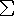 x2 = 115;
x2 = 115;
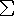 y2 = 21;
y2 = 21;
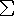 xy = 14
xy = 14
Thus ß0 = [7·115 - 21·14] ÷ [5 · 115 - 212] = 511 ÷ 134 = 3.81
and ß1 = [5·14 - 21·7] ÷ [5 · 115 - 212] = -77 ÷ 134 = -0.575.
Thus the regression line for this example is y = -0.575x + 3.81.
Solution 2:
On your TI-83+ graphing calculator, enter the data into L1 and
L2 and do a LinReg(ax+b) L1, L2 (STAT, CALC, 4)
or LinReg(a+bx) L1, L2 (STAT, CALC, 8).
You should get a screen with
y=ax+b
a=-.5746...
b=3.8134...
r2=.790...
r=.88888...
If the r information is absent, do CATALOG (2nd 0)
DiagnosticOn. ENTRY (2nd ENTER) will bring the command back to the home screen
where another ENTER will execute it.
We thus see that about 79% of the variation in y
is explained by the variation in x.
There is no mathematical difference between the two linear regression forms LinReg(ax+b) and LinReg(a+bx), only different professional groups prefer different notations. Preferred is perhaps too weak a word here. The calculator manufacturer included both forms since neither group was willing to compromise and use the other.
Note the presence on your TI-83+ graphing calculator of several other regression functions as well. Specifically, quadratic (y = ax2 + bx + c), cubic (y = ax3 + bx2 + cx + d), quartic (y = ax4 + bx3 +cx2 + dx + e), exponential (y = abx), and power or variation (y = axb). Thus an easy way to find a quadratic through three points would be to enter the data in a pair of lists then do a quadratic regression on the lists.
What is the Least Squares Property?
Form the distance y - y' between each data point (x, y)
and a potential regression line y' = mx + b.
Each of these differences is known as a residual.
Square these residuals and sum them.
The resulting sum is called the residual sum of squares or SSres.
The line that best fits the data has the least possible value of SSres.
This link has a nice colorful example of these residuals, residual squares, and residual sum of squares.
Example:
Find the Linear Regression line through (3,1), (5,6), (7,8) by brute force.
Solution:
| x | y | y' | y - y' |
|---|---|---|---|
| 3 | 1 | 3m + b | 1 - 3m - b |
| 5 | 6 | 5m + b | 6 - 5m - b |
| 7 | 8 | 7m + b | 8 - 7m - b |
Using the fact that (A + B + C)2 = A2 + B2 + C2 + 2AB + 2AC + 2BC, we can quickly find SSres = 101 + 83m2 + 3b2 - 178m - 30b + 30mb. This expression is quadratic in both m and b. We can rewrite it both ways and then find the vertex for each (which is the minimum since we are summing squares). Remember the vertex of y = ax2 + bx + c is -b/2a.
SSres = 3b2 + (30m - 30)b + (101 + 83m2 - 178m).
SSres = 83m2 + (30b - 178)m + (101 + 3b2 - 30b).
From the first expression we find b = (-30m + 30)/6.
From the second expression we find m = (-30b + 178)/166.
These expressions give us two equations in two unknowns:
5m + b = 5 and
83m + 15b = 89.
These can be solved to obtain m = 7/4 = 1.75 and b = -15/4 = -3.75.
This is how the equations above for ß0
and ß1 were derived, from the general solution
to two general equations for SSres.
This link brings up a Java applet which allows you to add a point to a graph and see what influence it has on a regression line.
This link brings up a Java applet which encourages you to guess the regression line and correlation coefficient for a data set.
s2y•x =
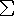 e2/(n - 2). e2/(n - 2).
|
| syY•x = sy sqrt(1-r2) sqrt((n - 1)/(n - 2)). |
| The standard error is small when the correlation is high. This increases the accuracy of prediction. |
When we consider multiple distributions it is often assumed that their standard deviations are equal. This property is called homoscedasticity. We often consider the conditional distribution or distribution of all y scores with the same value of x. If we assume these conditional distributions are all normal and homoscedastic, we can make probabilistic statements about the predicted scores. The standard deviation we use is the standard error calculated above.
| BACK | HOMEWORK | ACTIVITY | CONTINUE |
|---|