Precalculus by Richard Wright
Precalculus by Richard Wright
Pride goes before destruction, a haughty spirit before a fall. Proverbs 16:18 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.5.3


Imagine a function as a vending machine. You insert some money and out comes a bottle of juice. The drink that comes out of the machine is a function of the amount of money that is inserted into the machine. Now imagine a vending machine that works backwards. Something is put into the machine, and it gives out money. In 2009, EcoATM started putting such machines in stores. A used cellphone is put into the backward vending machine, and it gives you cash.
The vending machine and backward vending machine are examples of an inverse relationship. An inverse function interchanges the input and the output. A regular vending machine inputs money and outputs a product such as a phone. An inverse vending machine inputs a product such as a phone and outputs money.
Imagine you are going to travel to Canada for a weekend of hiking, but you would like nice weather. You check the weather forecast, but it is given in degrees Celsius. Being an American, you are used to degree Fahrenheit. But you do remember the conversion from Fahrenheit to Celsius.

$$ C = \frac{5}{9}(F - 32) $$
You start looking at the first day. To find the temperature in Fahrenheit, you decide to plug in Friday's high of 12°C and solve for F.
$$ 12 = \frac{5}{9}(F - 32) $$
$$ \frac{108}{5} = F - 32 $$
$$ F = \frac{108}{5} + 32 ≈ 53.6°F $$
Slightly cool, but a decent temperature for a nice hike. You start to work on Friday night's temperature, but then notice that you would have to do the same algebra steps for each of the six temperatures. It would be easier to solve the formula for F first, then simply plug in the numbers.
$$ C = \frac{5}{9}(F - 32) $$
$$ \frac{9}{5}C = F - 32 $$
$$ F = \frac{9}{5}C + 32 $$
Now you can just plug in the temperatures in Celsius and get the corresponding temperatures in Fahrenheit. This new formula for converting Celsius to Fahrenheit is the inverse of the Fahrenheit to Celsius formula. Inverse functions switch the inputs and outputs.
If the function is named in function notation, f(x), then the inverse function is named f−1(x) which is read "inverse f of x." Beware the −1 is not an exponent and does not mean \(\frac{1}{f(x)}\) because that is the reciprocal and not the inverse.
Inverses are a type of opposite and undo each other. The inverse cancels out the original leaving only the identity function, x.
(f−1 ∘ f)(x) = f−1(f(x)) = x
Some functions do not have inverse functions. Only functions where each input is paired with a unique output have inverse functions. In these one-to-one functions, each x is paired with only one y, and each y in the range is paired with only one x.
If for a particular one-to-one function f(5) = −2 and f(10) = 23, what are the corresponding input and output values for the inverse function?
Solution
The inverse function switches the input and output quantities, so if
f(5) = −2, then f−1(−2) = 5
f(10) = 23, then f−1(23) = 10
f(x) and g(x) are inverses if either f(g(x)) = x or g(f(x)) = x.
If either statement is true, then both are true, and g = f−1 and f = g−1. If either statement is false, then both are false.
If \(f(x) = \frac{2}{x-3}\) and \(g(x) = \frac{2}{x} + 3\), is g = f−1?
Solution
To test whether two functions are inverses, find the composition of them. If the composition equals x, then they are inverses.
$$ f(g(x)) = \frac{2}{\left(\frac{2}{x} + 3\right) - 3} $$
The threes cancel out.
$$ = \frac{2}{\frac{2}{x}} $$
Divide fractions by multiplying by the reciprocal.
$$ = \frac{2}{1}\frac{x}{2} $$
The twos cancel out.
$$ = x $$
Since the composition equals x, then the functions are inverses.
If f(x) = 2x2 and \(g(x) = \sqrt{2x}\), is g = f−1?
Solution
To test whether two functions are inverses, find the composition of them. If the composition equals x, then they are inverses.
$$ f(g(x)) = 2(\sqrt{2x})^2 $$
The square and the square root cancel out.
= 2(2x)
Simplify.
= 4x
Since the composition does not equals x, then the functions are not inverses.
If f(x) = (x + 2)3 and \(g(x) = \sqrt[3]{x} - 2\), is g = f−1?
Answer
Yes
If \(f(x) = \frac{1}{x^2 + 3}\) and \(g(x) = \sqrt{\frac{1}{x} - 3}\), is g = f−1?
Answer
Yes
Inverse functions switch the input and output, so the domain and range are also switched. The domain of f becomes the range of f−1, and the range of f becomes the domain of f−1.
When a function has no inverse function because it is not one-to-one, it is possible to create a new function where that new function on a limited domain does have an inverse function. For example, the inverse of \(f(x) = \sqrt{x}\) is f−1 = x2, because a square “undoes” a square root. But the square is only the inverse of the square root on the domain [0, ∞), since that is the range of \(f(x) = \sqrt{x}\).
From the other side of the same problem, starting with the square (parent quadratic) function f(x) = x2. There is a problem creating the inverse, because for every given output of the quadratic function, there are two corresponding inputs (except when the input is 0). For example, the output 9 from the quadratic function corresponds to the inputs 3 and −3. But an output from a function is an input to its inverse; if this inverse input corresponds to more than one inverse output (input of the original function), then the “inverse” is not a function at all! To put it differently, the quadratic function is not a one-to-one function; it fails the horizontal line test, so it does not have an inverse function. In order for a function to have an inverse, it must be a one-to-one function.
To determine if a function is one-to-one and has an inverse function, use the horizontal line test. It says that a function is one-to-one if no horizontal line touches the graph more than once.
In many cases, if a function is not one-to-one, it can still be restricted to a part of its domain on which it is one-to-one. For example, the restricted version of the square function f(x) = x2 with its domain limited to [0, ∞) is a one-to-one function (it passes the horizontal line test) and which has an inverse (the square-root function).
The range of a function f(x) is the domain of the inverse function f−1(x).
The domain of f(x) is the range of f−1(x).
If the domain of the original function needs to be restricted to make it one-to-one, then this restricted domain becomes the range of the inverse function.
Inverses switch the x and y-coordinates. To find an inverse function, start by rewriting the f(x) as y. Then interchange the x's and the y's. Next, solve for y. Finally, rewrite the y as f−1(x).
The speed of sound in air in meters per second is a function of temperature. The function is \(v(T) = 331\sqrt{\frac{T}{273}}\) where T is the temperature in Kelvin. Find the inverse of the function.
Solution
Start by rewriting the equation so that it is not in function notation.
$$ v(T) = 331\sqrt{\frac{T}{273}} $$
$$ v = 331\sqrt{\frac{T}{273}} $$
Usually, the two variables would be interchanged in this step, but since they represent actual quantities, they will not be switched.
Now solve for the other variable, T.
$$ \frac{v}{331} = \sqrt{\frac{T}{273}} $$
$$ \left(\frac{v}{331}\right)^2 = \frac{T}{273} $$
$$ 273\left(\frac{v}{331}\right)^2 = T $$
$$ T = 273\left(\frac{v}{331}\right)^2 $$
T = 0.00249v2
Find the inverse of \(f(x)= \frac{3}{x + 1} - 2\).
Solution
Start by rewriting the equation so that it is not in function notation.
$$ f(x) = \frac{3}{x + 1} - 2 $$
$$ y = \frac{3}{x + 1} - 2 $$
Interchanged in the x and the y.
$$ x = \frac{3}{y + 1} - 2 $$
Now solve for y.
$$ x + 2 = \frac{3}{y + 1} $$
$$ (x + 2)(y + 1) = 3 $$
$$ y + 1 = \frac{3}{x + 2} $$
$$ y = \frac{3}{x + 2} - 1$$
Rewrite the equation so that it is in function notation.
$$ f^{-1}(x) = \frac{3}{x + 2} - 1 $$
Find the inverse of the function f(x) = (x + 4)2, x ≤ −4.
Solution
The domain is limited in this problem because function is not one-to-one. The vertex is at (0, −4), so the domain is limited to only one side. Start by rewriting the equation so that it is not in function notation.
f(x) = (x + 4)2, x ≤ −4
y = (x + 4)2, x ≤ −4
Interchange the x and y.
x = (y + 4)2, y ≤ −4
Now solve for y.
$$ ±\sqrt{x} = y + 4, y ≤ −4 $$
$$ ±\sqrt{x} - 4 = y, y ≤ −4 $$
$$ y = ±\sqrt{x} - 4, y ≤ −4 $$
The domain was limited. Now after the x and y were switched, it has become the range. This range is negative, so only the negative from the ± will be used, and the range statement can be dropped.
$$ y = -\sqrt{x} - 4 $$
Rewrite the equation so that it is in function notation.
$$ f^{-1}(x) = -\sqrt{x} - 4 $$
Find the inverse of the function \(f(x) = 2\sqrt{x} + 3\).
Answer
\(f^{-1}(x) = \left(\frac{x - 3}{2}\right)^2\)
Remember from lesson 1-04 that the domain of a function is the part of the x-axis covered by the graph. Because the inverse switches the x and y, the domain of the inverse of a function is the part of the y-axis covered by the graph. The domain and range of inverses are switched. Similarly, a function can be evaluated for an x-value by reading the corresponding y-value from the graph. To evaluate an inverse from the original function's graph, find the input on the y-axis of the graph, then read the corresponding output from the x-axis.
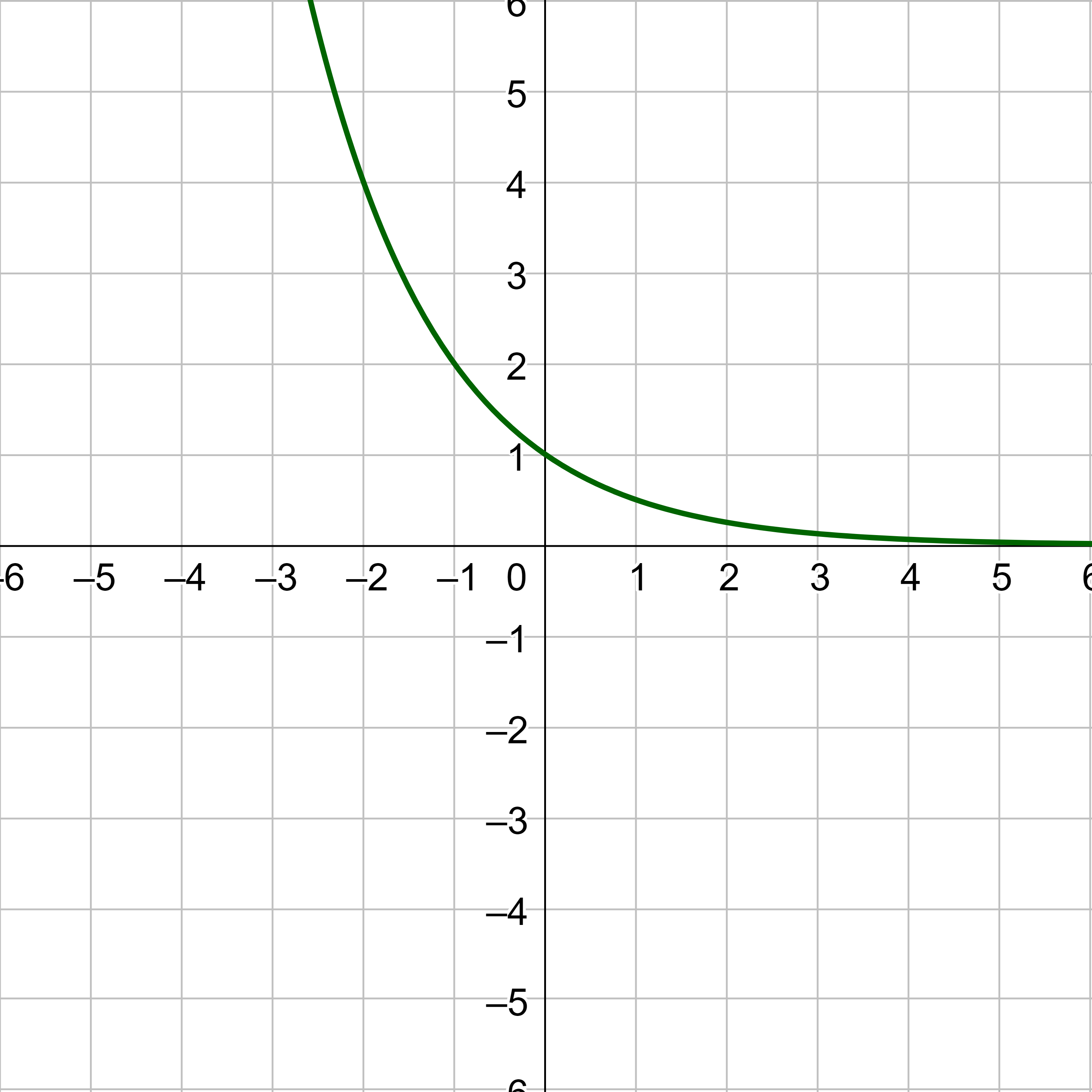
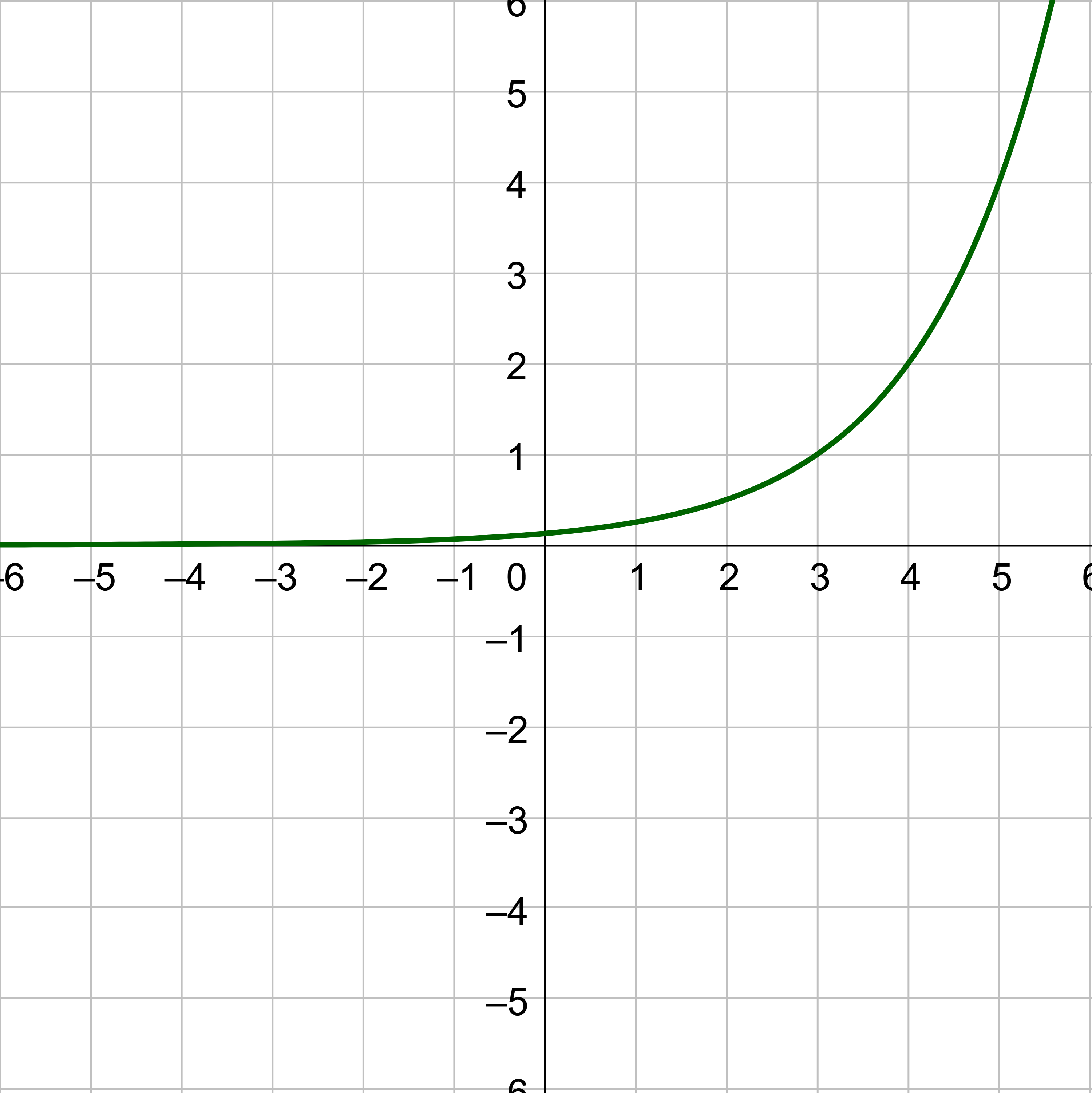
Use the graph of f(x) to find f(3) and f−1(2).
Solution
To evaluate f(3), find 3 on the x-axis and find the corresponding output value on the y-axis. The point (3, 1) indicates that f(3) = 1.
To evaluate f−1(2), remember that the x and y's are switched for the inverse. Find 2 on the y-axis and find the corresponding value x-axis. The point (4, 2) on the original graph means the point on the inverse is (2, 4). It indicates that f−1(2) = 4.
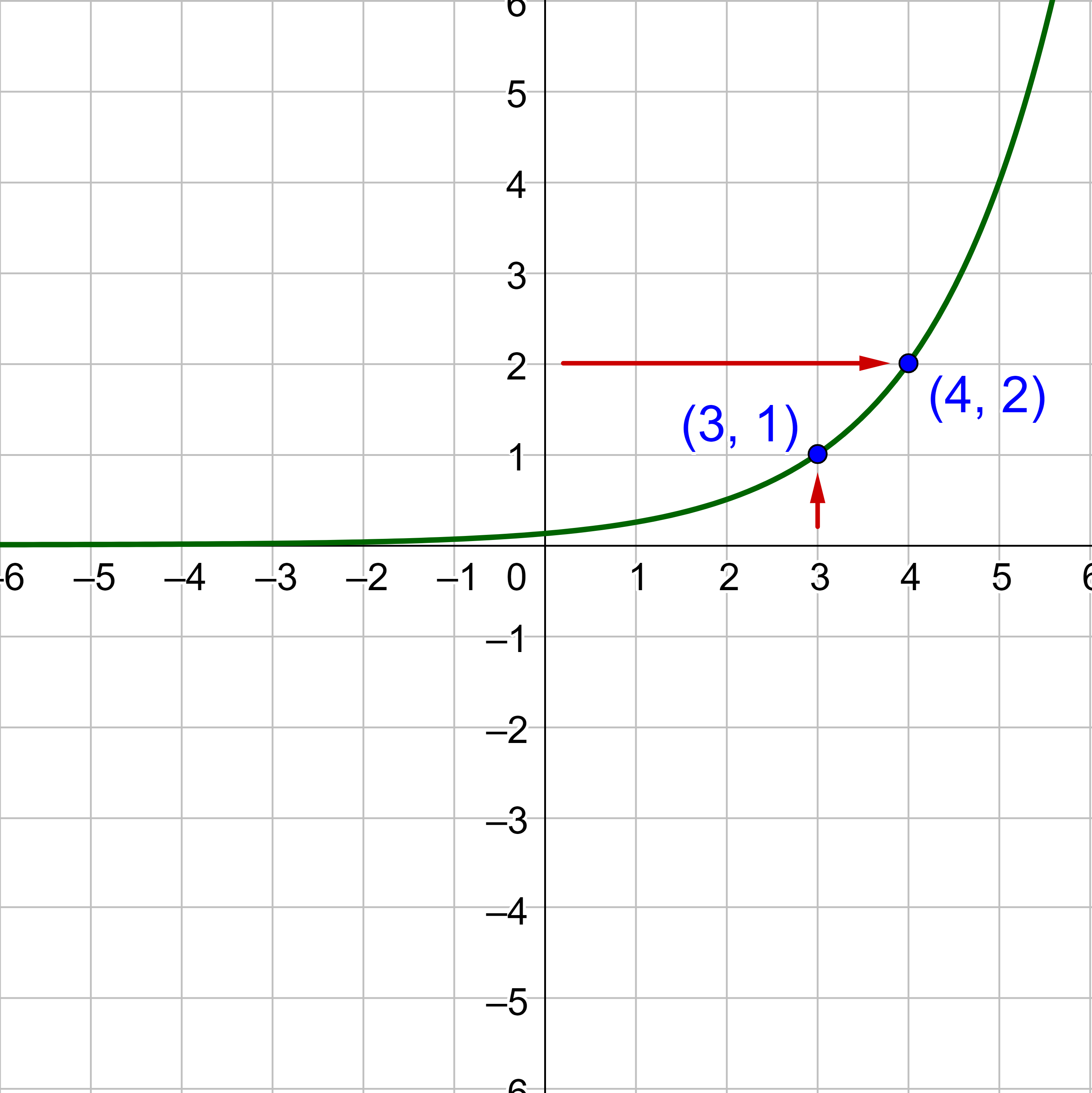
Using the graph in figure 3, (a) find f−1(4), and (b) estimate f−1(3).
Answer
5; 4.6
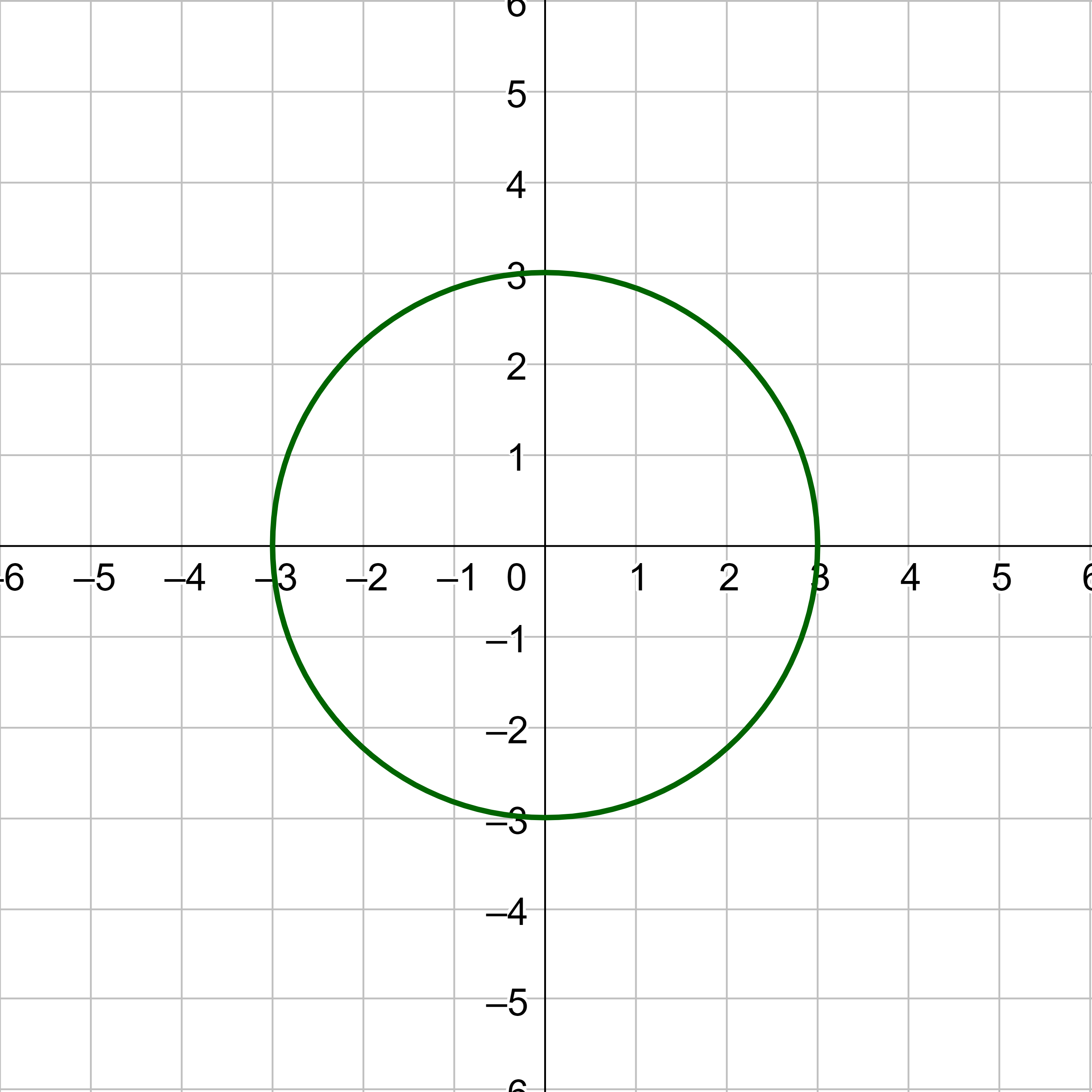
Now it is time to explore the graphs of functions and their inverses further. Use the quadratic function f(x) = x2 restricted to the domain [0, ∞) so that it is one-to-one, and graph it as in figure 5.
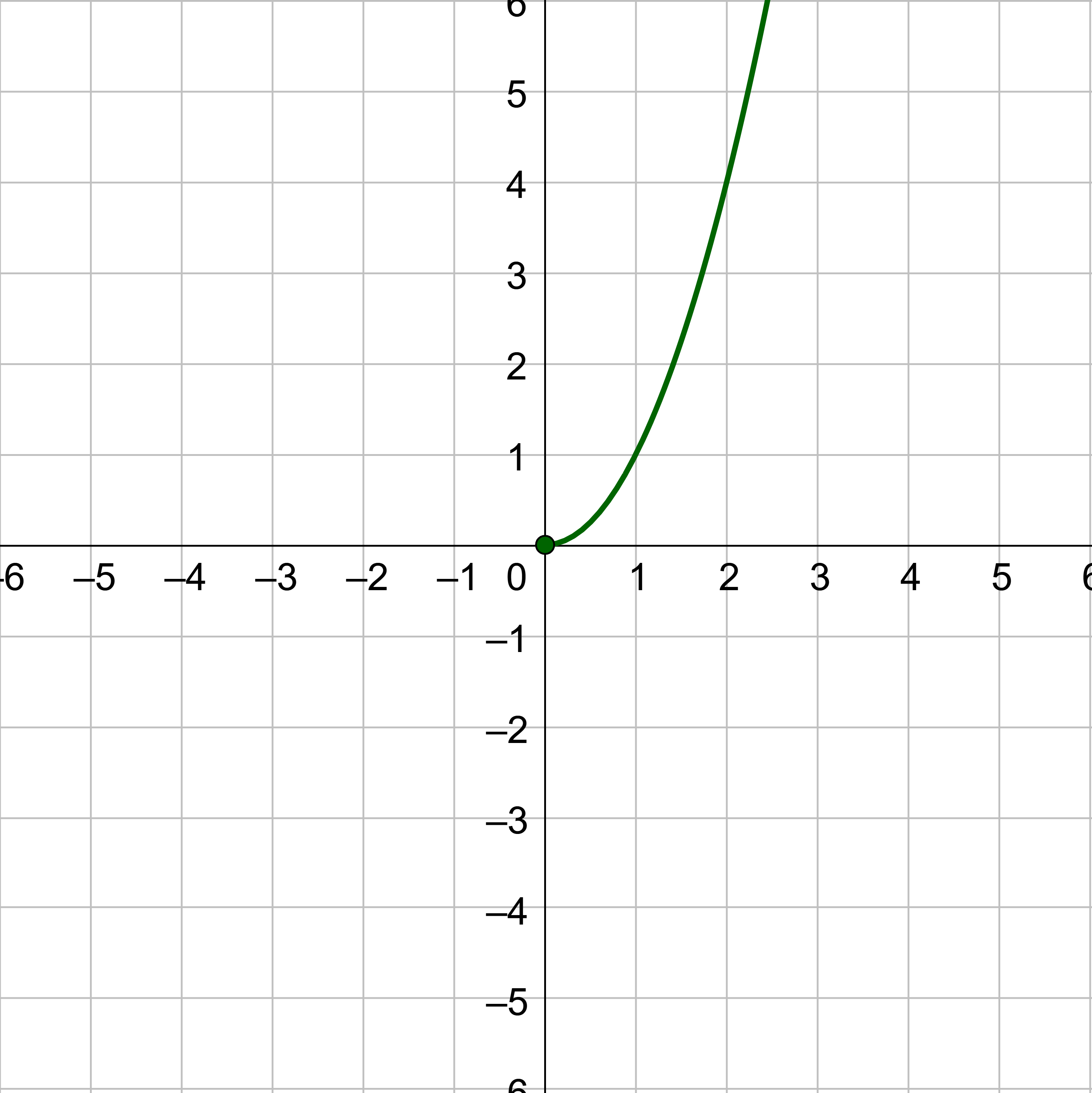
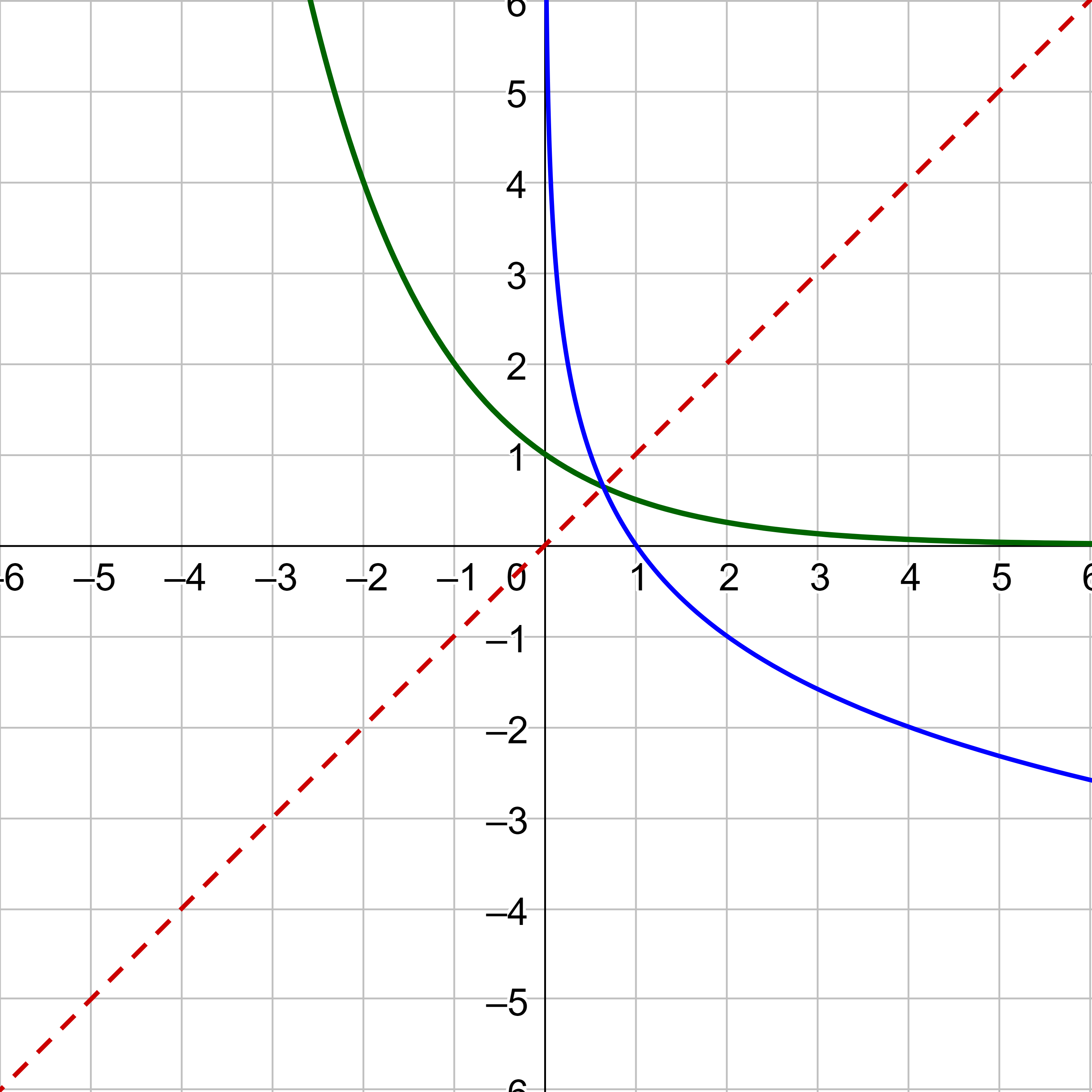
An inverse function, switches the x and y-coordinates. Take each of the points of the graph in figure 5 and exchange the x and y-coordinates so that (2, 4) becomes (4, 2), (3, 9) becomes (9, 3), and so on. This produces the graph in figure 6. Notice that the graph is reflected over the line y = x.
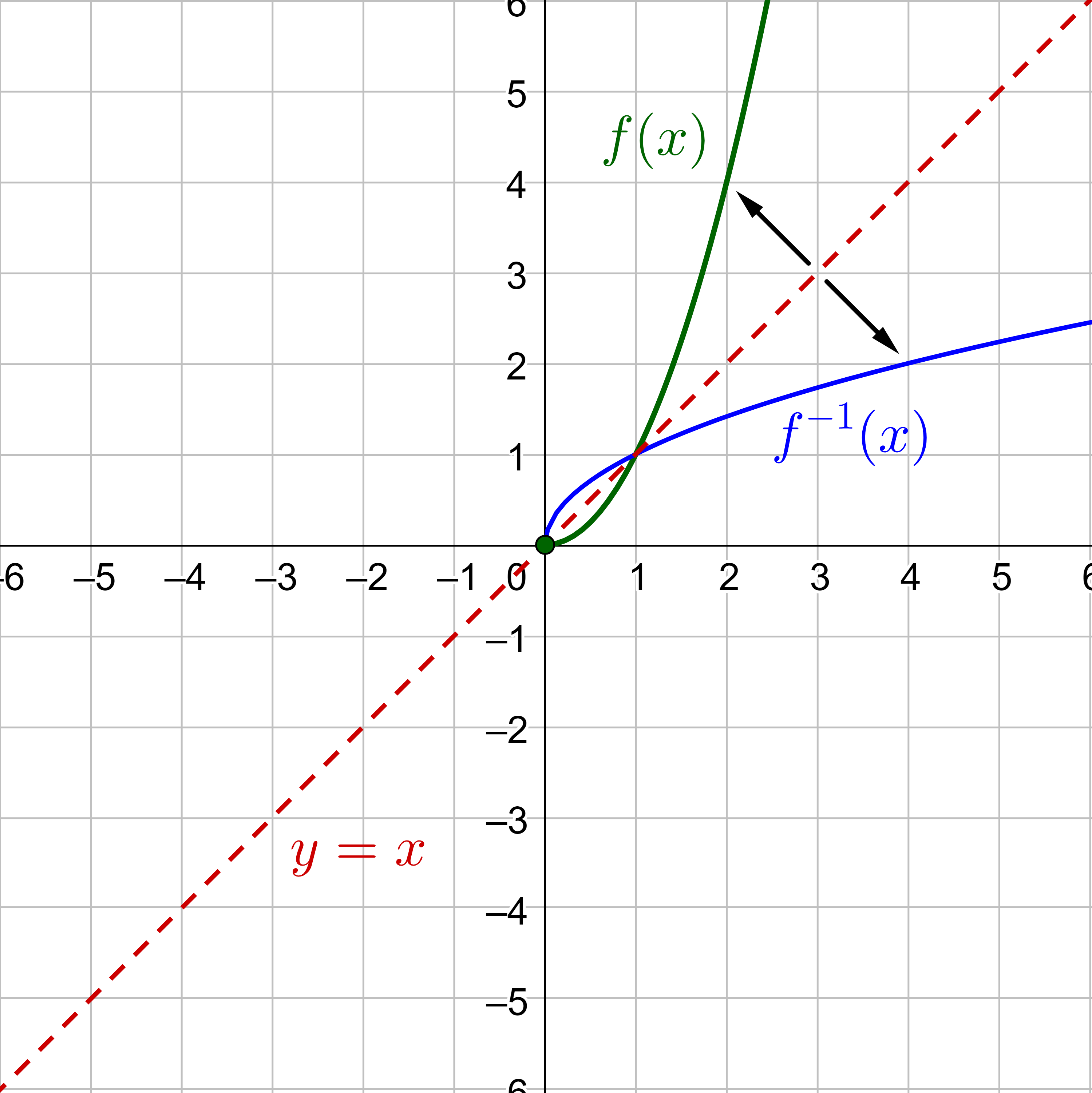
This relationship is true for all inverses. The graphs of a function and its inverse are reflections over the line y = x.
The graph of an inverse is the reflection of f(x) over the line y = x.
To find the inverse graph
OR
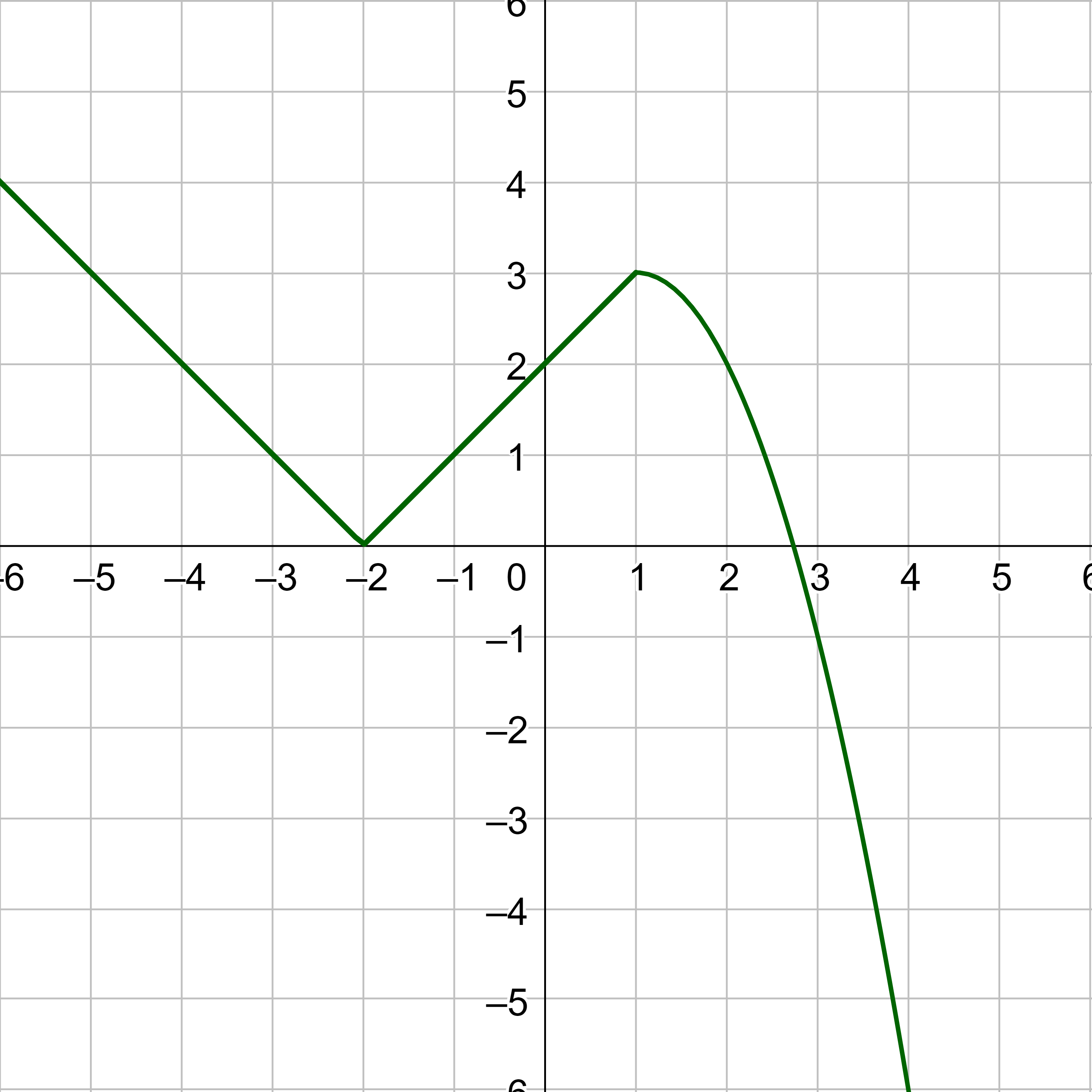
If f(x) is in figure 7, sketch a graph of f−1(x).
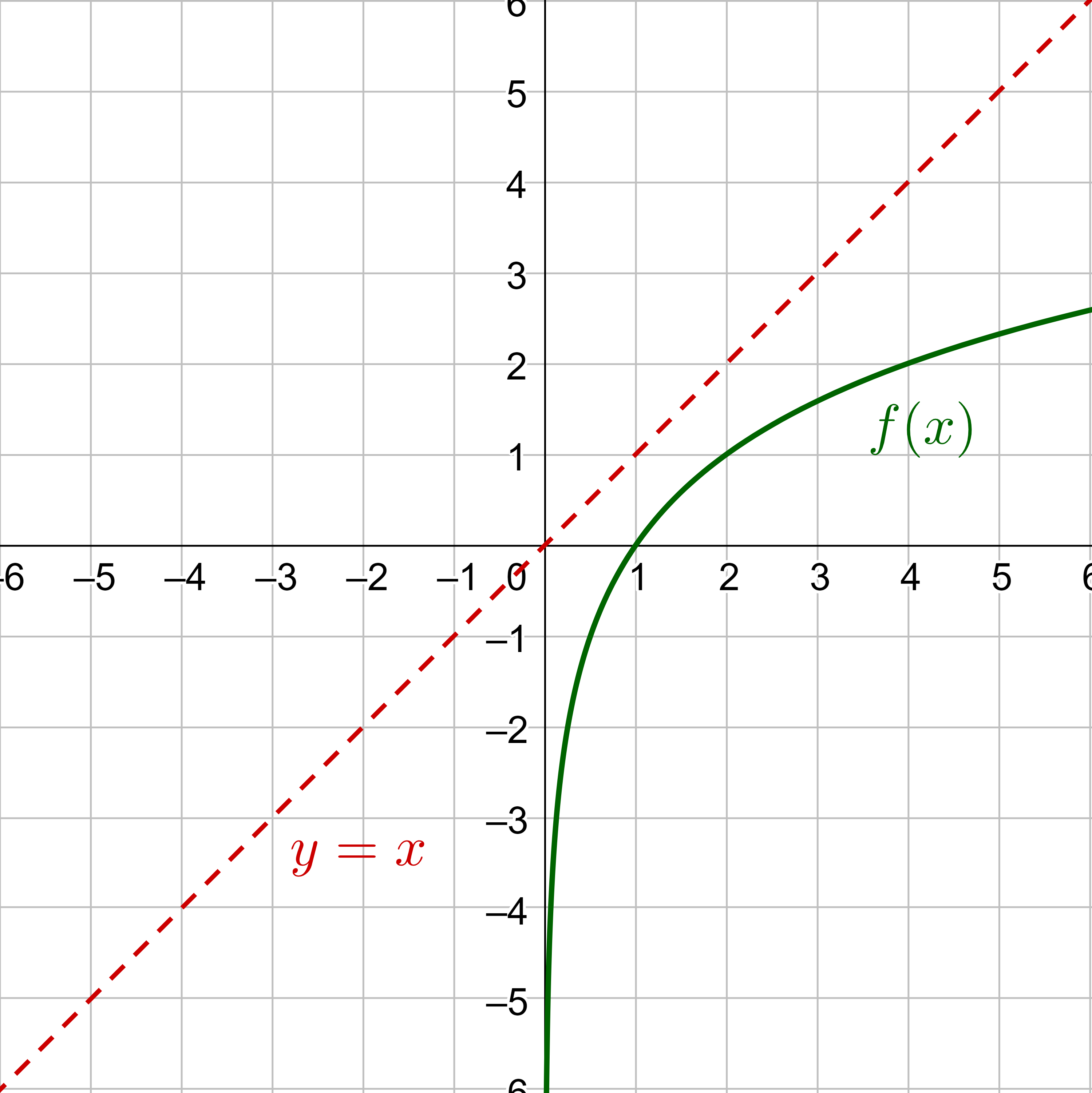
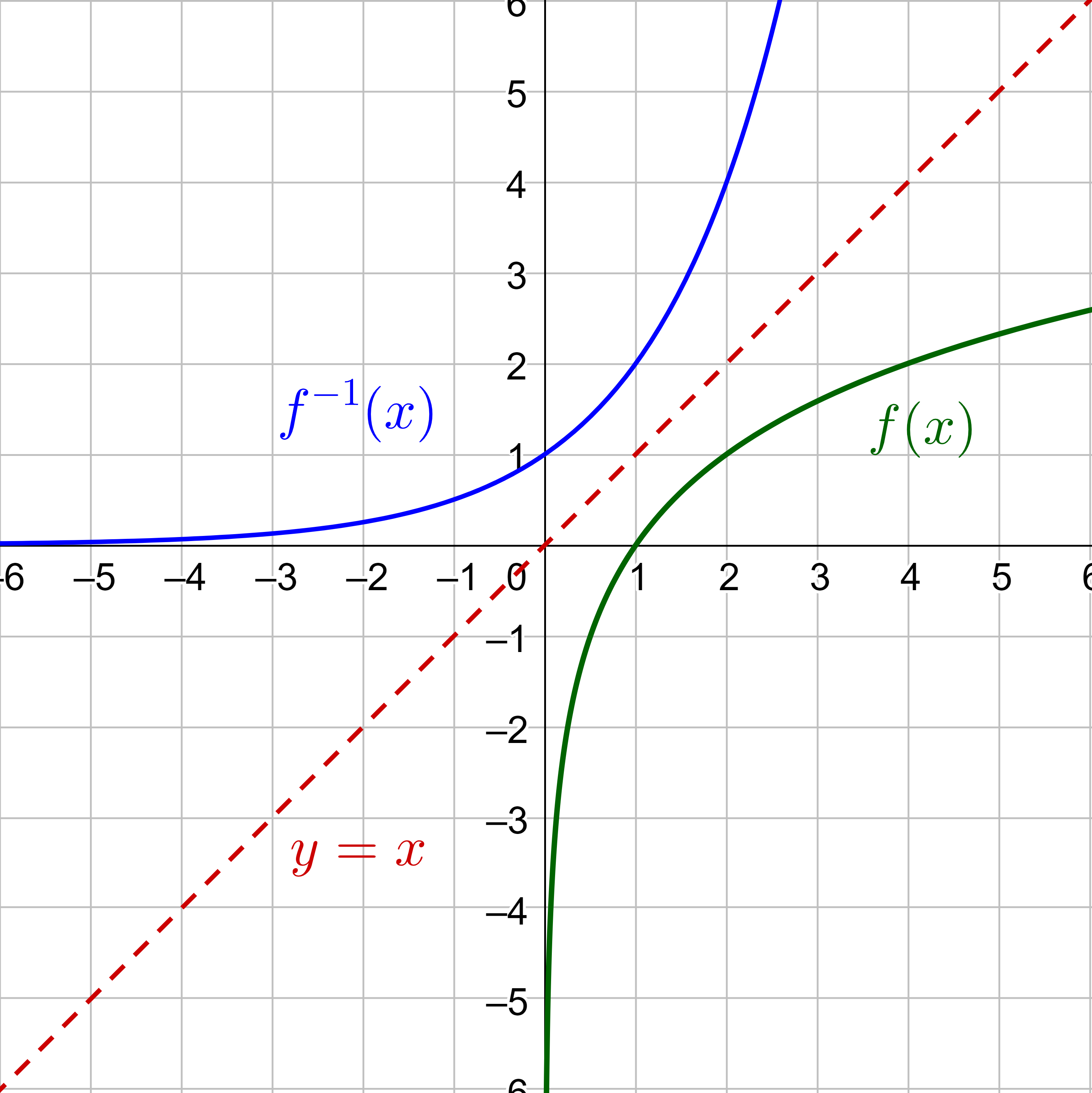
Solution
The inverse graph is a reflection over the line y = x, so find a lot of points and move them the same distance onto the other side of the line.
OR the inverse switches the x and y-coordinates. So, take a bunch of points of f(x) and switch their coordinates as in Table 1. Then graph the new points.
| Point on f(x) | Point on f−1(x) |
|---|---|
| (4, 2) → | (2, 4) |
| (2, 1) → | (1, 2) |
| (1, 0) → | (0, 1) |
| (1/2, −1) → | (−1, 1/2) |
| (1/4, −2) → | (−2, 1/4) |
If f(x) is in the graph below, sketch a graph of f−1(x).
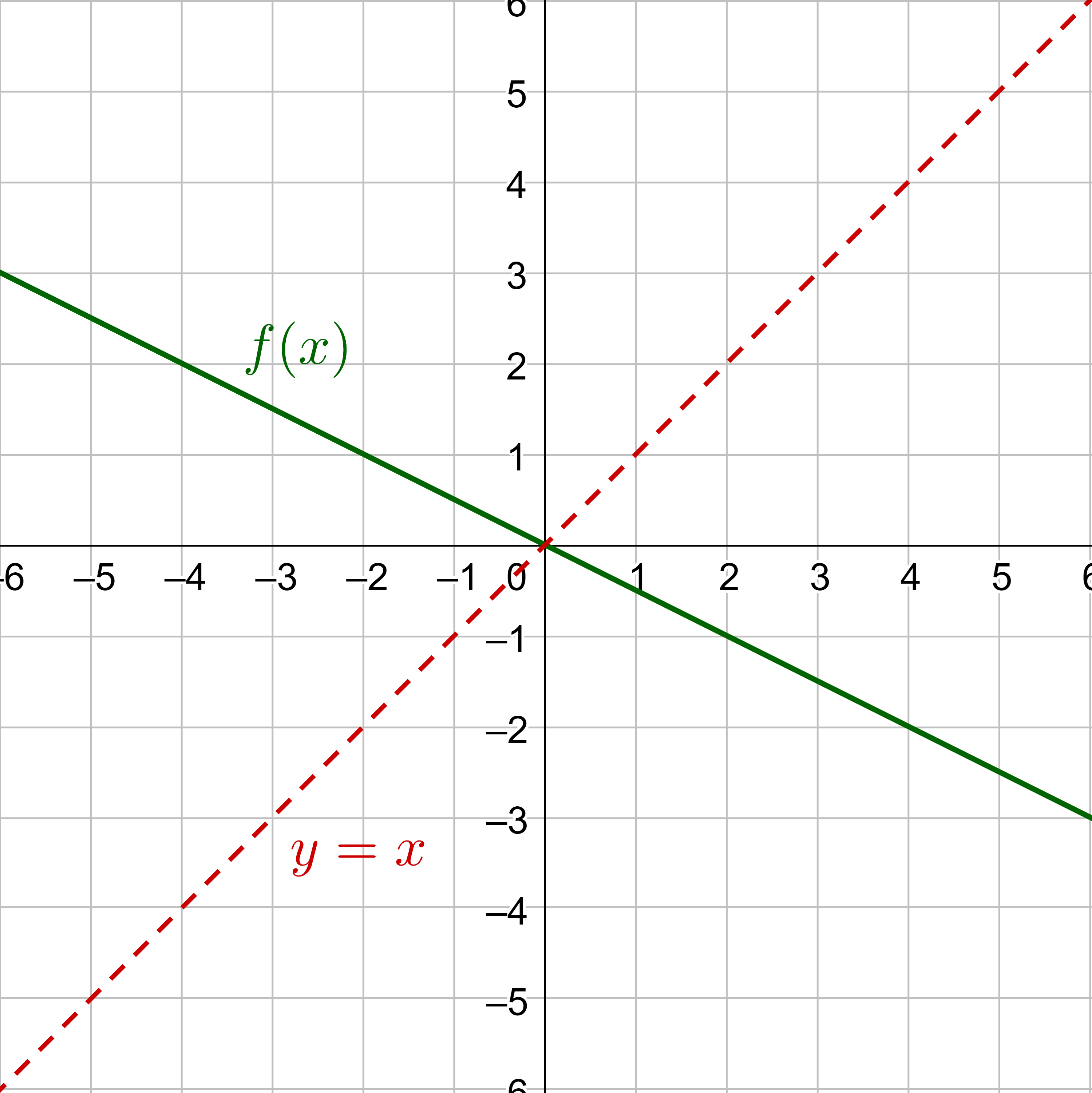
Solution
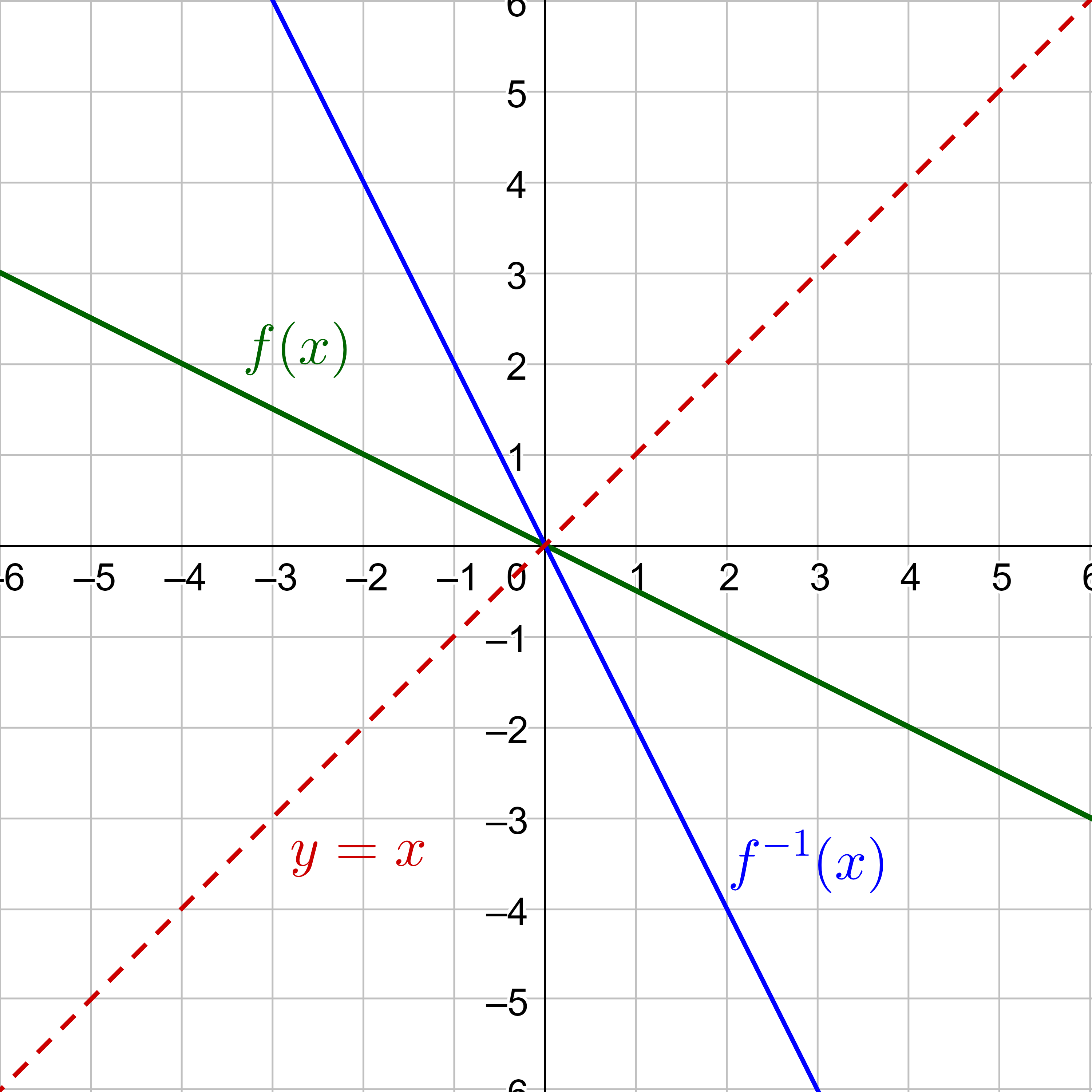
f(x) and g(x) are inverses if either f(g(x)) = x or g(f(x)) = x.
If either statement is true, then both are true, and g = f−1 and f = g−1. If either statement is false, then both are false.
The range of a function f(x) is the domain of the inverse function f−1(x).
The domain of f(x) is the range of f−1(x).
If the domain of the original function needs to be restricted to make it one-to-one, then this restricted domain becomes the range of the inverse function.
The graph of an inverse is the reflection of f(x) over the line y = x.
To find the inverse graph
OR
Helpful videos about this lesson.