Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Come to me, all you who are weary and burdened, and I will give you rest. Matthew‬ ‭11‬:‭28‬ ‭NIV‬‬

3-01 Exponential Functions

Mr. Wright teaches the lesson.

Summary: In this section, you will:

Evaluate exponential functions with base b.
Graph exponential functions with base b.
Evaluate and graph exponential functions with base e.

SDA NAD Content Standards (2018): PC.4.1, PC.5.3

Credit cards — Figure 1: credit (Picserver/Nick Youngson)

Credit card companies charge interest every day. Banks pay interest every month. How much money would be owed after several years? Or how much money is in a bank account after 10 years? These questions can be answered using exponential functions.

Evaluate Exponential Functions

Repeated addition is multiplication. For example, 4 + 4 + 4 + 4 + 4 = 5(4). Repeated multiplication is exponents. For example, 4 ⋅ 4 ⋅ 4 ⋅ 4 ⋅ 4 = 4⁵. An exponential function is a function that has the variable in the exponent.

Exponential Functions

An exponential function is in the form of

f(x) = ab^x

where b > 0, b ≠ 1, and x is a real number.

Example 1: Evaluate Exponential Functions

Use a calculator to evaluate the following functions.

f(x) = 2^x; x = 3
g(x) = 5(3)^{x + 1}; x = 3
h(x) = 6^−x; x = −2

Solution

f(3) = 2³ In a calculator type 2 ^ 3 ENTER. The display reads 8.
g(3) = 5(3)^{3 + 1} In a calculator type 5 ( 3 ) ^ ( 3 + 1 ) ENTER. The display reads 405.
h(−2) = 6⁻⁽⁻²⁾ In a calculator type 6 ^ (-) ( (-) 2 ) ENTER. The display reads 36.

Try It 1

Evaluate f(x) = 2 $(\frac{1}{2})$ ^{x − 1} when x = 5

Answer

1⁄8 = 0.125

Graph Exponential Functions

The graphs of exponential functions have a characteristic ever-changing curve as in figure 2.

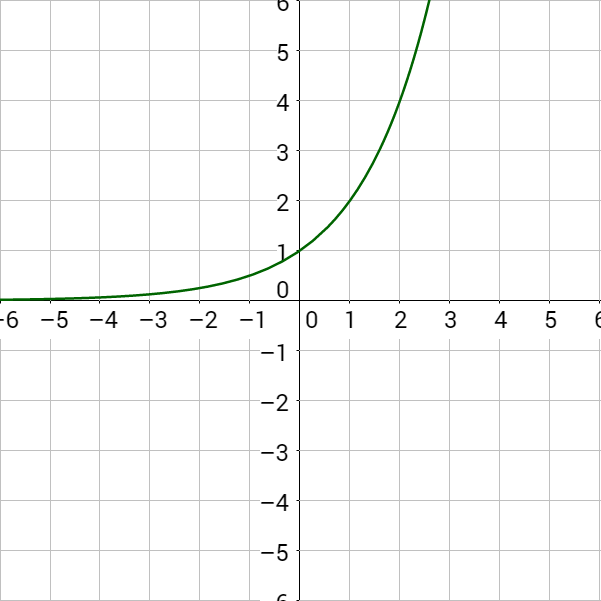
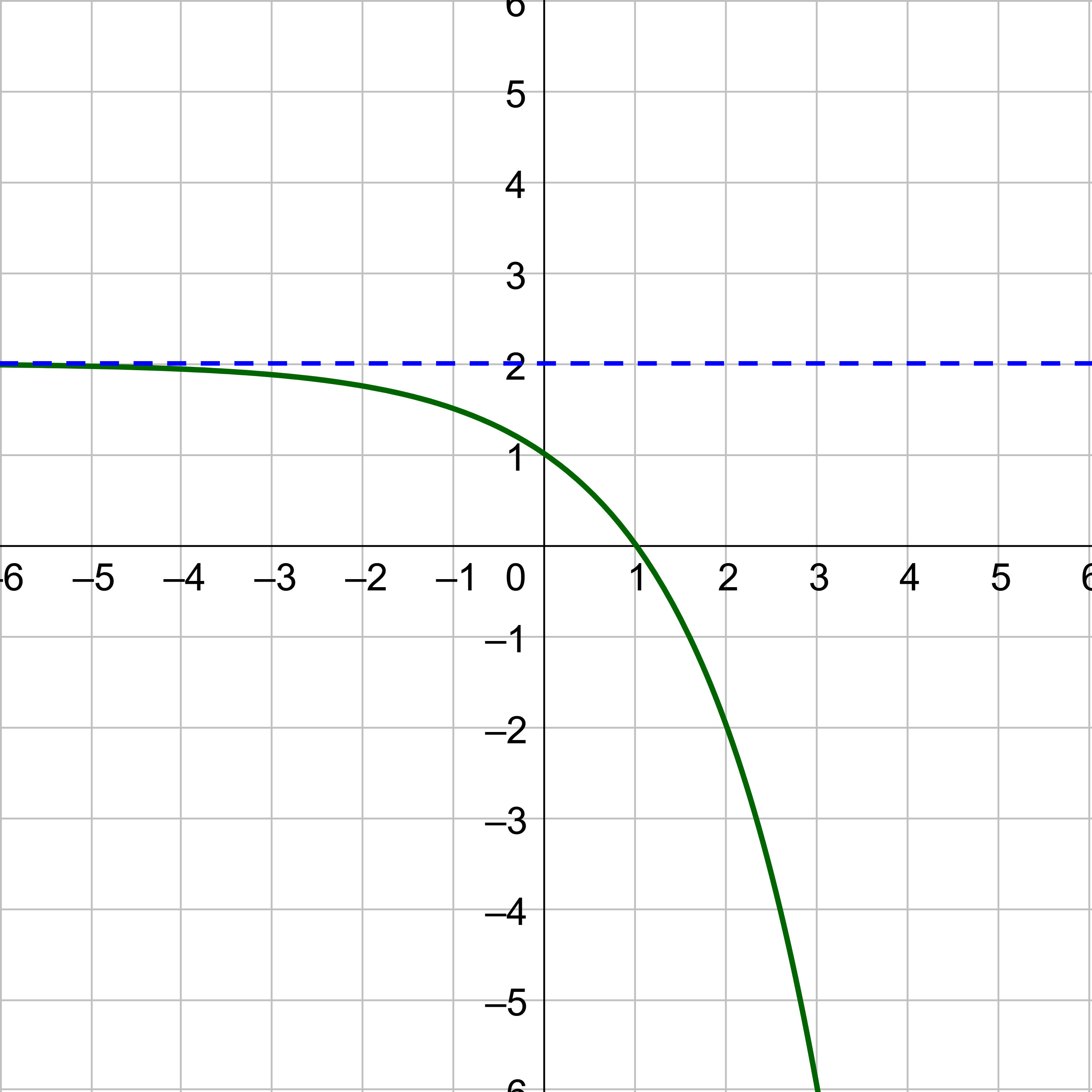
Notice the domain is all real numbers because any real number can be an exponent. The range is y > 0 if a > 0; and y < 0 if a < 0. The y-intercept is (0, a), and horizontal asymptote is y = 0.

Properties of Exponential Graphs

For f(x) = ab^x, then

Domain is all real numbers.
Range is y > 0 if a > 0.
Range is y < 0 if a < 0.
y-intercept is (0, a).
Horizontal asymptote is y = 0.
If b > 1, then the function is exponential growth.
If b < 1, then the function is exponential decay.

How to Graph an Exponential Function

Create a table of values by choosing inputs and calculating outputs.
Plot the points.
Draw a curve through the points.
Verify that the domain, range, y-intercepts, and horizontal asymptote of the graph match the function.

Example 2: Graph an Exponential Function

Graph

f(x) = 3^x
g(x) = 5^x

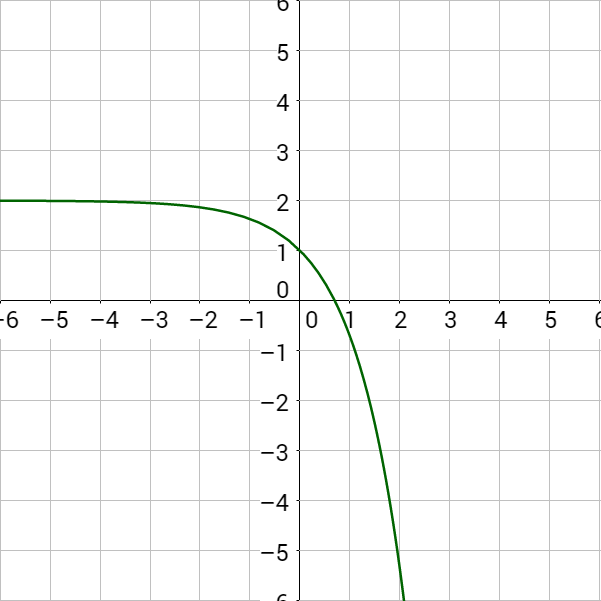
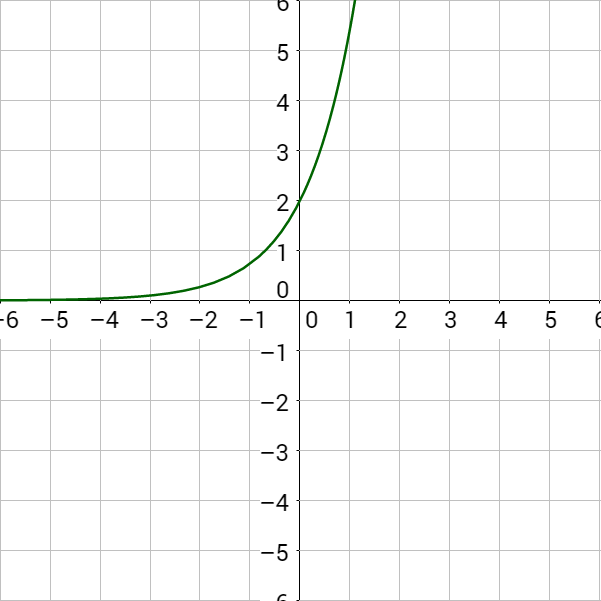
Are these exponential growth or decay?

Solution

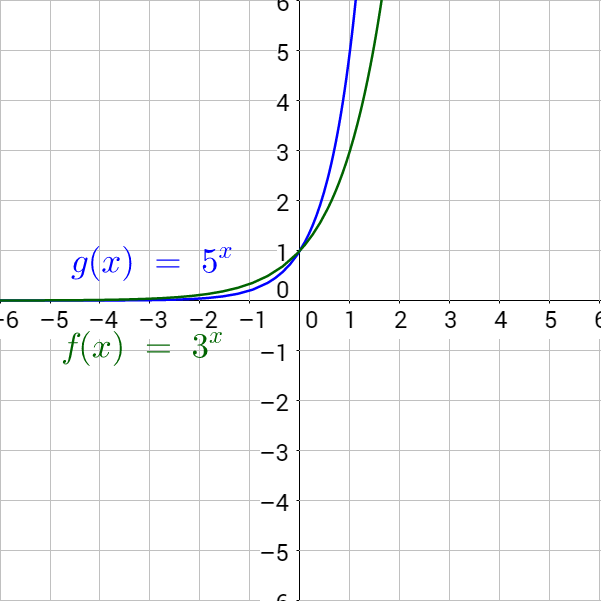
f(x)=3^x and g(x)=5^x — Figure 3 f(x) = 3^x (brown) and g(x) = 5^x (blue)

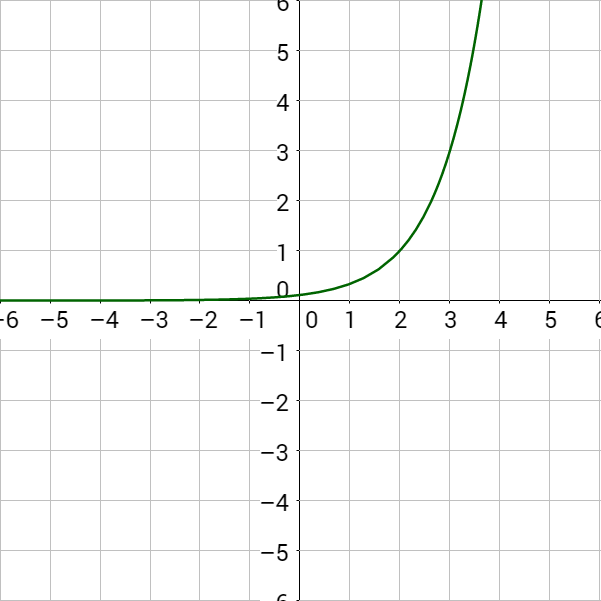
Since b > 0 in both cases, this is exponential growth. Notice the graph increases.

Example 3: Graph an Exponential Function

Graph

$f (x) = {(\frac{1}{3})}^{x}$
$g (x) = {(\frac{1}{5})}^{x}$

Are these exponential growth or decay?

Solution

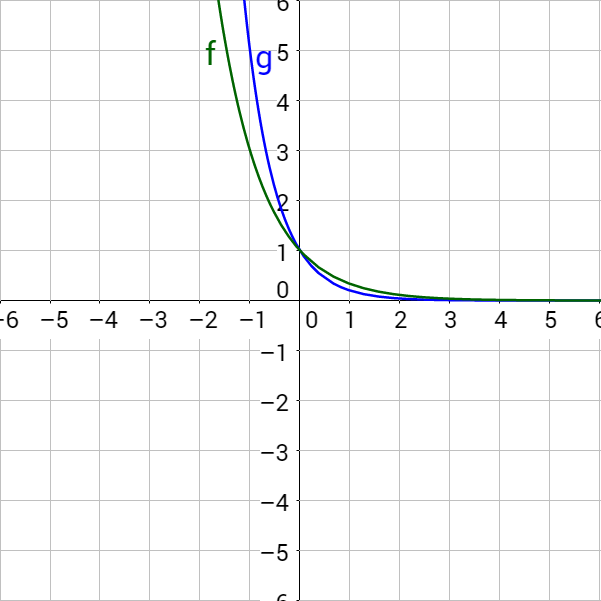
f(x)=(1/3)^x and g(x)=(1/5)^x — Figure 4 $f (x) = {(\frac{1}{3})}^{x}$ (brown) and $g (x) = {(\frac{1}{5})}^{x}$ (blue)

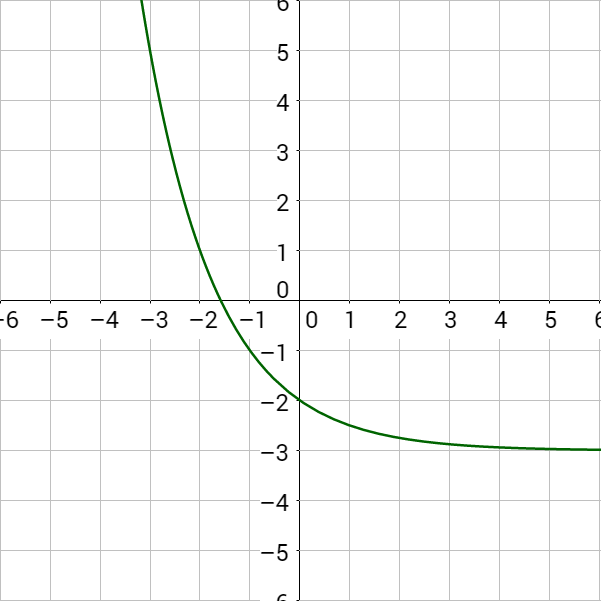
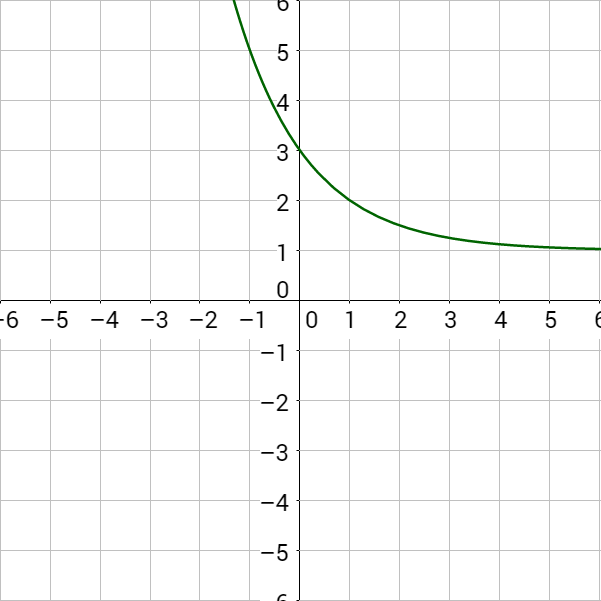
Since b < 0 in both cases, this is exponential decay. Notice the graph decreases.

Try It 2

Graph $h (x) = (\frac{1}{2}) 3^{x}$

Answer

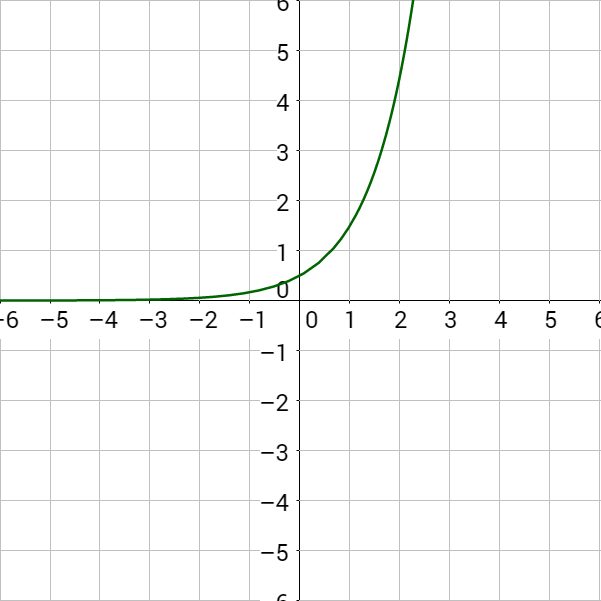
Notice the graphs of exponential growth functions like those in Example 2 always increase. The graphs of exponential decay functions like those in Example 3 always decrease. Because the graphs never switch from increasing to decreasing or vise versa, each input corresponds to a unique output. This type of function is called one-to-one. Each x gives a unique y-value that is not paired with another x.

Exponential functions follow the rules of transformations as given in Lesson 1-07.

Example 4: Transformations of Exponential Graphs

Describe the transformation and graph the following functions.

g(x) = 3(2)^{x − 1}
$h (x) = - {(\frac{2}{3})}^{x + 2} + 1$

Solution

Vertical shift by factor of 3, shift right 1

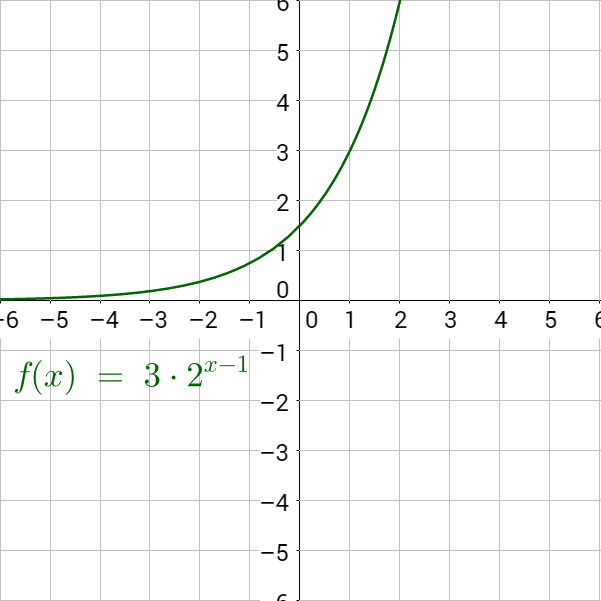
Figure 5 g(x) = 3(2)^{x − 1}
Reflected over the x-axis, shifted left 2 and up 1

Figure 6 $h (x) = - {(\frac{2}{3})}^{x + 2} + 1$

Try It 3

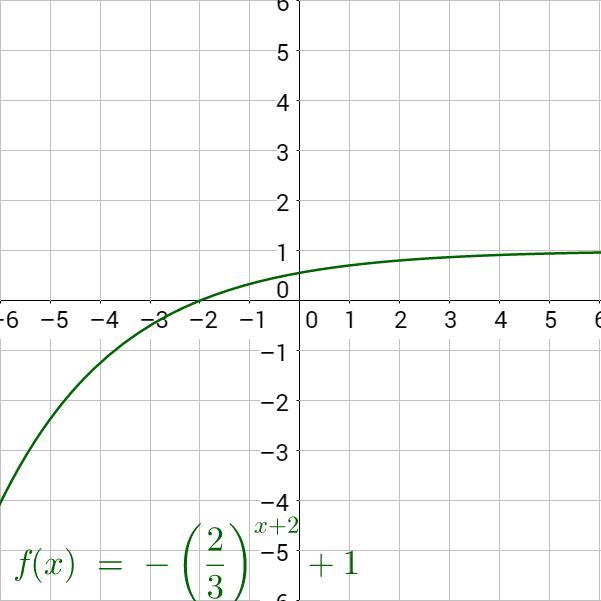
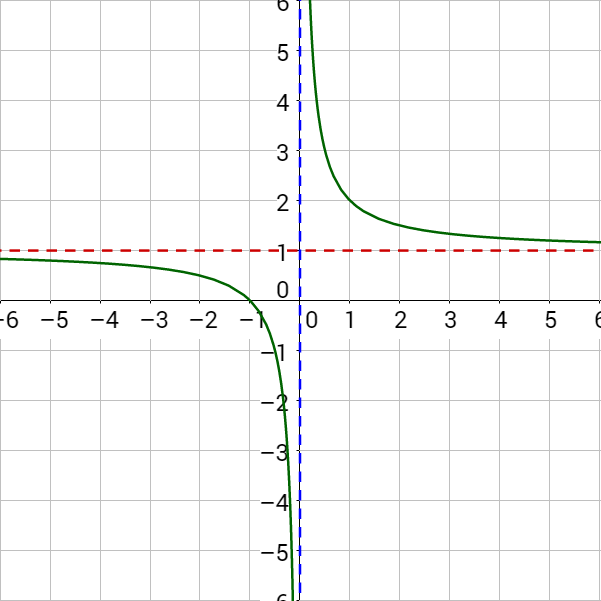
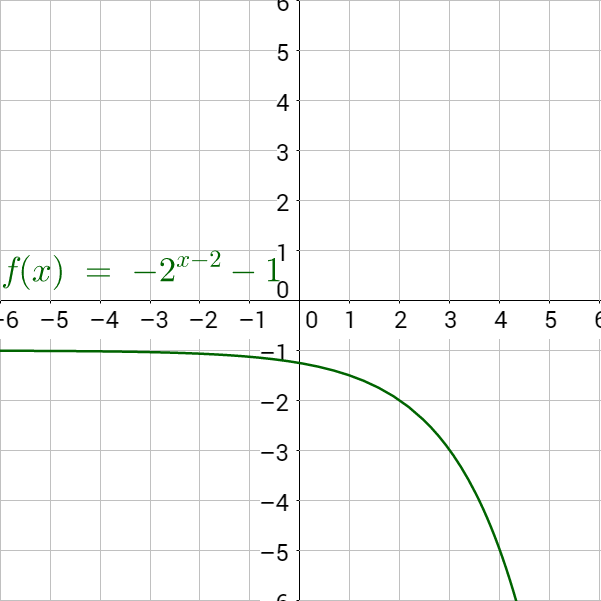
Describe the transformation and graph the following function: f(x) = −(2)^{x − 2} − 1.

Answer

Reflected over the x-axis, shifted right 2 and down 1.

The Natural Base e

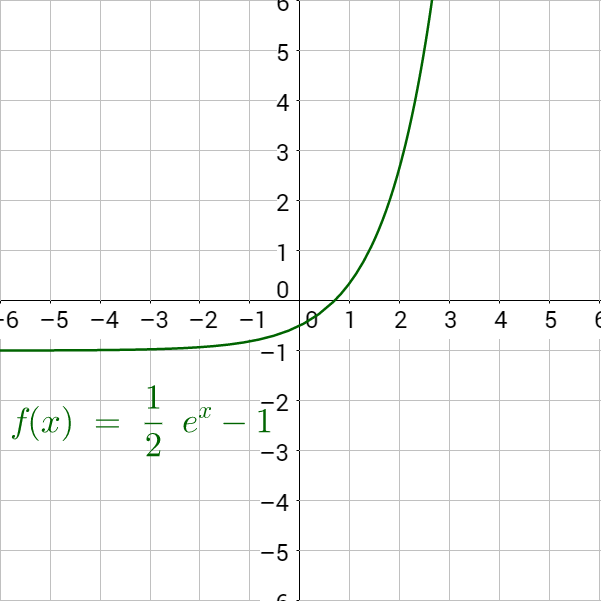
Many uses of exponential functions are simplest using the number e ≈ 2.718281828…. This number is called the natural base and is found by letting n get very large and approach ∞ in the expression ${(1 + \frac{1}{n})}^{n}$ . The natural base, e, can be useful in calculus because the slope of the function f(x) = e^x is also e^x. For example, the slope of the graph of f(x) = e^x at x = 2 is e².

Example 5: Evaluate Exponential Functions with Base e

Use a calculator to evaluate the following functions.

f(x) = e^x; x = 3
g(x) = 5(e)^{x + 1}; x = 3
h(x) = e^−x; x = −2

Solution

f(3) = e³ In a calculator type e^x 3 ENTER. The display reads 20.086.
g(3) = 5(e)^{3 + 1} In a calculator type 5 e^x ( 3 + 1 ) ENTER. The display reads 272.991.
h(−2) = e⁻⁽⁻²⁾ In a calculator type e^x (-) ( (-) 2 ) ENTER. The display reads 7.389.

Try It 4

Evaluate j(x) = 2e^{x + 1} when x = −3.

Answer

0.736

Example 6: Graph an Exponential Function with Base e

Graph $f (x) = \frac{1}{2} e^{x} - 1$ .

Solution

f(x)=(1/2)e^x-1 — Figure 7 $f (x) = \frac{1}{2} e^{x} - 1$

Applications

When a credit card company or bank calculates, or compounds, interest, they quote a yearly interest rate. But the banks then calculate interest monthly or daily. To derive a formula for calculating compound interest, look at the pattern. In the following table P is the principle and r is the yearly interest rate (APR). Each year's interest is calculated by Pr. The amount in the account will be P + Pr which is the principle plus the interest. This factors to P(1 + r).

Year	Balance
0	P₀ = P
1	P₁ = P₀(1 + r) = P(1 + r)
2	P₂ = P₁(1 + r) = P(1 + r)(1 + r) = P(1 + r)²
3	P₃ = P₂(1 + r) = P(1 + r)²(1 + r) = P(1 + r)³
t	P_t = P(1 + r)^t

If the interest is compounded n times per year, the formula needs to be modified to $A = P {(1 + \frac{r}{n})}^{n t}$ .

Now think about what happens as the number of compoundings per year gets very large. The most often interest can be compounded is continuously where the interest is calculated every instant when n = ∞. To derive the formula for continuously compounded interest, let m = ⁿ⁄_r, so n = mr.

$\begin{matrix} A = P {(1 + \frac{r}{m r})}^{m r t} \\ A = P {(1 + \frac{1}{m})}^{m r t} \\ A = P {({(1 + \frac{1}{m})}^{m})}^{r t} \end{matrix}$

For continuous compounding, m becomes large and approaches ∞. The expression in parentheses is the definition of e when m approaches ∞.

A = Pe^rt

Compound Interest

$A = P {(1 + \frac{r}{n})}^{n t}$

where A is the current amount, P is the principle or initial amount, r is the interest rate as a decimal, n is the number of compoundings per year, and t is the time in years.

Continuously Compounded Interest

A = Pe^rt

Example 7: Compound Interest

A high school student deposits $1000 in a mutual fund that averages 8% APR interest. How much is the mutual fund worth after 10 years if the interest is compounded

monthly?
daily?
continuously?

Which scenario gives the most money?

Solution

P = $1000 because that is the initial amount of money. r = 0.08 or 8%, and t = 10 yrs.

$A = 1000 {(1 + \frac{0.08}{n})}^{n (10)}$

There are 12 months in a year, so n = 12. $A = 1000 {(1 + \frac{0.08}{12})}^{12 (10)} = $2219.64$
There are 365.25 days in a year, so n = 365.25. $A = 1000 {(1 + \frac{0.08}{365.25})}^{365.25 (10)} = $2225.35$
Compounding continuously uses the other function. A = 1000e^0.08(10) = $2225.54

Compounding continuously produces the most money. The higher the value of n, the more money there is in the account. That is why banks pay interest monthly, but charge interest on credit cards daily.

Try It 5

A college student goes on a weekend shopping spree and charges $500 on a credit card that charges 25% APR interest compounded daily. If they don't pay anything, how much will they owe after 1 year?

Answer

$641.96 plus late payment fees

Lesson Summary

Exponential Functions

An exponential function is in the form of

f(x) = ab^x

where b > 0, b ≠ 1, and x is a real number.

Properties of Exponential Graphs

For f(x) = ab^x, then

Domain is all real numbers.
Range is y > 0 if a > 0.
Range is y < 0 if a < 0.
y-intercept is (0, a).
Horizontal asymptote is y = 0.
If b > 1, then the function is exponential growth.
If b < 1, then the function is exponential decay.

How to Graph an Exponential Function

Create a table of values by choosing inputs and calculating outputs.
Plot the points.
Draw a curve through the points.
Verify that the domain, range, y-intercepts, and horizontal asymptote of the graph match the function.

Compound Interest

$A = P\left(1+\frac{r}{n}\right)^{nt}$

where A is the current amount, P is the principle or initial amount, r is the interest rate as a decimal, n is the number of compoundings per year, and t is the time in years.

Continuously Compounded Interest

A = Pe^rt

Helpful videos about this lesson.

Practice Exercises

Two types of fish have been introduced into a pond. The population of fish A can be modeled by A(t) = 20(1.05)^t and fish B by B(t) = 40(1.025)^t where t is in years. (Round your answers to the nearest whole number.)

Which fish population is growing at a faster rate?
What type of fish was initially introduced in greater quantity?
Assuming the models are still accurate, which type of fish will have the bigger population after 10 years?

Evaluate the function for the given values.

f(x) = 2⋅3^x
1. f(0)
2. f(2)
3. f(−1)
4. f(1⁄2)
f(x) = −e^{x + 1}
1. f(0)
2. f(2)
3. f(−1)
4. f(1⁄2)
What is an asymptote?
The graph of f(x) = 2^x is reflected over the x-axis and stretched vertically by a factor of 5. (a) Write the new function g(x), and (b) State its y-intercept, domain, and range.

Write a function that represents the transformation of f(x) = 3^x.

Shift f(x) 3 units right and 2 units down
Reflect f(x) over the y-axis and shift 2 units up

The graph is a transformation of y = 2^x. Write an equation describing the transformation.

Graph the function. Then state the domain, range, asymptote, and whether it is exponential growth, decay, or neither.

f(x) = 3^{x − 2}
$g (x) = {(\frac{1}{2})}^{x} - 3$
h(x) = 2^{1 − x} + 1
j(x) = −e^x + 2
k(x) = 2e^x
Sally invests $1500 in an account that pays 7.5% interest. How much is the account worth after 20 years if the interest is compounded
1. annually?
2. semiannually?
3. monthly?
4. daily?
5. continuously?

Mixed Review

(2-09) Solve $\frac{x + 1}{x} \leq 0$ .
(2-08) Find the asymptotes and graph $f (x) = \frac{x + 1}{x}$ .
(2-05) Find the rational zeros of x⁴ − 2x³ − 11x² + 6x + 24.
(2-06) Find the irrational zeros of x⁴ − 2x³ − 11x² + 6x + 24.
(1-09) Verify that f(x) = 2x + 3 and $g (x) = \frac{x - 3}{2}$ are inverses by finding their composition.

Answers

Fish A has a larger base (1.05).
Fish B had 20 more than fish A.
Fish A will have 33 fish and B will have 51 fish.
2; 18; 2⁄3; $2 \sqrt{3}$
−2.718; −20.086; −1; −4.482
An asymptote is a line that the graph of a function approaches, as x either increases or decreases without bound or approaches from the left or right. The horizontal asymptote of an exponential function tells us the limit of the function’s values as the independent variable gets either extremely large or extremely small.
g(x) = −5(2)^x; y-int: (0, −5); domain: all real numbers; range: (−∞, 0)
g(x) = 3^{x − 3} − 2
g(x) = 3^−x + 2
y = −2^x + 2
; domain: all real numbers; range: (0, ∞); y = 0; growth
; domain: all real numbers; range: (−3, ∞); y = −3; decay
; domain: all real numbers; range: (1, ∞); y = 1; decay
; domain: all real numbers; range: (−∞, 2); y = 2; neither
; domain: all real numbers; range: (0, ∞); y = 0; growth
$6371.78; $6540.57; $6691.23; $6721.50; $6722.53
[−1, 0)
VA: x = 0; HA: y = 1;
−2, 4
$\pm \sqrt{3}$
f(g(x)) = x