Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Why do you look for the living among the dead? He is not here; he has risen! Luke 24:5-6 NIV

3-03 Properties of Logarithms

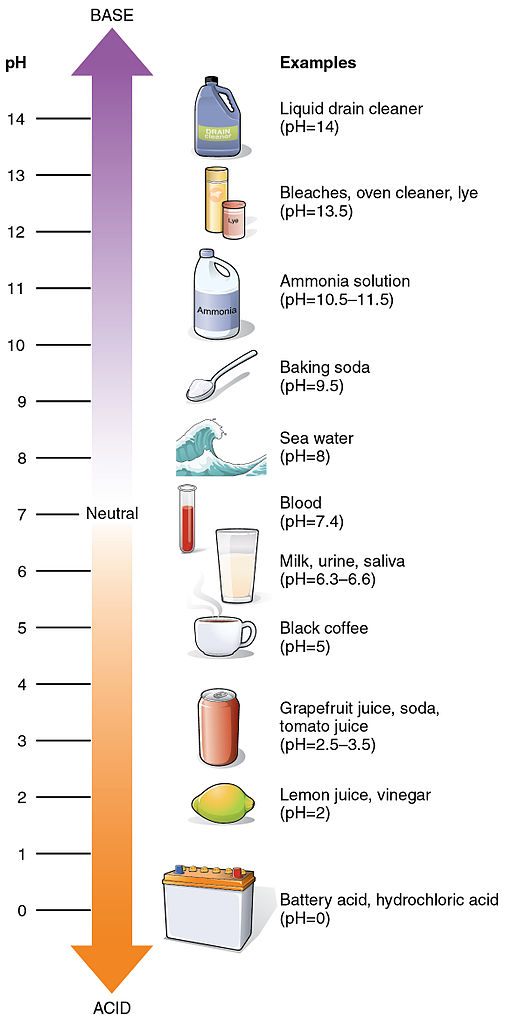
In chemistry, pH is used as a measure of the acidity or alkalinity of a substance. The pH scale runs from 0 to 14. Substances with a pH less than 7 are considered acidic, and substances with a pH greater than 7 are said to be alkaline. Our bodies, for instance, must maintain a pH close to 7.35 in order for enzymes to work properly. To get a feel for what is acidic and what is alkaline, consider the following pH levels of some common substances:

• Battery acid: 0.8
• Stomach acid: 2.7
• Orange juice: 3.3
• Pure water: 7 (at 25° C)
• Human blood: 7.35
• Fresh coconut: 7.8
• Sodium hydroxide (lye): 14

To determine whether a solution is acidic or alkaline, we find its pH, which is a measure of the number of active positive hydrogen ions in the solution. The pH is defined by the following formula, where H⁺ is the concentration of hydrogen ion in the solution in mol/L.

pH = −log([H⁺])
$$=log\left(\frac{1}{\left[H^{+}\right]}\right)$$

The equivalence of −log([H⁺]) and $log\left(\frac{1}{\left[H^{+}\right]}\right)$ is one of the logarithm properties examined in this section.

Properties of Logarithms

Remember that logarithms equal exponents. When two exponential expressions with the same base are multiplied, then the exponents are added. So when a logarithm is taken of two multiplied values, it can be rewritten as the sum of two separate logarithms. This is the product property.

log_b (uv) = log_b u + log_b v

A similar property is the quotient property. When exponential expressions are divided, then the exponents are subtracted. So when a logarithm is taken of two divided values, it can be rewritten as the difference of two separate logarithms.

$${log}_b\left(\frac{u}{v}\right)={log}_{b}u-{log}_{b}v$$

When an exponential expression is given an additional exponent, the exponents are multiplied. The power property says that an exponent on a logarithm, it can be rewritten as multiplication.

log_b uⁿ = n log_b u

Expand and Condense Logarithmic Expressions

Separating expressions into several separate logarithmic expressions or combining logarithmic expressions together can be useful for solving logarithmic equations. Expanding expressions means to rewrite a single logarithmic expression into several expressions. Condensing means to do the opposite and rewrite several logarithmic expressions into a single logarithm.

Change-of-Base Formula

There is a reason why most calculators only have the common log and natural log buttons. The reason is that the base of the logarithm can be changed with a formula.

To derive the formula, call the logarithm we are trying to evaluate y.

log_b x = y

Rewrite it as an exponential function.

x = b^y

Remember the Golden Rule of Algebra, what you do to one side of the equation, do to the other side. Take a logarithm of both sides. Any base is fine.

log_c x = log_c b^y

Use the power property on the right hand side, then solve for y.

log_c x = y log_c b
$$\frac{{log}_{c}x}{{log}_{c}b}=y$$

Replace y with the logarithm that it equals from the first step which results in the change-of-base formula.

$${log}_{b}x=\frac{{log}_{c}x}{{log}_{c}b}$$

Graph Logarithmic Functions

Since logarithms are inverses of exponential functions, the graph of a logarithm is a reflection of an exponential function reflected over the line y = x.

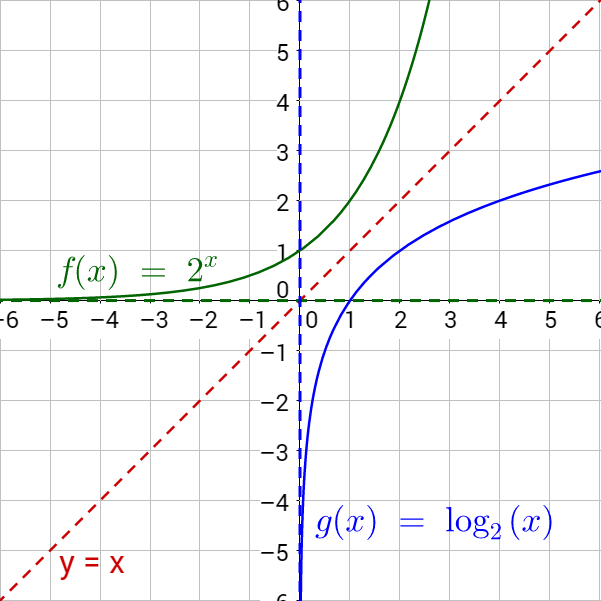
The graph of a logarithmic function, g(x) = log_b (x − h) + k has several properties:

• Vertical asymptote at x = h
• x-intercept at (1, 0) if h = k = 0
• Domain: (h, ∞)
• Range: All Real Numbers
• Increasing from h to ∞

Logarithmic functions can be easily graphed by using the change-of-base formula to create a table of values. It is also important to graph the vertical asymptote.

Graph a Logarithmic Function

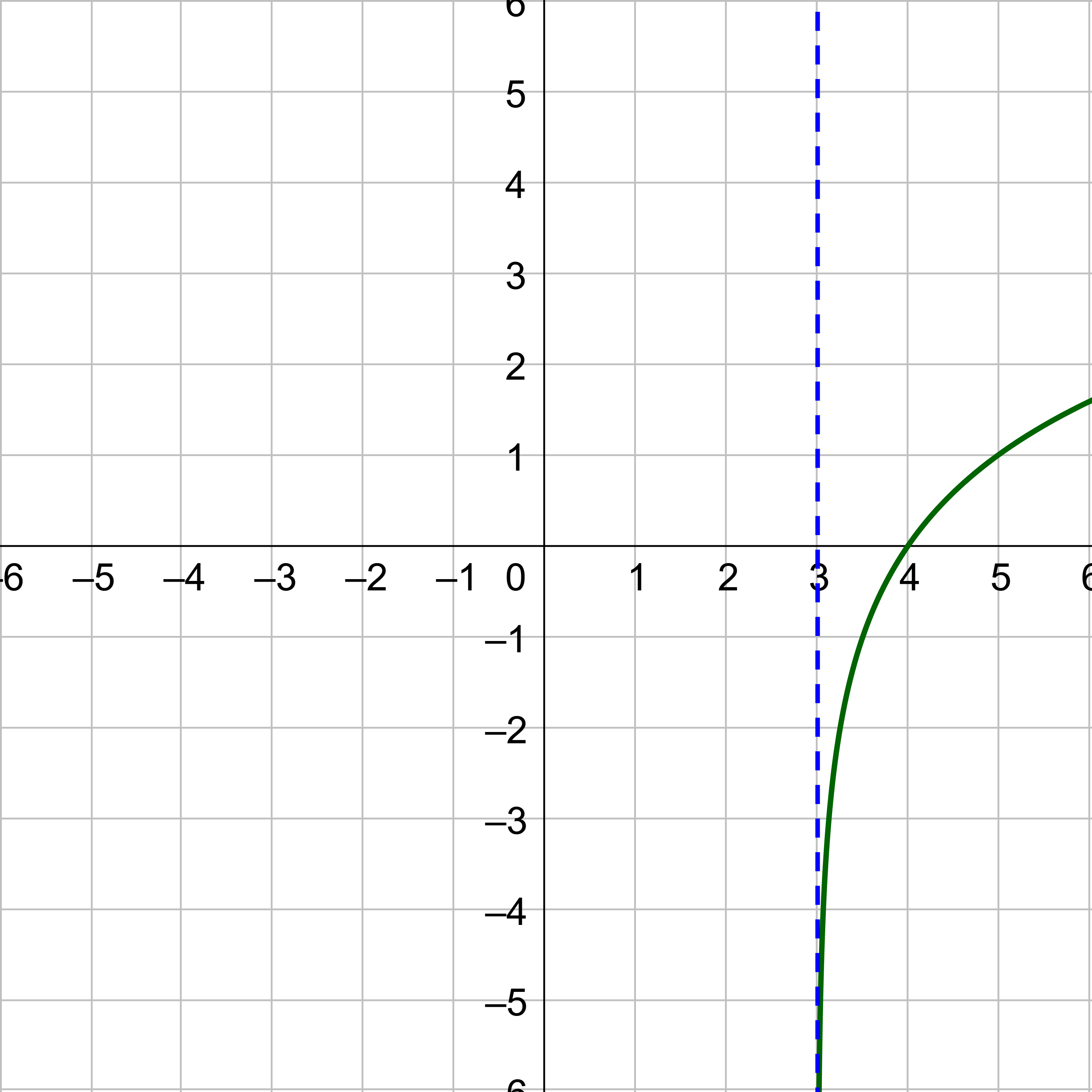
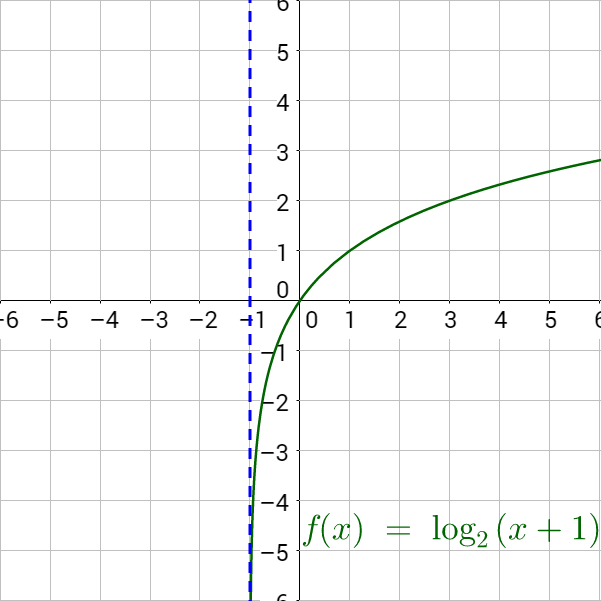
Graph f(x) = log₂ (x + 1).

Solution

Compare f(x) with g(x) = log_b (x − h) + k. This gives h = −1, so the vertical asymptote is x = −1.

Use the change-of-base formula to rewrite the function with a base on the calculator.

$$\begin{array}{l}f\left(x\right)={log}_2\left(x+1\right)\\ =\frac{{log}_{10}\left(x+1\right)}{{log}_{10}2}\\ =\frac{log\left(x+1\right)}{log2}\end{array}$$

Create a table of values using x-values larger than h because that is the domain.

x	0	1	2	3	4	5	6
f(x)	0	1	1.585	2	2.322	2.585	2.807

When drawing the graph, graph the asymptote and make sure the curve approaches the asymptote.

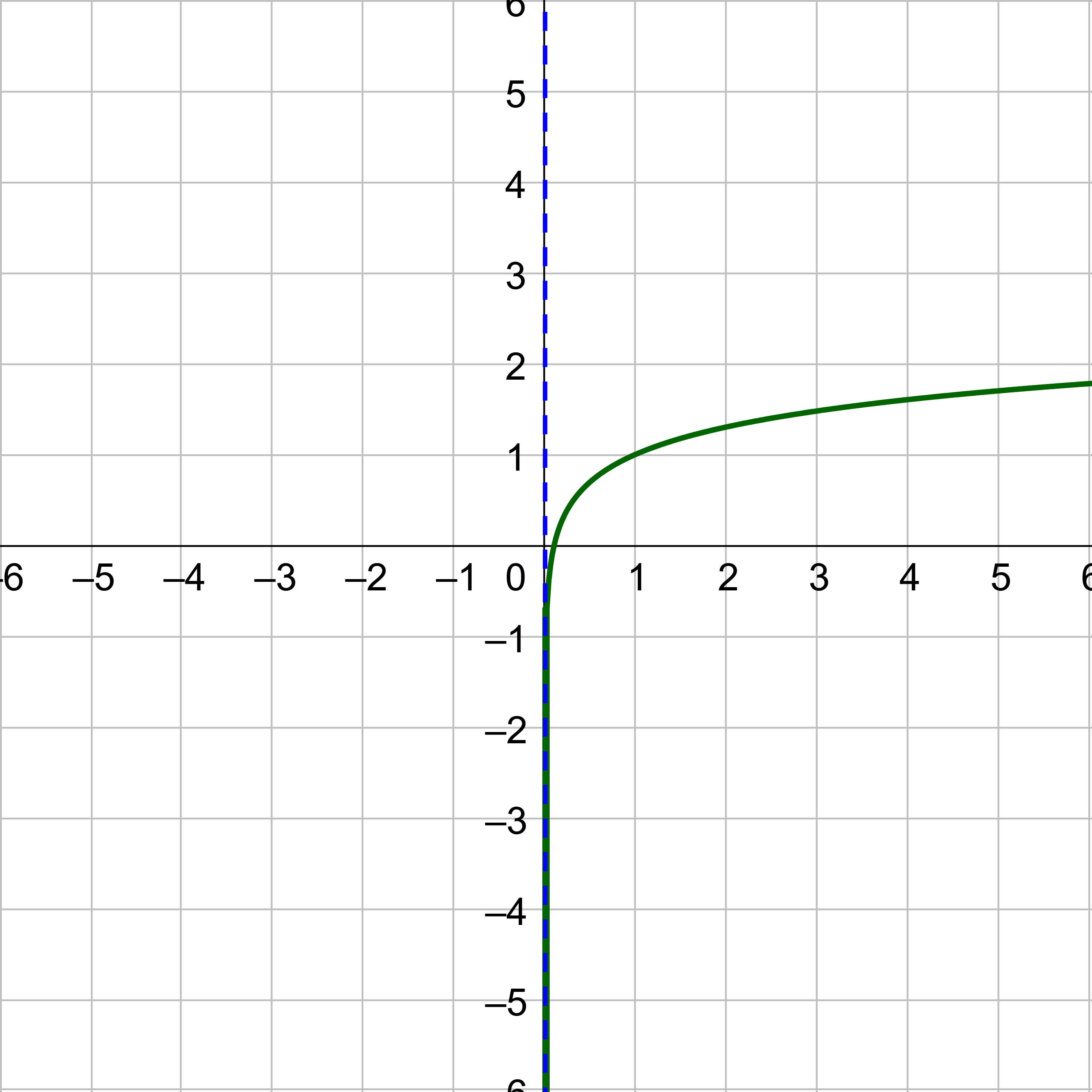
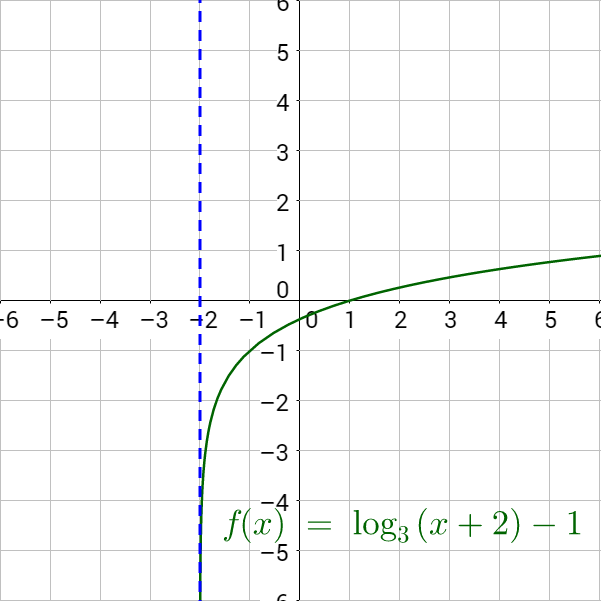
Graph g(x) = log₃ (x + 2) − 1.

Answer

Practice Exercises

1. Which type of translation affect the domain of a logarithmic function?
2. Rewrite the expression in terms of log₃ 4 and log₃ 8.
3. log₃ 64
4. log₃ 2
5. Expand the following expressions.
6. log₃ (3xy⁴)
7. \(\log \left(\frac{m}{3n^3}\right)\)
8. \(\ln \left(\frac{2p^3}{e^t ·q}\right)\)
9. Condense the following expressions.
10. ln x + 2 ln y
11. 2 log₆ 3 + log₆ w − 4 log₆ t
12. log₂ 7 − 2 log₂ m − 4 log₂ n
13. Use the change-of-base formula to evaluate each expression as a quotient of natural logs. Use a calculator to approximate each to three decimal places.
14. log₇ 128
15. log_½ 7.3
16. State the asymptote, domain, and range. Then sketch the graph of the indicated function.
17. f(x) = log₂ (x − 3)
18. g(x) = log x + 1
19. h(x) = −2 ln (x − 3) + 1
20. Problem Solving
21. pH is a measure of active hydrogen ion in a solution. The formula pH = −log([H⁺]) is used to calculate pH where H⁺ is the hydrogen ion concentration in mol/L and pH is the pH level. What is the difference in pH level between battery acid with a hydrogen ion concentration of 1.58×10⁻¹ mol/L and orange juice with a hydrogen ion concentration of 5.01×10⁻⁴ mol/L?
22. Mixed Review
23. (3-02) Rewrite as an exponential equation: ln x = 7.
24. (3-02) Evaluate without using a calculator: log₃ (27) − 1.
25. (3-01) For the following exercises, graph the function. Then state the domain, range, asymptote, and whether it is exponential growth, decay, or neither: f(x) = ½e^x + 1
26. (2-09) Solve by graphing: 2x² − 5x − 3 ≤ 0.
27. (2-06) Solve x³ − 7x² + 17x − 15 = 0.

Answers

1. Shifting the function right or left will affect its domain.
2. 3 log₃ 4
3. log₃ 8 − log₃ 4
4. 1 + log₃ (x) + 4 log₃ (y)
5. log m − log 3 − 3 log n
6. ln 2 + 3 ln p − t − ln q
7. ln xy²
8. \(\log_{6} \left(\frac{9w}{t^4}\right)\)
9. \(\log_{2} \left(\frac{7}{m^2 n^4}\right)\)
10. 2.493
11. −2.868
12. VA: x = 3; Domain: (3, ∞); Range: (−∞, ∞);

    

13. VA: x = 0; Domain: (0, ∞); Range: (−∞, ∞);

    

14. VA: x = 3; Domain: (3, ∞); Range: (−∞, ∞);

    

15. 2.499
16. e⁷ = x
17. 2

18. 

    ; Domain: (−∞, ∞); Range: (1, ∞); HA: y = 1; Exponential growth
19. [−½, 3]
20. 3, 2 + i, 2 − i