Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Precalculus by Richard Wright
Are you not my student and
has this helped you?
This book is available
to download as an epub.
Therefore I tell you, do not worry about your life, what you will eat or drink; or about your body, what you will wear. Is not life more than food, and the body more than clothes? Look at the birds of the air; they do not sow or reap or store away in barns, and yet your heavenly Father feeds them. Are you not much more valuable than they? Can any one of you by worrying add a single hour to your life? Matthew 6:25-27 NIV
Summary: In this section, you will:
SDA NAD Content Standards (2018): PC.6.3
In John 6:1-15 and Matthew 1:13-21, the Bible tells the story of Jesus feeding the 5,000. Jesus went across the Sea of Galilee for some time with just his disciples, but the multitudes of people followed on land and quickly caught up with Him. So Jesus spent the day teaching and healing. Near evening, Jesus asked where to buy food for the 5,000 men plus women and children. The crowd has been estimated at 15,000 people. A boy had a lunch of five small barley loaves and two small fish. Jesus took the food, gave thanks, and broke the bread and fish. Then he passed out the pieces of bread and fish to the disciples to give to the people. If the bread and fish were each divided in half, how many time would it have to be divided to feed all 15,000 people?
This can be modeled by pieces = 7(2)t. If each person got one piece of food, the equation becomes 15,000 = 7(2)t. The lesson today is on how to solve these types of problems.
To solve any equation by graphing, follow the general procedure from last chapter.
Exponential functions have a one-to-one property which means each input, x, value gives one unique output, y, value. Each x gives only one y, and each y gives only one x. This means exponential equations have only one solution.
To solve an exponential equation using the one-to-one property.
Solve 3x + 2 = 27x.
Solution
Rewrite both sides of the equation as exponential functions with the same base. The right side is 27 which can be written as 33 using base 3 like the left side of the equation is.
3x + 2 = (33)x
3x + 2 = 33x
Since the bases are equal, then the exponents must also be equal. So rewrite an equation using the exponents. Then solve the equation.
x + 2 = 3x
2 = 2x
1 = x
Notice that when you check the answer by plugging in 1 for x, both sides equal 27. Thus 1 is a good solution.
Analysis
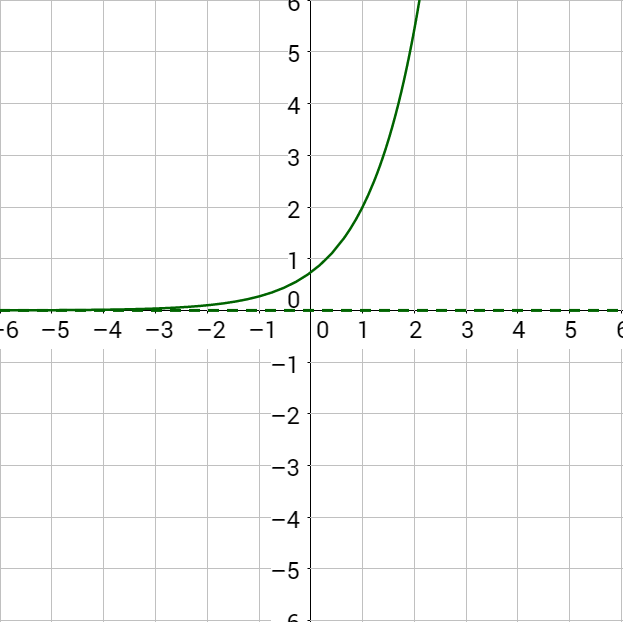
To solve this by graphing, subtract the 27x to make the right side 0.
3x + 2 − 27x = 0
Graph the left-hand side and find the x-intercept.
Since the x-intercept is (1, 0), the solution is x = 1.
Solve 4x − 1 = 16.
Answer
x = 3
Method 1 only works when both sides of the equation can easily be written as exponential expressions with the same base. If this cannot be done, more traditional methods of solving must be used. To solve any equation, inverses of the operations are used to get the variable alone. To undo multiplication, divide; to undo squaring, square root; to undo exponential, logarithm. So to solve an exponential equation use the inverse, a logarithm. This has the same effect as rewriting the exponential equation as a logarithm.
To solve an exponential equation using logarithms
Solve 5x + 2 = 17.
Solution
Notice the exponential expression, 5x + 2 is already isolated. So now take the log base 5 of both sides since the base of the exponential is 5.
5x + 2 = 17
log5 5x + 2 = log5 17
The properties of logarithms say that the log base 5 and the base 5 of the exponential cancel because they are inverses.
log5 5x + 2 = log5 17
x + 2 = log5 17
x = (log5 17) − 2
x ≈ −0.240
Plug −0.240 into the original equation and see that both sides approximate 17, so it is the correct solution.
Analysis
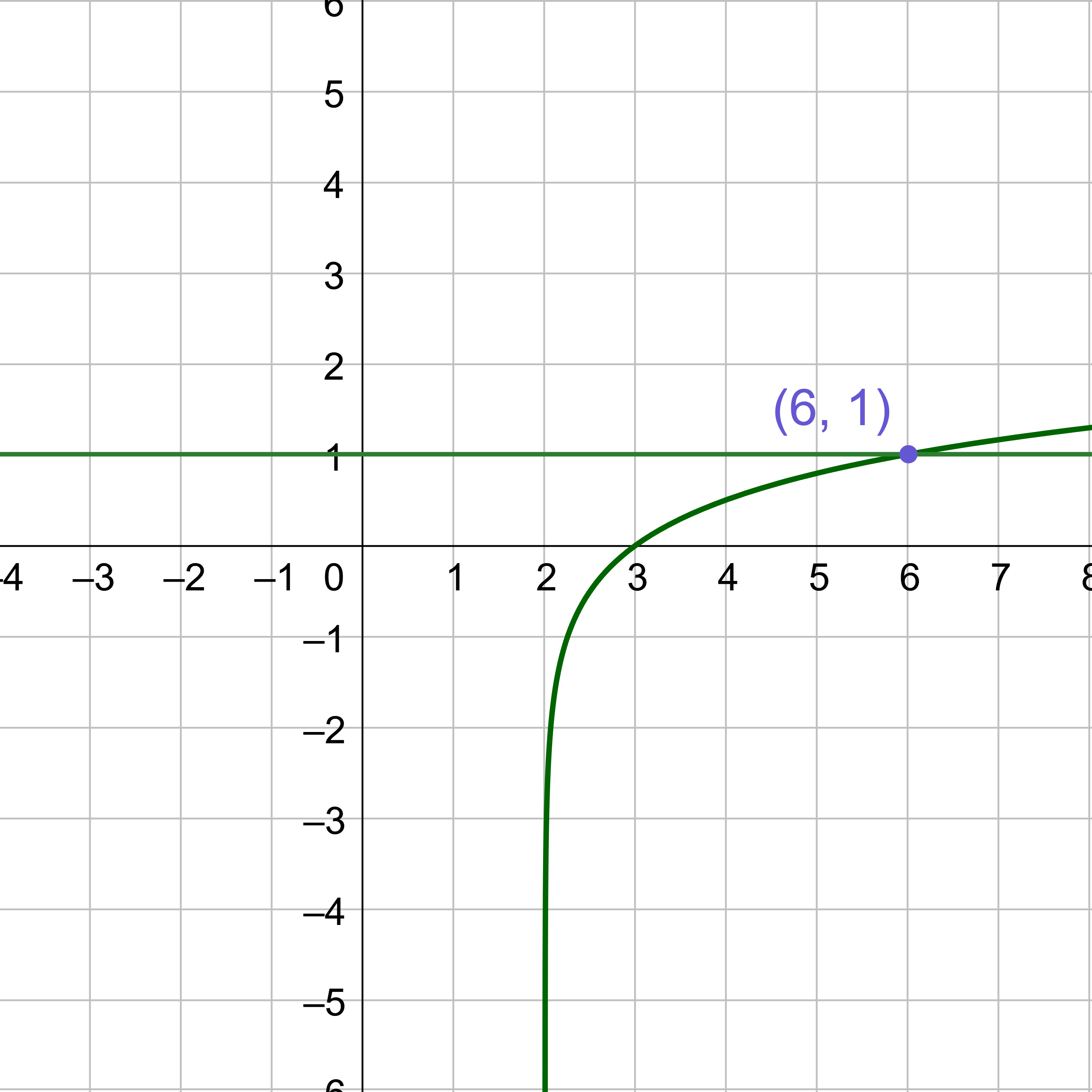
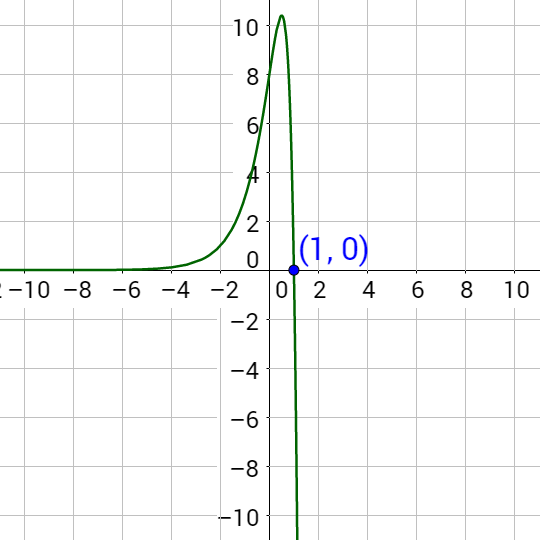
To solve this by graphing, subtract the 17 to make the right side 0.
5x + 2 − 17 = 0
Graph the left-hand side and find the x-intercept.
Since the x-intercept is (−0.240, 0), the solution is x = −0.240.
Solve 2ex + 1 − 4 = 12.
Solution
Start by isolating the exponential expression.
2ex + 1 − 4 = 12
2ex + 1 = 16
ex + 1 = 8
Take the logarithm of each side. Since the base of the exponential is e, use log base e.
ln ex + 1 = ln 8
The ln and base e cancel.
ln ex + 1 = ln 8
x + 1 = ln 8
x = (ln 8) − 1
x ≈ 1.079
Plug 1.079 into the original equation and see that both sides approximate 12, so it is the correct solution.
Analysis
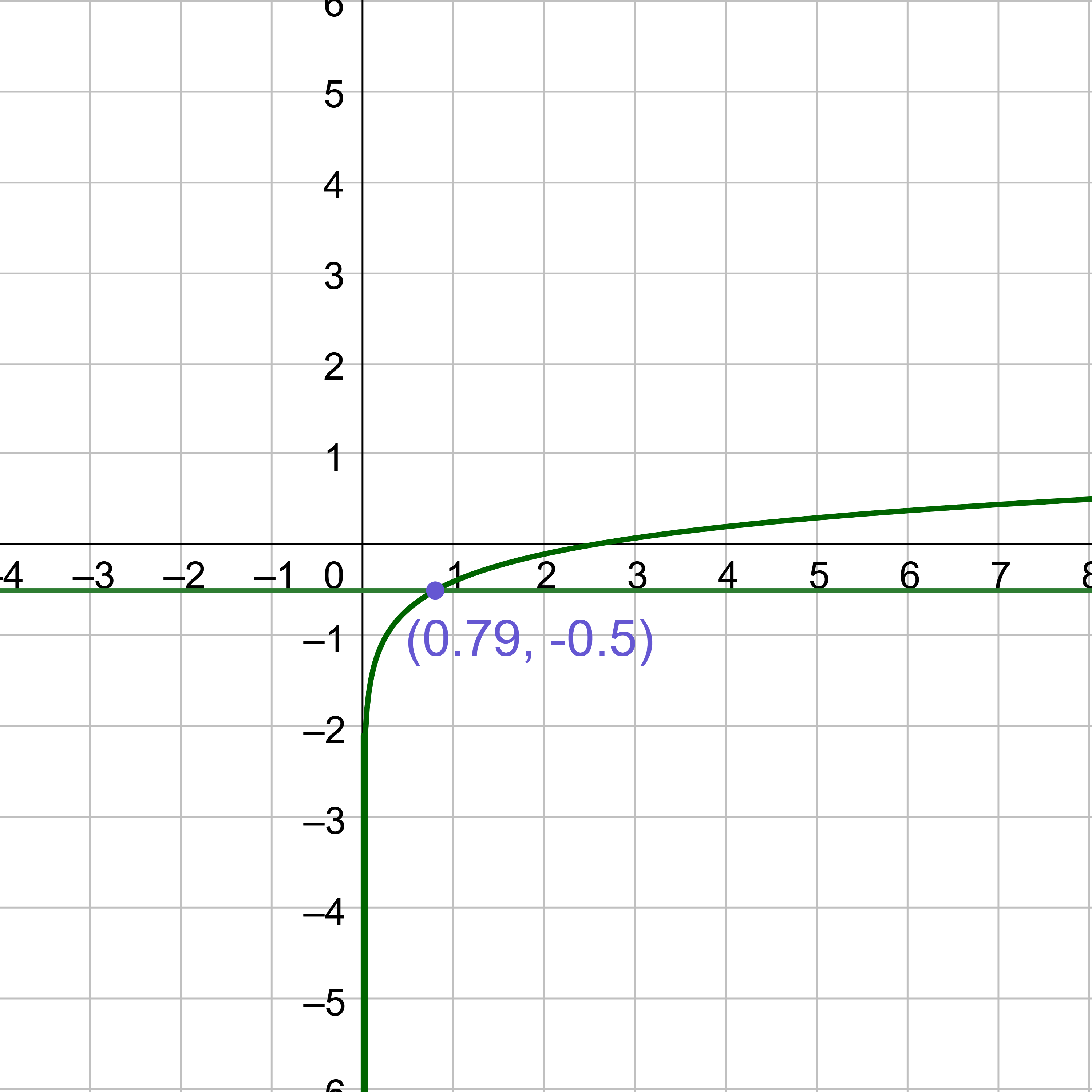
To solve this by graphing, subtract the 12 to make the right side 0.
2ex + 1 − 16 = 0
Graph the left-hand side and find the x-intercept.
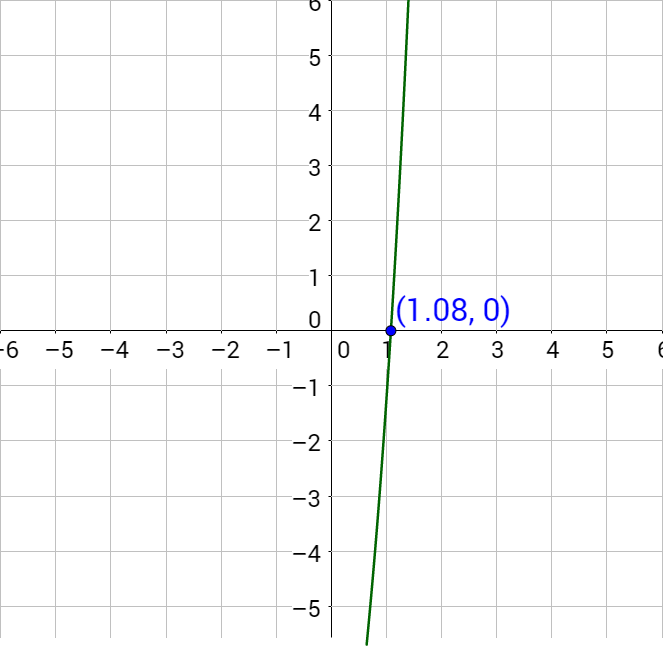
Since the x-intercept is (1.079, 0), the solution is x = 1.079.
Solve 3(2)x = 12.
Answer
x = 2
Since exponential functions are one-to-one, their inverses are also one-to-one. Logarithms are the inverse of exponential functions, so logarithmic functions are one-to-one.
To solve a logarithmic equation using the one-to-one property
Solve log3 (x + 1) = log3 (2x).
Solution
Each side of the equation is a logarithm with the same base, so the expressions in the logarithms are also equal.
log3 (x + 1) = log3 (2x)
x + 1 = 2x
1 = x
Check the solution by plugging 1 into the original equation. Both sides become log3 2, so it is the correct solution.
Analysis
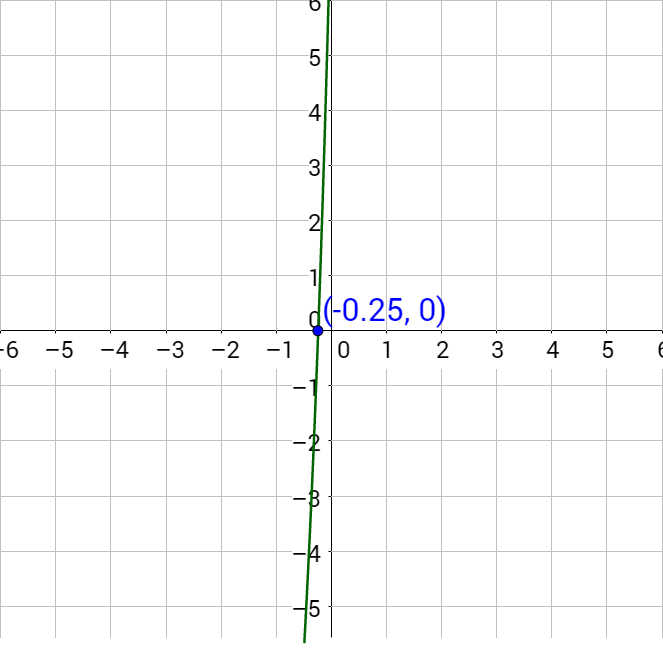
To solve this by graphing, subtract the log3 (2x) to make the right side 0.
log3 (x + 1) − log3 (2x) = 0
Graph the left-hand side and find the x-intercept.
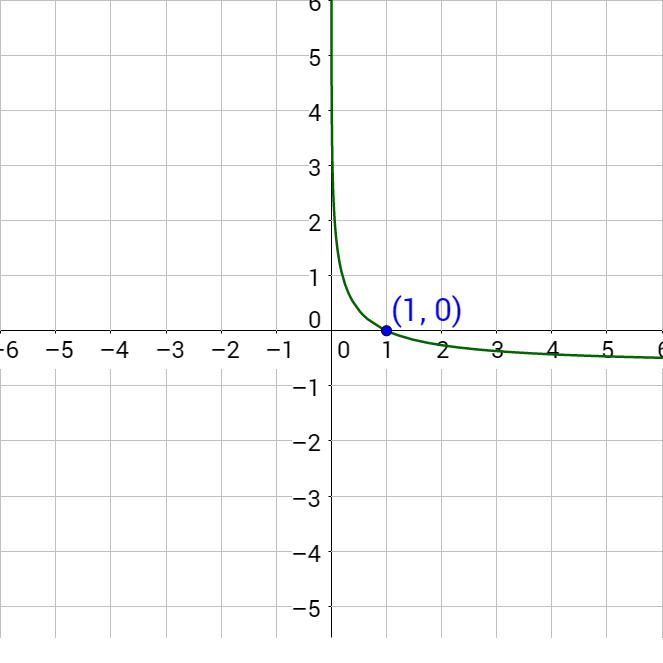
Since the x-intercept is (1, 0), the solution is x = 1.
Solve log4 x = log4 (3x − 7).
Answer
x = 7⁄2
When the equation does not have a single logarithm on both sides of the equation, use the general method of taking the inverse. The inverse of a logarithm is an exponential. To solve a general logarithmic function, make both sides the exponent of an exponential function using the base of the logarithm as the base of the exponential.
To solve a general logarithmic equation
Solve log3 (2x − 3) = 1.5.
Solution
The logarithm is already isolated, so start by exponentiating both sides. Use 3 as the base.
log3 (2x − 3) = 1.5
3log3 (2x − 3) = 31.5
Using the properties of logarithms, or the fact that logarithms and exponentials are inverses, the base 3 and log base 3 cancel. Then solve the resulting equation.
3log3 (2x − 3) = 31.5
2x − 3 = 31.5 ≈ 5.196
2x = 31.5 + 3 ≈ 8.196
x ≈ 4.098
Check the solution by plugging the answer into the original equation. Both sides approximate 1.5, so 4.098 is the solution.
Analysis
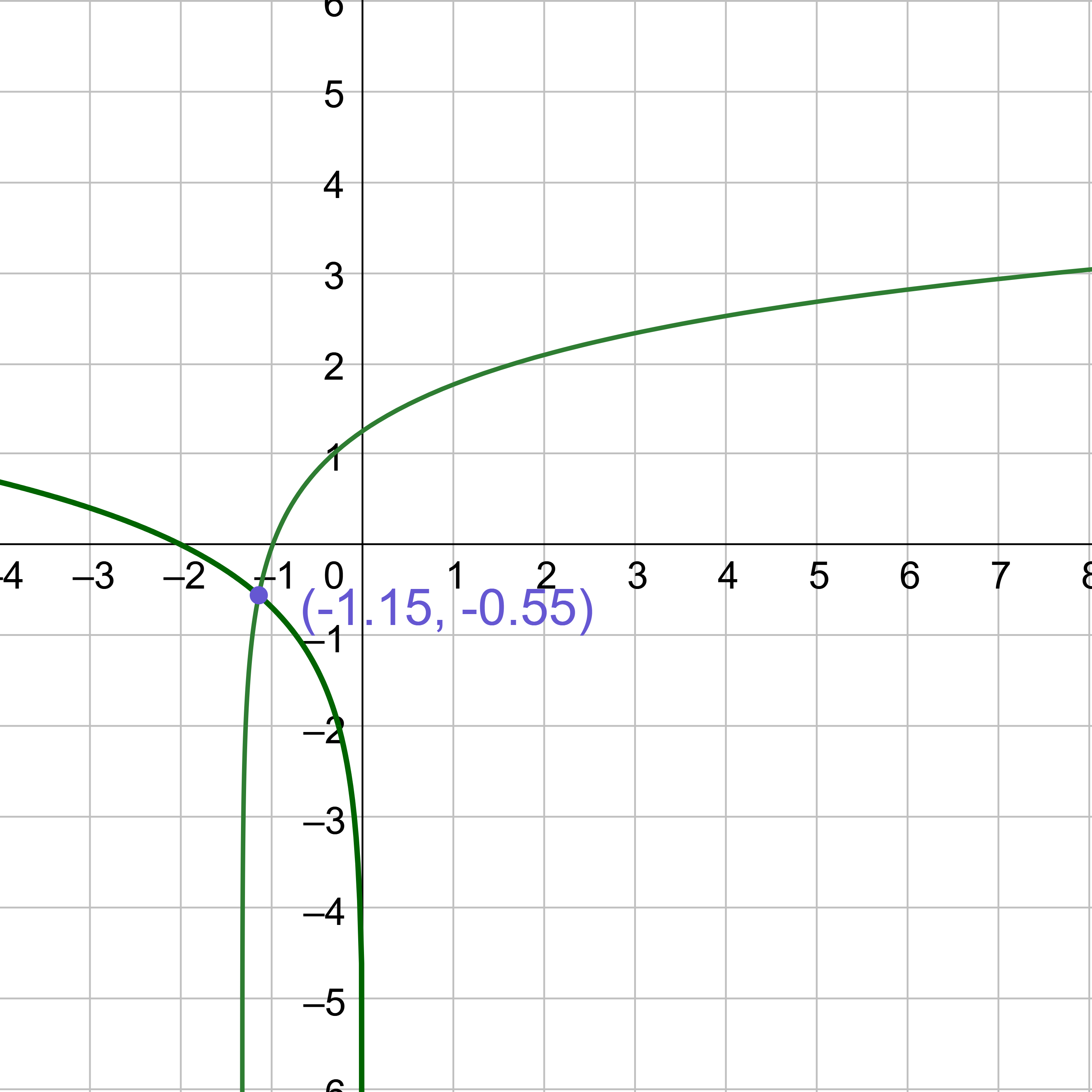
To solve this by graphing, subtract the log3 (2x) to make the right side 0.
log3 (2x − 3) − 1.5 = 0
Graph the left-hand side and find the x-intercept.
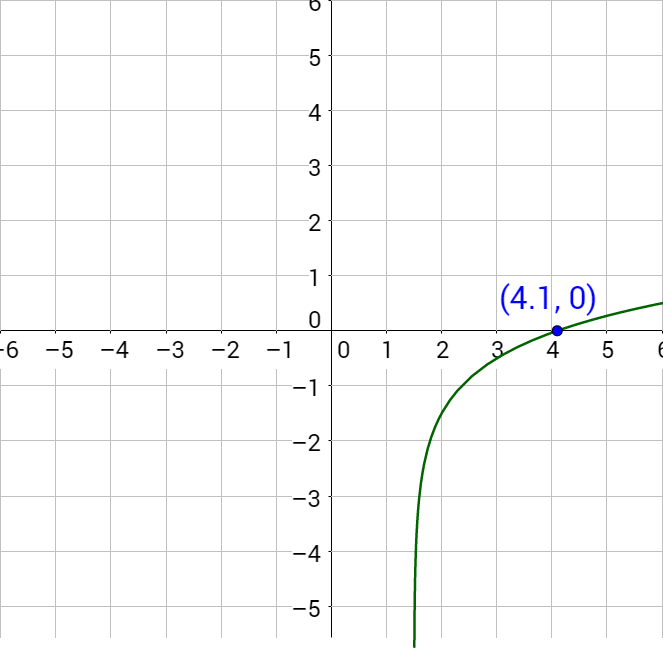
Since the x-intercept is (4.098, 0), the solution is x = 4.098.
Solve log2 (x − 2) + log2 (x) = 3.
Solution
The first step is to isolate the logarithm, but there are two of them. Condense the logarithms to make a single logarithm that is isolated on the left side of the equation.
log2 (x − 2) + log2 (x) = 3
log2 ((x − 2)(x)) = 3
log2 (x2 − 2x) = 3
The base of the logarithm is 2, so exponentiate both sides using 2 as the base. Then simplify and solve the resulting equation.
2log2 (x2 − 2x) = 23
2log2 (x2 − 2x) = 8
x2 − 2x = 8
x2 − 2x − 8 = 0
(x − 4)(x + 2) = 0
x − 4 = 0 and x + 2 = 0
x = 4 and x = −2
Check the solutions.
The solution is x = 4.
Analysis
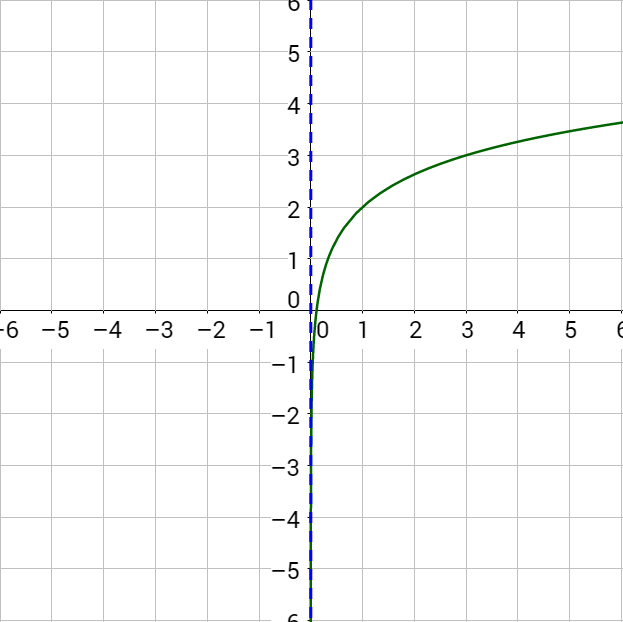
To solve this by graphing, subtract the 3 to make the right side 0.
log2 (x − 2) + log2 (x) − 3 = 0
Graph the left-hand side and find the x-intercept.
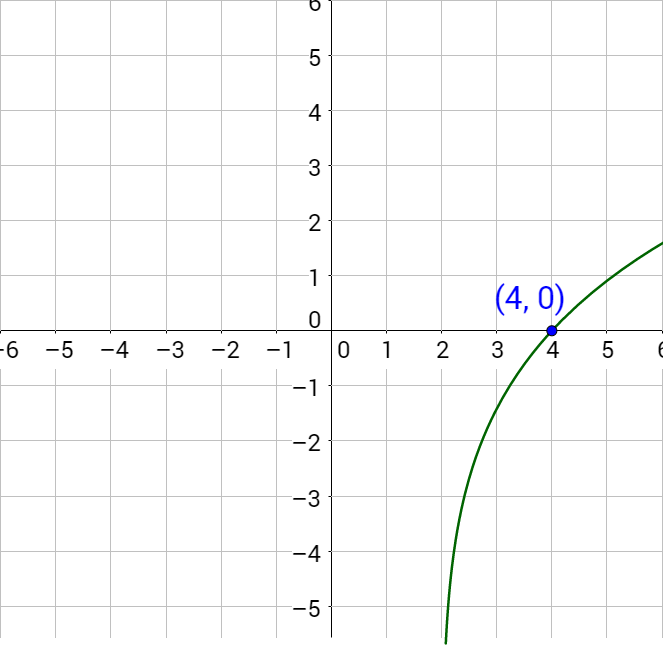
Since the x-intercept is (4, 0), the solution is x = 4.
Solve log3 (9x) = −log3 (x) + 4.
Answer
x = 3
During the Feeding of the 5,000, Jesus broke 5 loaves and 2 small fish and passed the pieces to the disciples who in turn passed them to the people. If each time the bread and fish were broken, Jesus broke them into two pieces each and there were 15,000 people, (a) write a model for the number of pieces of bread, P, after x number of breakings. Then (b) how many times did Jesus have to break a piece of bread before each person could have at least 1 piece?
Solution
Since the bread was always broken into two pieces, the amount of bread would always be multiplied by two. This is an exponential model with base 2. This gives the begin of the model.
P = 2x
However, at x = 0, or before any bread was broken, this model gives P = 20 = 1. But this should be 5 since there were originally 5 loaves, so multiply the model by 5.
P = 5(2)x
Since there were 15,000 people, then there will need to be 15,000 pieces of bread if each person is to get just one piece. So, P = 15,000 and solve for x.
15,000 = 5(2)x
Isolate the exponential expression by dividing by 5.
3,000 = 2x
Because this is a general exponential equation, solve it by taking the logarithm of each side. Choose base 2 since that is the base of the exponential.
log2 3,000 = log2 2x
log2 3,000 = log2 2x
log2 3,000 = x
x ≈ 11.55
Since the bread cannot be only half broken, the answer needs to be rounded up. Jesus would of had to break the bread about 12 times for each person to get just one piece. However, everyone got more than one piece. They got as much as they wanted with 12 big baskets of food left over. That means there was a lot of breaking of food happening, or maybe the miracle was done some other way.
To solve an exponential equation using the one-to-one property.
To solve an exponential equation using logarithms
To solve a logarithmic equation using the one-to-one property
To solve a general logarithmic equation
Helpful videos about this lesson.
