Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Let someone else praise you, and not your own mouth; an outsider, and not your own lips. Proverbs 27:2 NIV

4-04 Right Triangle Trigonometry and Identities

Mr. Wright teaches the lesson.

Summary: In this section, you will:

Use basic trigonometric identities.
Use right triangles to solve real world problems.

SDA NAD Content Standards (2018): PC.5.1, PC.5.3

radio towers. — Radio towers. (pixabay/susie)

Using right triangles and measurements of angles of elevation and depression, heights of towers and buildings can be calculated. But first, an introduction to trigonometric identities.

Trigonometric Identities

Trigonometric identities are equations that are true for every value of the variable in the domain. Identities provide ways rewrite and simplify complex trigonometric expressions and equations.

Basic Trigonometric Identities

Reciprocal Identities

$sin u = \frac{1}{csc u}$	$cos u = \frac{1}{sec u}$	$tan u = \frac{1}{cot u}$
$csc u = \frac{1}{sin u}$	$sec u = \frac{1}{cos u}$	$cot u = \frac{1}{tan u}$

Quotient Identities

tan u = \frac{sin u}{cos u}

cot u = \frac{cos u}{sin u}

Pythagorean Identities

sin² u + cos² u = 1

1 + tan² u = sec² u

cot² u + 1 = csc² u

Note: sin² u = (sin u)².

Cofunction Identities

sin (90° − u) = cos u	cos (90° − u) = sin u
tan (90° − u) = cot u	cot (90° − u) = tan u
sec (90° − u) = csc u	csc (90° − u) = sec u

The reciprocal identities were already introduced in previous lessons. Refer back to lessons 4-02 and 4-03. The other identities are explained below.

Quotient Identities

On the unit circle, sin θ = y and cos θ = x. Divide these equations.

$\frac{\sin θ}{\cos θ} = \frac{y}{x} = \tan θ$

Thus,

$\tan θ = \frac{\sin θ}{\cos θ}$

And, the reciprocal is also true.

$\cot θ = \frac{\cos θ}{\sin θ}$

Pythagorean Identities

Think of drawing a right triangle on the unit circle so that one leg is on the x-axis, the other leg is vertical, and the hypotenuse is a radius of the circle.

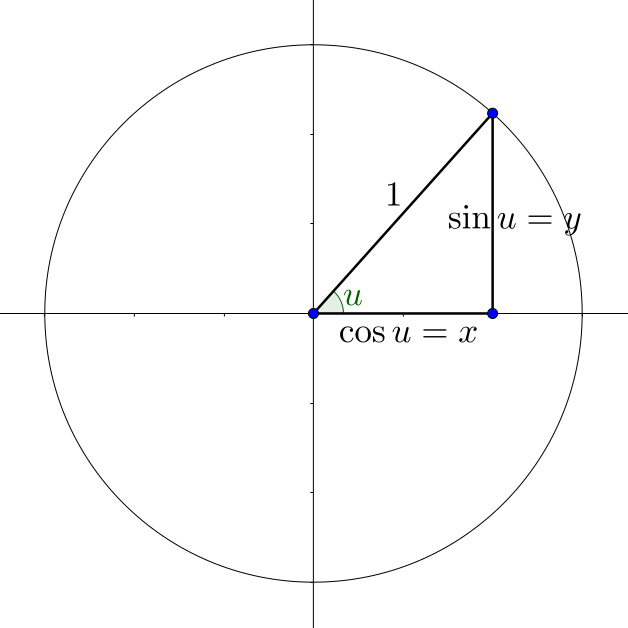
The horizontal leg is the x-coordinate of the point, but on the unit circle cos θ = x. The vertical leg is the y-coordinate of the point, but on the unit circle sin θ = y. The hypotenuse is a radius of the unit circle, so its length is 1. Apply the Pythagorean Theorem.

x² + y² = 1²

cos² θ + sin² θ = 1

Divide this by either sin² θ or cos² θ to get the other two Pythagorean identities.

Cofunction Identities

Imagine a right triangle where one acute angle measure is u. The two acute angles in a right triangle are complementary. If the other acute angle is v, see figure 3, then

u + v = 90°

Solve for v.

v = 90° − u

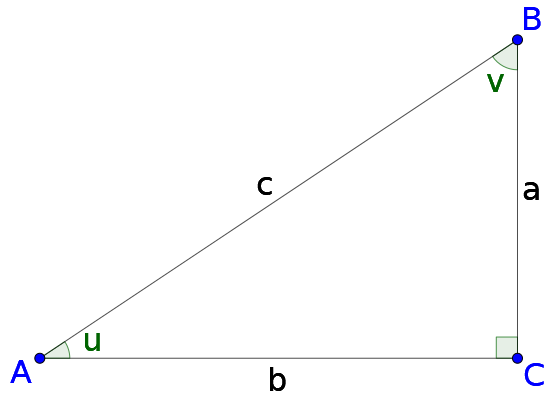
If the sides of the triangle are a, b, and c as in figure 3, then $\sin u = \frac{a}{c}$ and $\cos v = \frac{a}{c}$ . Thus sin u = cos v. Since v = 90° − u,

sin u = cos (90° − u)

The other cofunction identities have similar logic.

Use Trigonometric Identities

Let θ be an acute angle and cos θ = 0.3. Find the values of a) sin θ and b) tan θ using trigonometric identities.

Solution

We know cosine and want to find sine, so pick an identity that has both:

sin² θ + cos² θ = 1
sin² θ + (0.3)² = 1
sin² θ = 0.91
sin θ ≈ 0.9539
We know cosine and want to find tangent. From part a we also know sine, so we can use a quotient identity.

$\begin{matrix} tan θ = \frac{sin θ}{cos θ} \\ tan θ = \frac{0.9539}{0.3} \\ tan θ \approx 3.1783 \end{matrix}$

Use Trigonometric Identities

Let α be an acute angle and csc α = 2. Find a) sin α and b) cot α using trigonometric identities.

Solution

We know cosecant and want to find sine, so use an identity with both of those.

$\begin{matrix} sin α = \frac{1}{csc α} \\ sin α = \frac{1}{2} \end{matrix}$
We know cosecant and want to find cotangent, so use an identity with both of them.

$\begin{matrix} {cot}^{2} α + 1 = {csc}^{2} α \\ {cot}^{2} α + 1 = 2^{2} \\ cot α = \sqrt{3} \end{matrix}$

Let β be an acute angle and tan β = ½. Find a) cot β and b) sec β.

Answers

2; $\frac{\sqrt{5}}{2}$

Applications with Right Triangles

Some real-world problems can be solved by drawing right triangles and finding unknown lengths. Other problems use angles of elevation and depression.

Angles of Elevation and Depression

The angle of elevation is the angle between the horizontal up to an object.

The angle of depression is the angle between the horizontal down to an object.

Solve a Problem with a Right Triangle

A 8-foot step ladder actually is not 8-feet high. The size of a step ladder is actually the length of the rails that the steps are attached to. When the ladder is in use the rails are slanted so the height is less. If the rails of an 8-foot step ladder make an angle of 50° with the ground, how high is the top of the ladder from the ground?

Solution

Draw a right triangle using the rails of the ladder as the hypotenuse. The hypotenuse is 8 feet long and the angle with the ground is 50°.

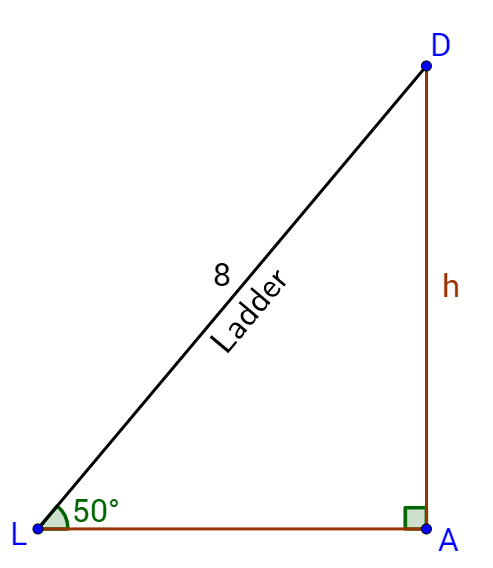
The hypotenuse and one angle are known and the opposite leg is the unknown. The formula of sine from lesson 4-03 has those three parts. Use sine to solve the problem.

$\begin{matrix} sin L = \frac{opp}{hyp} \\ sin 50 ° = \frac{h}{8} \\ 8 sin 50 ° = h \\ h \approx 6.12 \end{matrix}$

The height of the ladder is actually about 6.12 feet.

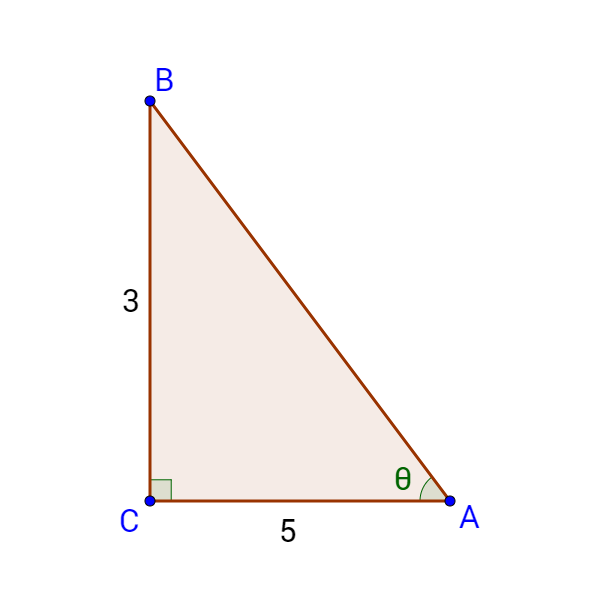
Find the length of side a in figure 6.

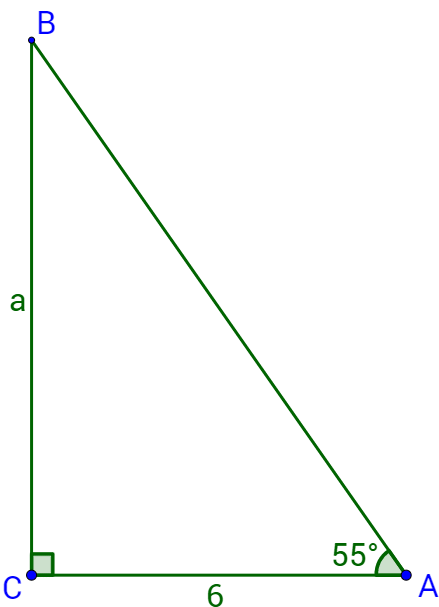
Answer

8.57

Angle of Elevation

To find the height of a tree, a person walks to a point 30 feet from the base of the tree. She measures an angle of elevation of 57° between a line of sight to the top of the tree and the ground. Find the height of the tree.

Solution

The adjacent leg and angle are known. The height is the unknown. Use a trigonometric formula that has those three quantities.

$\begin{matrix} tan θ = \frac{opp}{adj} \\ tan 57 ° = \frac{h}{30} \\ 30 tan 57 ° = h \\ h \approx 46.20 \end{matrix}$

The height of the tree is about 46 feet.

Angle of Elevation

A hiker is standing on mesa 80 feet above the desert floor. The angle of depression to a creek is 50°. Farther away, the angle of depression to a horse is 30°. How far apart are the horse and the creek?

Solution

Draw a picture to visualize the situation.

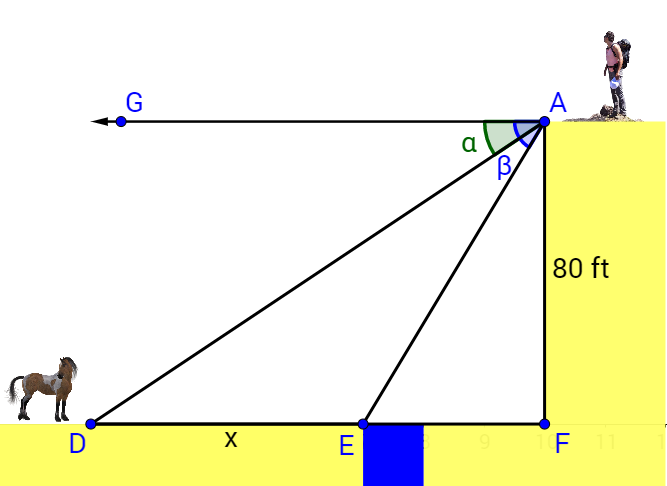
This will be a two part problem. First, since $\overline{AG}$ and $\overline{DF}$ are parallel, then ∠α and ∠ADF are congruent. So are ∠β and ∠AEF.

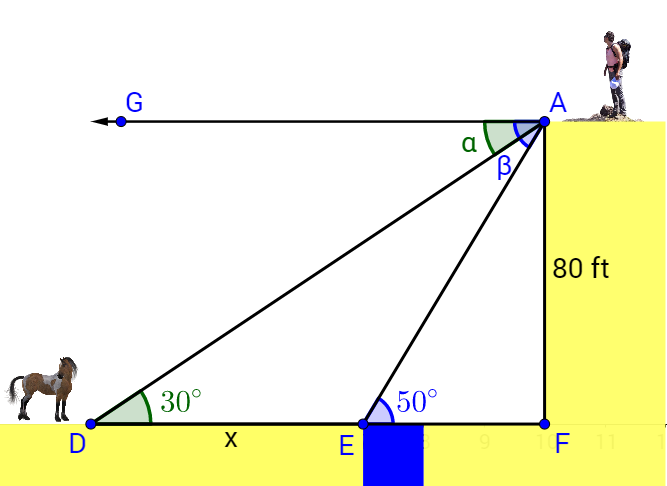
Start by finding the length of DF using ΔADF.

$\begin{matrix} tan u = \frac{opp}{adj} \\ tan 30 ° = \frac{80}{DF} \\ DF = \frac{80}{tan 30 °} \\ DF \approx 138.56 \end{matrix}$

Now find the length of EF using ΔAEF.

$\begin{matrix} tan u = \frac{opp}{adj} \\ tan 50 ° = \frac{80}{EF} \\ EF = \frac{80}{tan 50 °} \\ EF \approx 67.13 \end{matrix}$

Now subtract to find x.

x = DF − EF
x = 138.56 − 67.13 = 71.43

The horse is approximately 71 feet from the creek.

A student is observing a radio tower. Two sets of guy wires are attached at the same spot on the ground 50 feet away from the tower. The other ends of the guy wires are attached to the tower at different points. If the angles of elevation of the guy wires are 50° and 70°, how far apart are they attached on the tower?

Answer

77.8 ft

Lesson Sumamry

Basic Trigonometric Identities

Reciprocal Identities

$sin u = \frac{1}{csc u}$	$cos u = \frac{1}{sec u}$	$tan u = \frac{1}{cot u}$
$csc u = \frac{1}{sin u}$	$sec u = \frac{1}{cos u}$	$cot u = \frac{1}{tan u}$

Quotient Identities

tan u = \frac{sin u}{cos u}

cot u = \frac{cos u}{sin u}

Pythagorean Identities

sin² u + cos² u = 1

1 + tan² u = sec² u

cot² u + 1 = csc² u

Note: sin² u = (sin u)².

Cofunction Identities

sin (90° − u) = cos u	cos (90° − u) = sin u
tan (90° − u) = cot u	cot (90° − u) = tan u
sec (90° − u) = csc u	csc (90° − u) = sec u

Angles of Elevation and Depression

The angle of elevation is the angle between the horizontal up to an object.

The angle of depression is the angle between the horizontal down to an object.

Angles of Elevation and Depression

Helpful videos about this lesson.

Mr. Wright Teaches the Lesson (https://youtu.be/PtDRUYvpOn4)
Pythagorean Identities (http://openstaxcollege.org/l/pythagiden)

Practice Exercises

Explain the cofunction identity.
Let θ be an acute angle. Use the given function value with trigonometric identities to evaluate the given function.
If sin θ = 0.9, find a) cos θ and b) csc θ.
If sin θ = 0.25, find a) sin(90° − θ) and b) tan θ.
If sec θ = 1.45, find a) cos θ and b) tan θ.
If cos θ = 0.6, find a) sin θ and b) cot θ.
If csc θ = 10, find a) sin θ and b) csc (90° − θ).
Problem Solving
A 20-ft ladder leans against a building so that the angle between the ladder and the ground is 75°. How high up the building does the ladder reach?
A 30-ft ladder leans against a building so that the angle between the ladder and the ground is 70°. How far from the building is the base of the ladder?
The angle of elevation to the top of the Willis Tower is 33.2° when you are a half-mile from the base of the tower. How high is the tower?
*If the Empire State Building is 1250 ft high and the angle of the elevation to the top is 52°, how far from the building are you?
A group of civil engineers wants to build a bridge over a canyon, but they do not know how wide the canyon is. They raise different tall objects up beside the canyon until one of them casts a shadow to the other side of the canyon. The height of the object is 80 ft and they estimate the angle of elevation of the sun is 35°. Roughly, how wide is the canyon? (Ben P)
A tall pine tree grows vertically. If Sam is 50 feet from the tree and measures the angle of elevation as 80°, how tall is the tree?
A large advertising banner hangs on the side of a building. Duane works in a neighboring building 75 feet away and measures to angle of elevation to the top of the banner as 50° and the angle of depression to the bottom as 20°. How long is the banner?
Marie is standing on a platform waiting to ride a roller coaster. She measures the angle of depression to the bottom of the long hill as 13° and the angle of elevation to the top of the hill as 52°. If she is 110 feet away, how high is the hill?
A steeple is on top of a church. Marco stands 52 ft from the church and measures the angle of elevation to the base of the steeple as 44°. He measures the angle of elevation to the top of the steeple as 56°. How tall is the steeple?
Philip is standing on Inspiration Point in Arcadia Scenic Turnout 800 feet above Lake Michigan. He can see two ship, one behind the other. If the angle of depression to the closer ship is 18° and the farther ship is 15°, how far apart are the ships?
Mixed Review
(4-03) Use a special right triangle to evaluate a) tan 30° and b) $sec \frac{π}{4}$ .
(4-03) Evaluate the six trigonometric functions for the given angle.
(4-02) Evaluate the six trigonometric functions for $\frac{4 π}{3}$ using the unit circle.
(4-01) A car with a 30-inch diameter wheels is traveling at 50 mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
(3-02) What is the intensity of a loud stereo blaring music at 95 dB?

Answers

For example, the sine of an angle is equal to the cosine of its complement; the cosine of an angle is equal to the sine of its complement.
0.4359; 10⁄9
0.9682; 0.2582
0.6897; 1.05
0.8; 0.75
0.1; 1.0050
19.3 ft
10.3 ft
1728 ft
977 ft
114 ft
284 ft
116.7 ft
166.2 ft
26.9 ft
523 ft
$\frac{\sqrt{3}}{3}$ ; $\sqrt{2}$
$sin θ = \frac{3 \sqrt{34}}{34}, cos θ = \frac{5 \sqrt{34}}{34}, tan θ = \frac{3}{5}, csc θ = \frac{\sqrt{34}}{3}, sec θ = \frac{\sqrt{34}}{5}, cot θ = \frac{5}{3}$
$sin \frac{4 π}{3} = - \frac{\sqrt{3}}{2}, cos \frac{4 π}{3} = - \frac{1}{2}, tan \frac{4 π}{3} = \sqrt{3}, csc \frac{4 π}{3} = - \frac{2 \sqrt{3}}{3}, sec \frac{4 π}{3} = - 2, cot \frac{4 π}{3} = \frac{\sqrt{3}}{3}$
3520 rad/min; 560.2 rev/min
0.00316 W/m²