Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Jesus straightened up and asked her, “Woman, where are they? Has no one condemned you?”
“No one, sir,” she said.
“Then neither do I condemn you,” Jesus declared. “Go now and leave your life of sin.” John 8:10-11 NIV

4-05 Trigonometric Functions of Any Angle

Mr. Wright teaches the lesson.

Summary: In this section, you will:

Evaluate trigonometric functions of any angle.
Find reference angles.

SDA NAD Content Standards (2018): PC.5.3

Berlin Radio tower and town hall. — London Eye. (pixabay/skeeze)

The London Eye is a Ferris wheel with a diameter of 394 feet. By combining the ideas of the unit circle and right triangles, the location of any capsule on the Eye can be described with trigonometry.

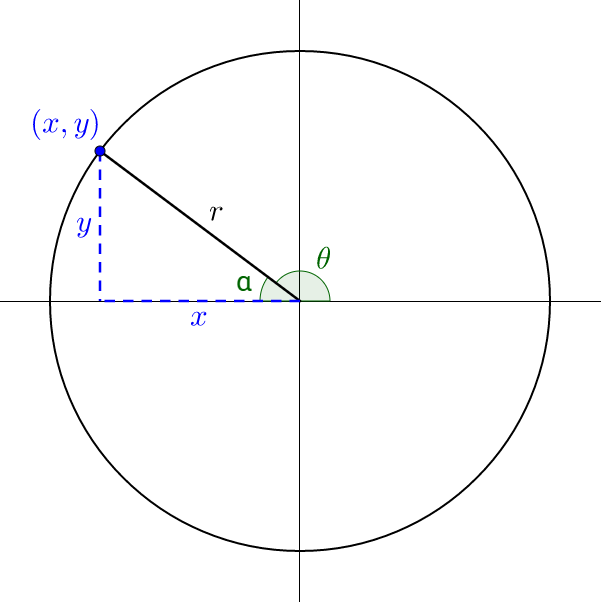
Trigonometric Functions of Angles on Circles with r ≠ 1

Lesson 4-02 looked at the unit circle. Lesson 4-03 explored right triangle trigonometry. To combine these ideas, consider a circle where r ≠ 1. Pick a point on the circle. A right triangle can be drawn to the point where one acute angle is at the point, the other acute angle is at the origin, and the right angle is on the x-axis.

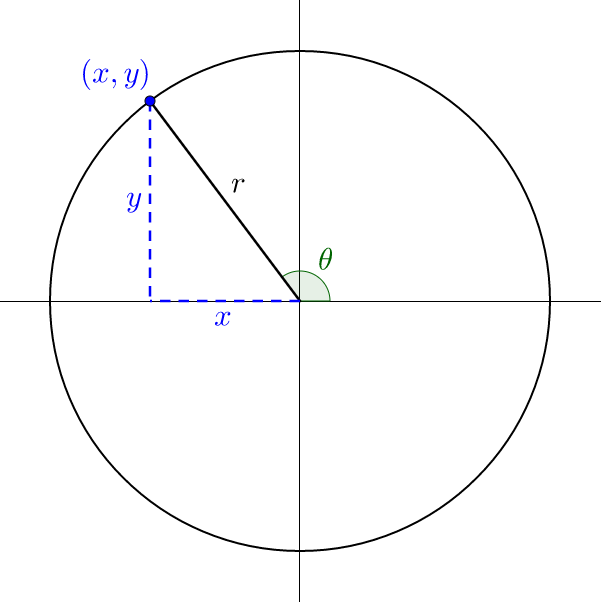
Right triangle drawn to a point on a circle.

Comparing the unit circle formulas and the right triangle formulas develops the formulas for any angle. For example, consider sin θ.

$\begin{array}{l} sin θ = y & Unit Circle \\ sin θ = \frac{opp}{hyp} & Right Triangle \\ sin θ = \frac{y}{r} & Apply the right triangle formula for the acute angle by the origin. \end{array}$

Notice the last equation matches the unit circle formula with r = 1. All the unit circle formulas can be similarly modified.

Trigonometric Functions of Any Angle

$sin θ = \frac{y}{r}$	$csc θ = \frac{r}{y}$
$cos θ = \frac{x}{r}$	$sec θ = \frac{r}{x}$
$tan θ = \frac{y}{x}$	$cot θ = \frac{x}{y}$

where θ is an angle in standard position with point (x, y) on the terminal side and $r = \sqrt{x^{2} + y^{2}}$

Evaluate Trigonometric Functions

Let (−4, 3) be a point on the terminal side of angle θ. Evaluate the six trigonometric functions of θ.

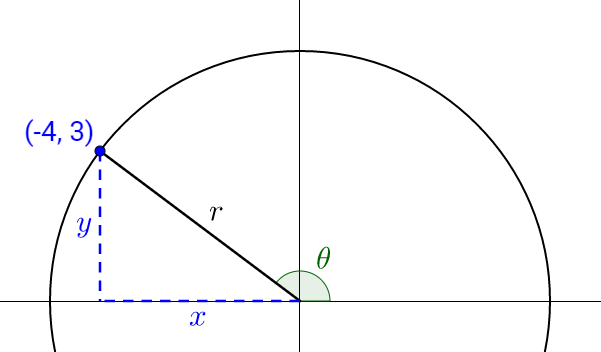
Solution

Find r.

$\begin{array}{l} r = \sqrt{x^{2} + y^{2}} \\ r = \sqrt{{(- 4)}^{2} + 3^{2}} \\ r = 5 \end{array}$

Now use the trigonometric formulas.

$\begin{array}{l} sin θ = \frac{y}{r} = \frac{3}{5} & csc θ = \frac{r}{y} = \frac{5}{3} \\ cos θ = \frac{x}{r} = - \frac{4}{5} & sec θ = \frac{r}{x} = - \frac{5}{4} \\ tan θ = \frac{y}{x} = - \frac{3}{4} & cot θ = \frac{y}{r} = - \frac{4}{3} \end{array}$

If (4, −8) is a point on the terminal side of angle α in standard position, evaluate the six trigonometric functions of α.

Answers

$\begin{array}{l} sin α = - \frac{2 \sqrt{5}}{5} & csc α = - \frac{\sqrt{5}}{2} \\ cos α = \frac{\sqrt{5}}{5} & sec α = \sqrt{5} \\ tan α = - 2 & cot α = - \frac{1}{2} \end{array}$

Evaluate Trigonometric Functions of Quadrantal Angles

Evaluate cos 270° and csc π.

Solution

270° and π radians terminal sides are both on an axis. Start by choosing a point on the terminal sides of the angle.

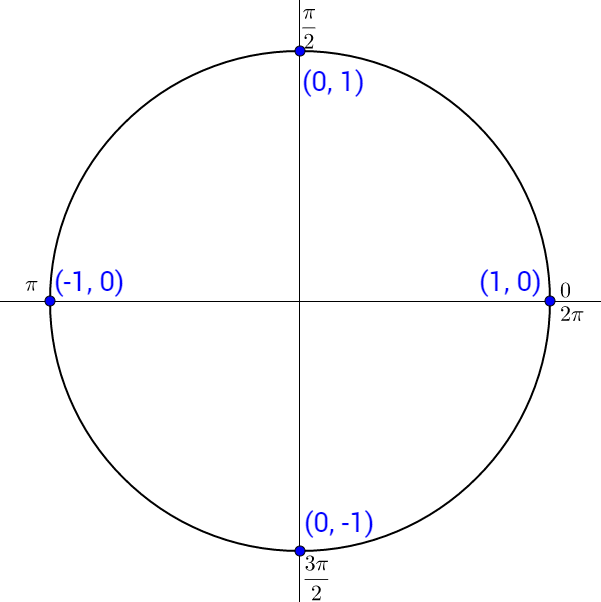
Now apply the trigonometric formulas with r = 1.

$\begin{array}{l} cos θ = \frac{x}{r} & csc θ = \frac{r}{y} \\ cos 270 ° = \frac{0}{1} = 0 & csc π = \frac{1}{0} = undefined \end{array}$

Evaluate sin 90° and cot 0.

Answer

1; undefined

Signs of Trigonometric Functions in the Quadrants

By filling in the negative signs for x and y from the quadrants into the trigonometric formulas a pattern develops. For example, consider sine and cosine in quadrant II where the x is negative and y is positive.

$sin θ = \frac{y}{r}$	Since the y and r are both positive, sine is positive.
$cos θ = \frac{x}{r}$	Since the x is negative and r are both positive, cosine is negative.

All the trigonometric functions' signs can be similarly determined for all four quadrants. Figure 5 shows which trigonometric functions are positive in each quadrant.

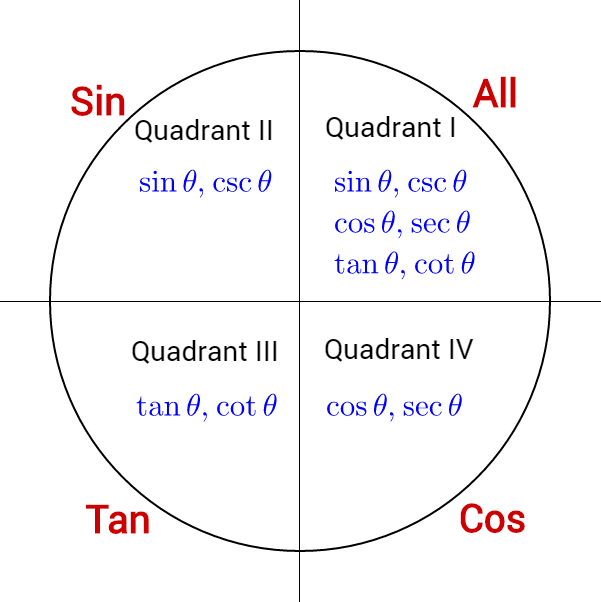
Positive trigonometric functions in each quadrant.

Evaluate Trigonometric Functions

If $cos θ = - \frac{8}{17}$ and sin θ < 0, find tan θ and csc θ.

Solution

$cos θ = \frac{x}{r} = - \frac{8}{17}$

Since the r is always positive, r = 17 and x = −8. Use the Pythagorean Theorem to find y.

$\begin{array}{l} x^{2} + y^{2} = r^{2} \\ {(- 8)}^{2} + y^{2} = 17^{2} \\ y^{2} = 225 \\ y = \pm 15 \end{array}$

Since sin θ < 0 and $sin θ = \frac{y}{r}$ , y must be negative. So, y = −15.

Now it is known that x = −8, y = −15, and r = 17. Since both x and y are negative, the angle terminates in quadrant III where tan θ and cot θ are positive. We could have also looked for a quadrant where both sin θ and cos θ were negative which is quadrant III. Now fill in the trigonometric formulas.

$\begin{array}{l} sin θ = \frac{y}{r} = - \frac{15}{17} & csc θ = \frac{r}{y} = - \frac{17}{15} \\ cos θ = \frac{x}{r} = - \frac{8}{17} & sec θ = \frac{r}{x} = - \frac{17}{8} \\ tan θ = \frac{y}{x} = \frac{15}{8} & cot θ = \frac{y}{r} = \frac{8}{15} \end{array}$

If $sin θ = - \frac{\sqrt{5}}{3}$ and cos θ > 0, find tan θ and cos θ.

Answers

$tan θ = - \frac{\sqrt{5}}{2}$ ; $cos θ = \frac{2}{3}$

Reference Angles

Since the formula from the unit circle and the right triangles give the same expressions for example 1, the acute angle by the origin in the triangle and the angle in standard position must give the same values of the trigonometric functions. Those acute angles are useful and called reference angles.

Reference Angles

The reference angle is the angle between the terminal side of an angle in standard position and the nearest x-axis. Reference angles are always less than $\frac{π}{2}$ . The values of the trigonometric functions of the angle in standard position equal values of the trigonometric functions of the reference angle with the appropriate negative signs for the quadrant.

To find the reference angle

Determine the measure of the angle whose terminal side is on the x-axis nearest the terminal side of the given angle.
Subtract the measures of the given angle and the x-axis angle.

Find a Reference Angle

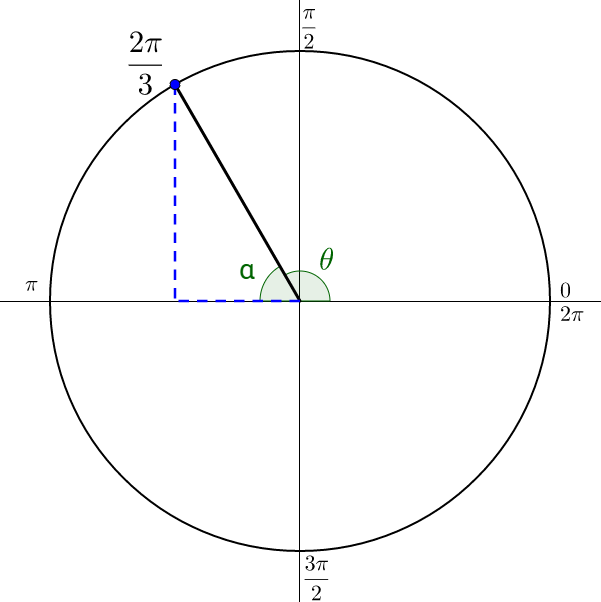
Find the reference angle for a) $\frac{7 π}{6}$ , b) $\frac{2 π}{3}$ , c) $\frac{π}{4}$ , and d) $\frac{7 π}{4}$ .

Solution

$\frac{7π}{6}$

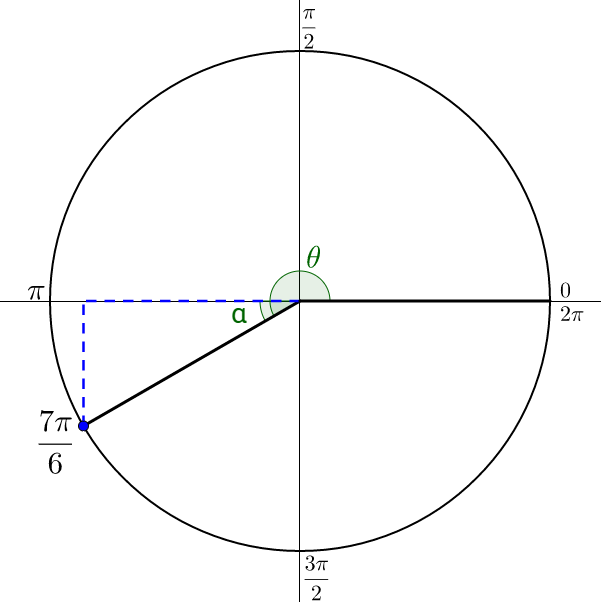
It is easiest to start by stretching a graph of the angle in standard position like in figure 7.

The x-axis angle nearest the terminal side of angle θ is π. Subtract π and $\frac{7 π}{6}$ to find the reference angle.

$\begin{array}{l} \frac{7 π}{6} - π \\ \frac{7 π}{6} - \frac{6 π}{6} = \frac{π}{6} \end{array}$

The reference angle is $\frac{π}{6}$ .
$\frac{2π}{3}$

The graph of $\frac{2 π}{3}$ is in figure 8.

The x-axis angle nearest the terminal side of angle θ is π. Subtract π and $\frac{2 π}{3}$ to find the reference angle.

$\begin{array}{l} π - \frac{2 π}{3} \\ \frac{3 π}{3} - \frac{2 π}{3} = \frac{π}{3} \end{array}$

The reference angle is $\frac{π}{3}$ .
$\frac{π}{4}$

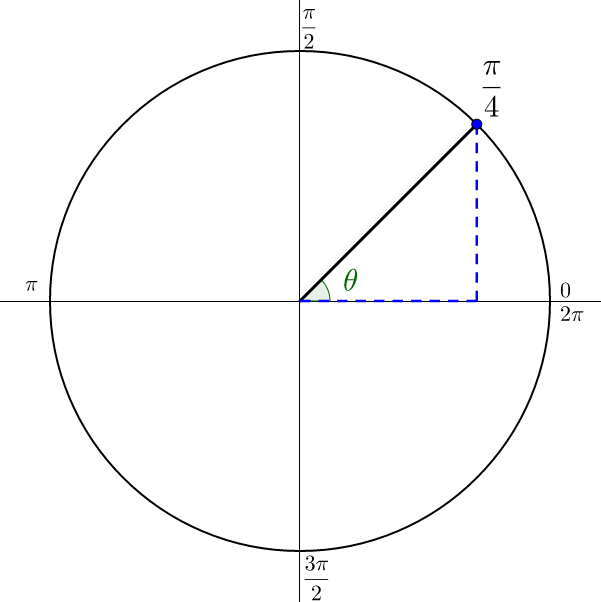
The graph of $\frac{π}{4}$ is in figure 9.

The x-axis angle nearest the terminal side of angle θ is 0. Subtract 0 and $\frac{π}{4}$ to find the reference angle.

$\begin{array}{l} \frac{π}{4} - 0 = \frac{π}{4} \end{array}$

The reference angle is $\frac{π}{4}$ .
$\frac{7π}{4}$

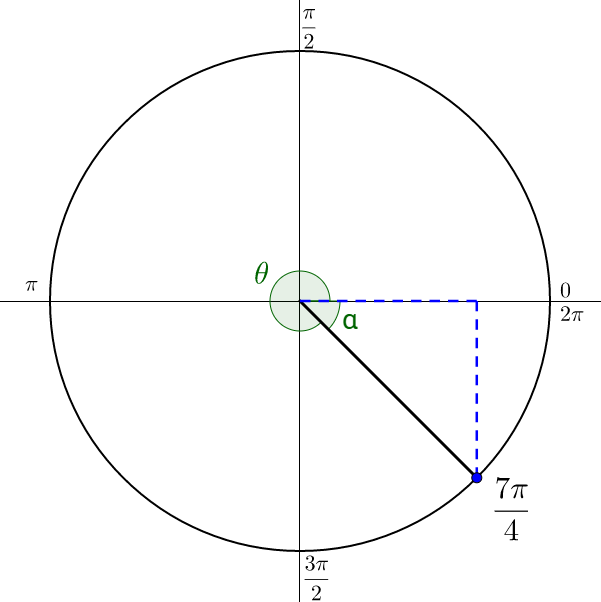
The graph of $\frac{7 π}{4}$ is in figure 10.

The x-axis angle nearest the terminal side of angle θ is 2π. Subtract 2π and $\frac{7 π}{4}$ to find the reference angle.

$\begin{array}{l} 2 π - \frac{7 π}{4} \\ \frac{8 π}{4} - \frac{7 π}{4} = \frac{π}{4} \end{array}$

The reference angle is $\frac{π}{4}$ .

Find the reference angle for $\frac{5 π}{3}$ .

Answer

$\frac{π}{3}$

Trigonometric Functions of Real Numbers

All the ideas from this lesson can be combined to evaluate trigonometric functions of any real number.

Evaluate Trigonometric Functions of Any Real Number

Consider the number to be an angle, θ.
If θ is not between 0 and 2π, find a coterminal angle between 0 and 2π by adding or subtracting 2π.
Find the reference angle.
Evaluate the trigonometric function of the reference angle using special right triangles (lesson 4-04) or the unit circle (lesson 4-02).
Apply a negative sign as needed based on the quadrant θ is in.

Use Reference Angles

Evaluate a) $cos \frac{7 π}{6}$ , b) $sin \frac{2 π}{3}$ , c) $tan \frac{13 π}{4}$ , and d) $sin (- \frac{7 π}{4})$ .

Solution

$\frac{7 π}{6}$ is between 0 and 2π, so start by finding the reference angle. Example 4 found the reference angle of $\frac{7 π}{6}$ is $\frac{π}{6}$ . Evaluate the function of the reference angle using special right triangles or the unit circle.

$cos \frac{π}{6} = \frac{\sqrt{3}}{2}$

$\frac{7 π}{6}$ is in quadrant III and cosine is negative in quadrant III, so $cos \frac{7 π}{6} = - \frac{\sqrt{3}}{2}$ .
$\frac{2 π}{3}$ is between 0 and 2π, so start by finding the reference angle. Example 4 found the reference angle of $\frac{2 π}{3}$ is $\frac{π}{3}$ . Evaluate the function of the reference angle using special right triangles or the unit circle.

$sin \frac{π}{3} = \frac{\sqrt{3}}{2}$

$\frac{2 π}{3}$ is in quadrant II and sine is positive in quadrant II, so $sin \frac{2 π}{3} = \frac{\sqrt{3}}{2}$ .
$\frac{13 π}{4}$ is not between 0 and 2π, so begin by finding a coterminal angle between 0 and 2π.

$\begin{array}{l} \frac{13 π}{4} - 2 π = \\ \frac{13 π}{4} - \frac{8 π}{4} = \frac{5 π}{4} \end{array}$

Find the reference angle. $\frac{5 π}{4}$ is in quadrant III and closest x-axis angle is π.

$\begin{array}{l} \frac{5 π}{4} - π = \\ \frac{5 π}{4} - \frac{4 π}{4} = \frac{π}{4} \end{array}$

Evaluate the function of the reference angle using special right triangles or the unit circle.

$tan \frac{π}{4} = 1$

$\frac{13 π}{4}$ which is coterminal with $\frac{5 π}{4}$ is in quadrant III and tangent is positive in quadrant III, so $tan \frac{13 π}{4} = 1$ .
$- \frac{7 π}{4}$ is not between 0 and 2π, so begin by finding a coterminal angle between 0 and 2π.

$\begin{array}{l} - \frac{7 π}{4} + 2 π = \\ - \frac{7 π}{4} + \frac{8 π}{4} = \frac{π}{4} \end{array}$

Find the reference angle. $\frac{π}{4}$ is in quadrant I and closest x-axis angle is 0.

$\begin{array}{l} \frac{π}{4} - 0 = \frac{π}{4} \end{array}$

Evaluate the function of the reference angle using special right triangles or the unit circle.

$sin \frac{π}{4} = \frac{\sqrt{2}}{2}$

$- \frac{7 π}{4}$ which is coterminal with $\frac{π}{4}$ is in quadrant I and sine is positive in quadrant I, so $sin (- \frac{7 π}{4}) = \frac{\sqrt{2}}{2}$ .

Evaluate $cos \frac{5 π}{3}$ .

Answer

Evaluate Trigonometric Functions

If $sin θ = - \frac{2}{3}$ and θ terminates in quadrant IV, find tan θ.

Solution

One method to solve this problem is to sketch a right triangle in the specified quadrant with an acute angle at the origin and right angle on the x-axis. The sides of the triangle are from the given trigonometric function. Since $sin θ = \frac{y}{r} = - \frac{2}{3}$ . The r is always positive so r = 3 and y = −2. By using the Pythagorean Theorem, find x.

$\begin{array}{l} x^{2} + y^{2} = r^{2} \\ x^{2} + {(- 2)}^{2} = 3^{2} \\ x = \pm \sqrt{5} \end{array}$

Since the triangle is in quadrant IV, the x value is positive and $x = \sqrt{5}$

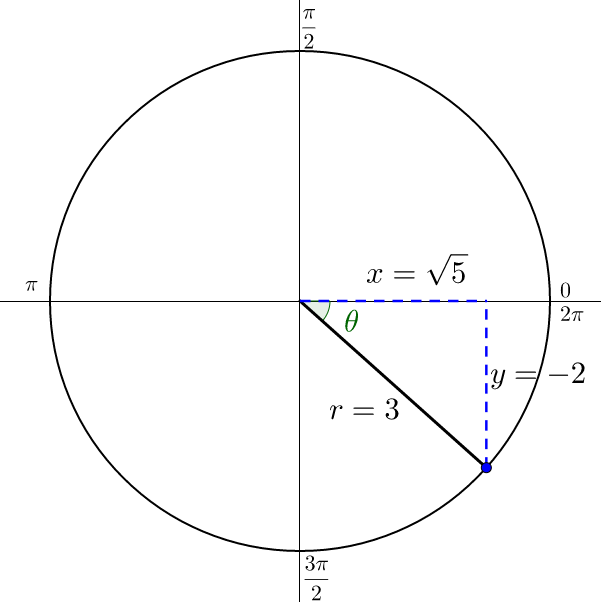
Now evaluate tan θ using the right triangle.

$tan θ = \frac{y}{x} = \frac{- 2}{\sqrt{5}} = - \frac{2 \sqrt{5}}{5}$

If tan α = −2 and α terminates in quadrant II, find sin α.

Answer

$\frac{2 \sqrt{5}}{5}$

Lesson Summary

Trigonometric Functions of Any Angle

$sin θ = \frac{y}{r}$	$csc θ = \frac{r}{y}$
$cos θ = \frac{x}{r}$	$sec θ = \frac{r}{x}$
$tan θ = \frac{y}{x}$	$cot θ = \frac{x}{y}$

where θ is an angle in standard position with point (x, y) on the terminal side and $r = \sqrt{x^{2} + y^{2}}$

Reference Angles

To find the reference angle

Determine the measure of the angle whose terminal side is on the x-axis nearest the terminal side of the given angle.
Subtract the measures of the given angle and the x-axis angle.

Evaluate Trigonometric Functions of Any Real Number

Consider the number to be an angle, θ.
If θ is not between 0 and 2π, find a coterminal angle between 0 and 2π by adding or subtracting 2π.
Find the reference angle.
Evaluate the trigonometric function of the reference angle using special right triangles (lesson 4-04) or the unit circle (lesson 4-02).
Apply a negative sign as needed based on the quadrant θ is in.

Helpful videos about this lesson.

Mr. Wright Teaches the Lesson (https://youtu.be/CfI9hnf0n1M)
Trigonometric Functions Using Reference Angles (http://openstaxcollege.org/l/trigrefang)

Practice Exercises

Evaluate the six trigonometric functions based on the given point on the terminal side of an angle in standard position.
(3, −5)
(−2, −7)
Evaluate the six trigonometric functions of the given angle.
$\frac{π}{2}$
2π
Evaluate the function of θ.
If $sin θ = \frac{1}{5}$ and θ is in quadrant II, find a) cos θ and b) tan θ.
If $sec θ = \frac{4}{3}$ and θ is in quadrant IV, find a) sin θ and b) csc θ.
If $tan θ = - \frac{3}{4}$ and sin θ > 0, find a) cos θ and b) sec θ.
If $cos θ = - \frac{8}{17}$ and tan θ < 0, find a) sin θ and b) cot θ.
Find the reference angle of the given angle.
$\frac{6 π}{5}$
$\frac{4 π}{7}$
$- \frac{8 π}{9}$
$\frac{15 π}{4}$
Evaluate the given trigonometric functions using reference angles.
$sin \frac{3 π}{4}$
$tan \frac{11 π}{6}$
$cos \frac{5 π}{4}$
Mixed Review
(4-04) Let θ be an acute angle. Use the given function value with trigonometric identities to evaluate the given function. If csc θ = 2, find a) cot θ and b) sin θ.
(4-04) A student is standing on the third floor of a building 30 feet above the ground. There are two kids on a lawn playing catch with a Frisbee. The angles of depression from the student in the building to the kids are 45° and 55°. How far apart are the students?
(4-03) Use special right triangles to evaluate a) $sin \frac{π}{3}$ and b) $cot \frac{π}{4}$ .
(4-02) Use the unit circle to evaluate a) $cos \frac{π}{6}$ and b) $tan \frac{7 π}{6}$ .
(4-01) a) Draw the $\frac{17 π}{6}$ in standard position and find a b) positive and c) negative coterminal angle.

Answers

$sin θ = - \frac{5 \sqrt{34}}{34}, cos θ = \frac{3 \sqrt{34}}{34}, tan θ = - \frac{5}{3}, csc θ = - \frac{\sqrt{34}}{5}, sec θ = \frac{\sqrt{34}}{3}, cot θ = - \frac{3}{5}$
$sin θ = - \frac{7 \sqrt{53}}{53}, cos θ = - \frac{2 \sqrt{53}}{53}, tan θ = \frac{7}{2}, csc θ = - \frac{\sqrt{53}}{7}, sec θ = - \frac{\sqrt{53}}{2}, cot θ = \frac{2}{7}$
$sin θ = 1, cos θ = 0, tan θ = undefined, csc θ = 1, sec θ = undefined, cot θ = 0$
$sin θ = 0, cos θ = 1, tan θ = 0, csc θ = undefined, sec θ = 1, cot θ = undefined$
$- \frac{2 \sqrt{6}}{5}$ ; $- \frac{\sqrt{6}}{12}$
$- \frac{\sqrt{7}}{4}$ ; $- \frac{4 \sqrt{7}}{7}$
$- \frac{4}{5}$ ; $- \frac{5}{4}$
$\frac{15}{17}$ ; $- \frac{8}{15}$
$\frac{π}{5}$
$\frac{3 π}{7}$
$\frac{π}{9}$
$\frac{π}{4}$
$\frac{\sqrt{2}}{2}$
$- \frac{\sqrt{3}}{3}$
$- \frac{\sqrt{2}}{2}$
$\sqrt{3}$ ; ½
about 9 ft
$\frac{\sqrt{3}}{2}$ ; 1
$\frac{\sqrt{3}}{2}$ ; $\frac{\sqrt{3}}{3}$
; $\frac{5 π}{6}$ ; $- \frac{7 π}{6}$