Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


Do not judge, or you too will be judged. For in the same way you judge others, you will be judged, and with the measure you use, it will be measured to you. Matthew 7:1-2 NIV

4-08 Inverse Trigonometric Functions

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.3

Snowy Roof
Sloped roof. (pixabay/seablub)

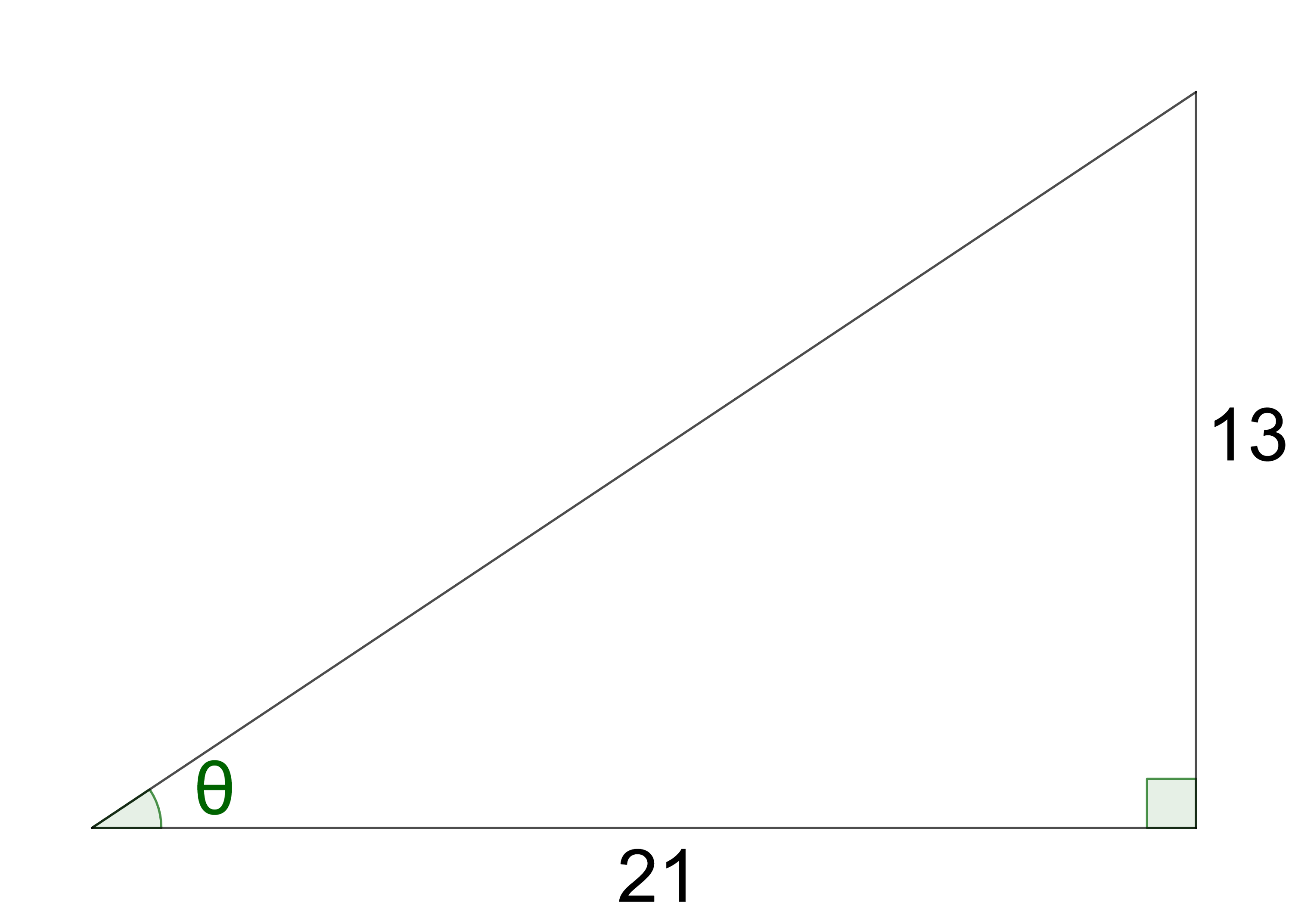
Roofs have to have a certain angle to meet building code in snowy environments. The slope is intended to ensure that rain and snow will slide off the roof. If too much snow sits on the roof, it could collapse under the weight of the snow. Inverse trigonometric functions can be used to calculate the required angle.

Inverse Sine Function

Inverse functions do the opposite of their original function. The input and output of the function are reversed for an inverse function. For example, the domain of the sine function is the angle and the range is the ratio of the coordinates of a point on the unit circle. Inverse sine’s domain is the ratio and the range is the angle. Inverse trigonometric functions are used to find angles.

Graphically, inverse functions are reflections over the line y = x. Take the graph of y = sin x in figure 2a, then reflect it over y = x to form the inverse as in figure 2b. Notice the inverse fails the vertical line test and thus is not a function. Mathematics works better with functions, so limit the inverse sine function to one section as in figure 3.

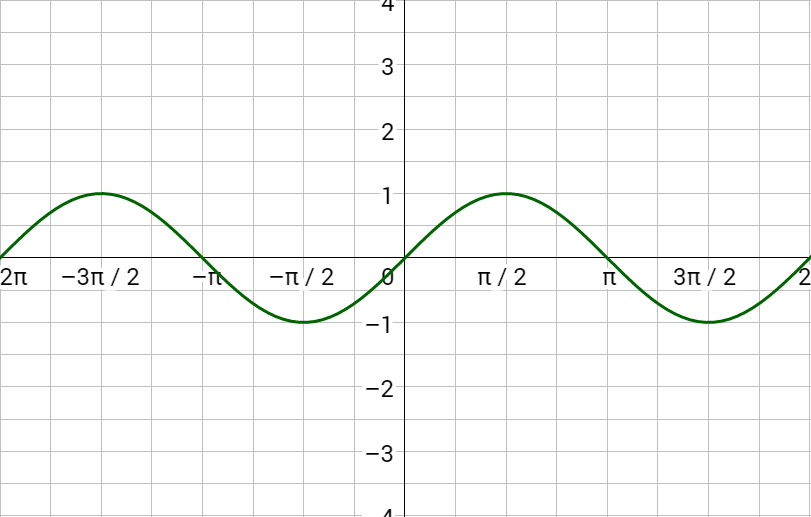
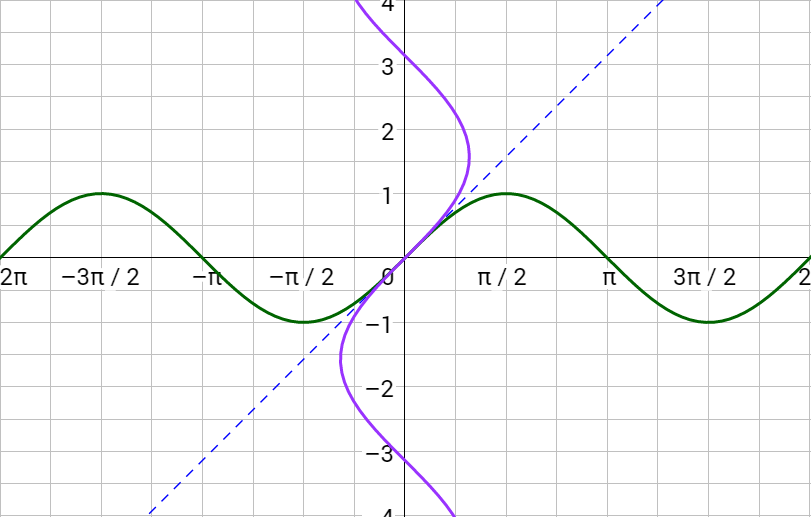
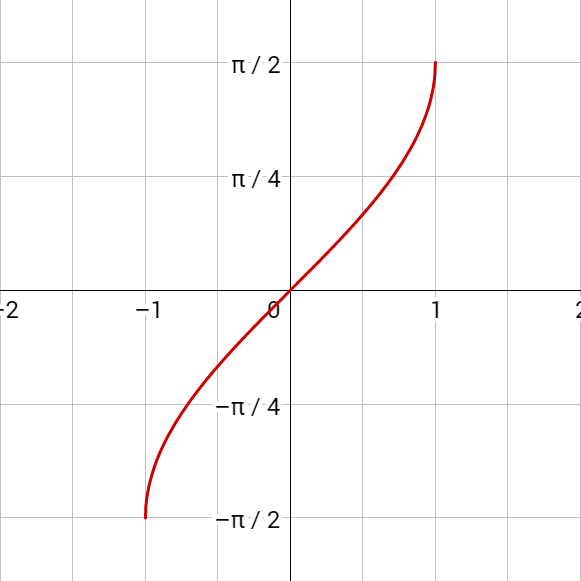
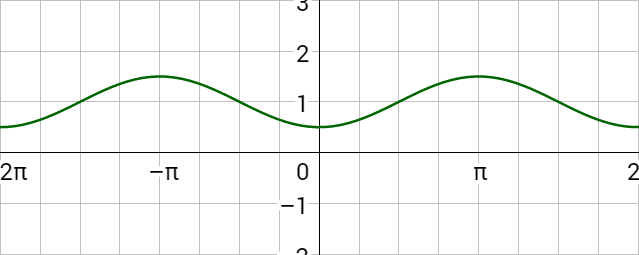
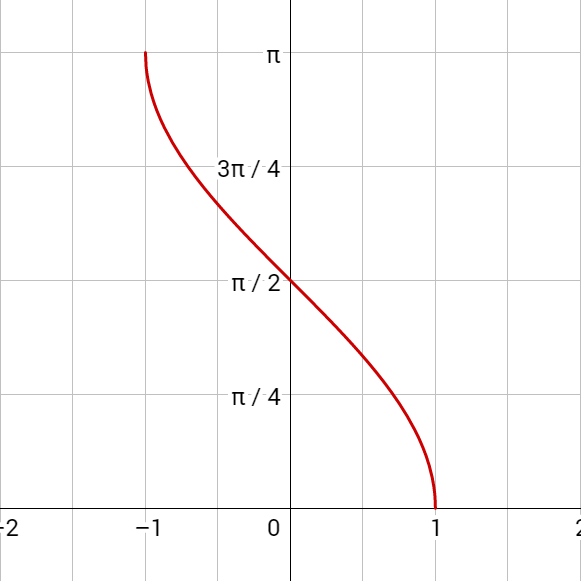
(a) y = sin x; (b) Reflection of y = sin x over y = x.
\(y = \sin^{-1} x\)

Inverse sine is written \(y = \sin^{–1} x\) or \(y = \arcsin x\) where x is the ratio of the coordinates on a circle and y is the angle. The domain is [–1, 1] and the range is \(\left[–\frac{π}{2}, \frac{π}{2}\right]\). To evaluate, find the ratio on the unit circle and read the corresponding angle. Remember the angle must be between \(–\frac{π}{2}\) and \(\frac{π}{2}\).

Range of \(\sin^{–1}\) on the unit circle.

Evaluate Inverse Sine

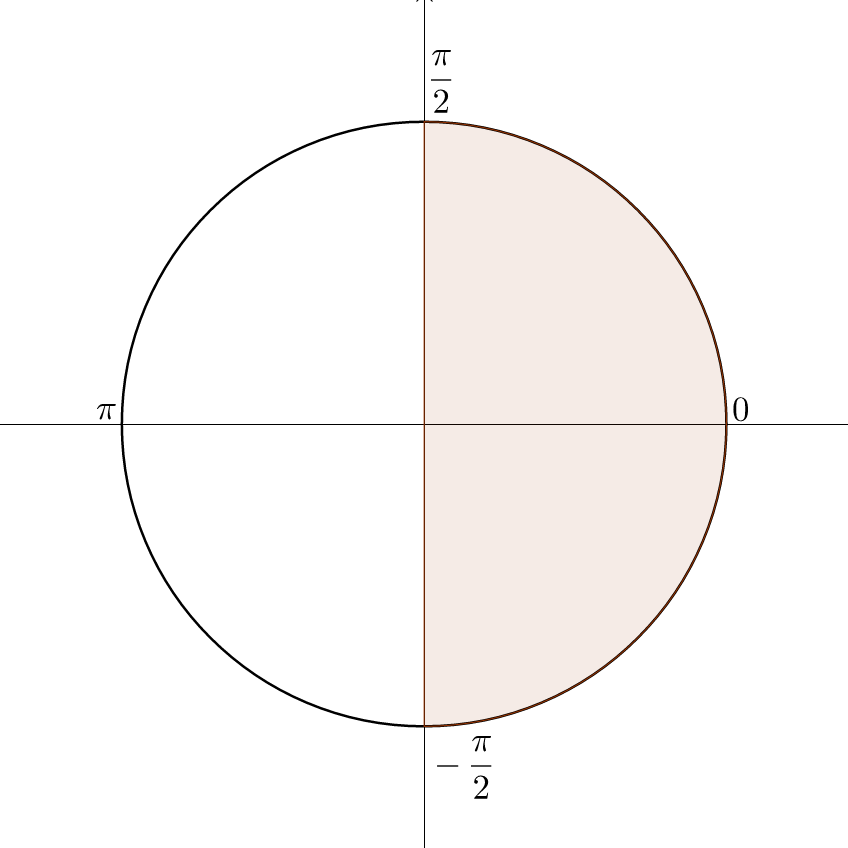
Find the exact value of sin–1 1.

Solution

Find where sin θ = 1 on the unit circle. This occurs at \(\frac{π}{2}\), so \(\sin^{–1} 1 = \frac{π}{2}\).

Find the exact value of \(\arcsin \left(-\frac{\sqrt{2}}{2}\right)\).

Answer

\(–\frac{π}{4}\)

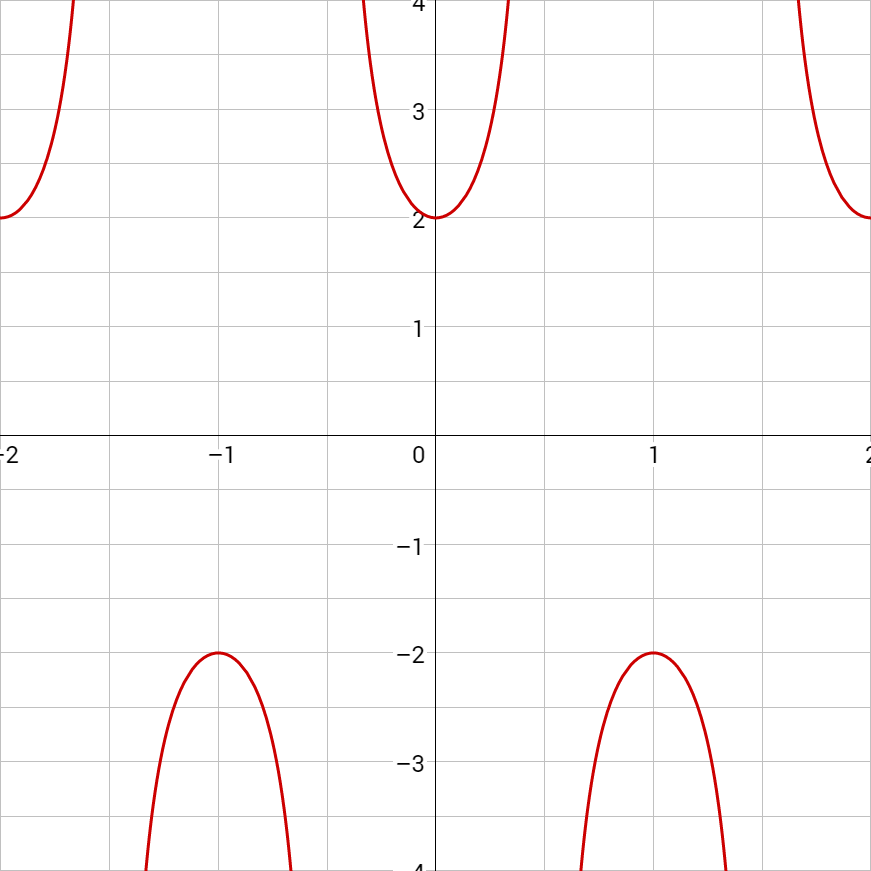
Inverse Cosine and Inverse Tangent

Inverse cosine and tangent are similar in concept to inverse sine. The inverses are used to find the angles. Figure 5 is inverse cosine. The domain is [–1, 1] and the range is [0, π].

\(y = \cos^{–1} x\)

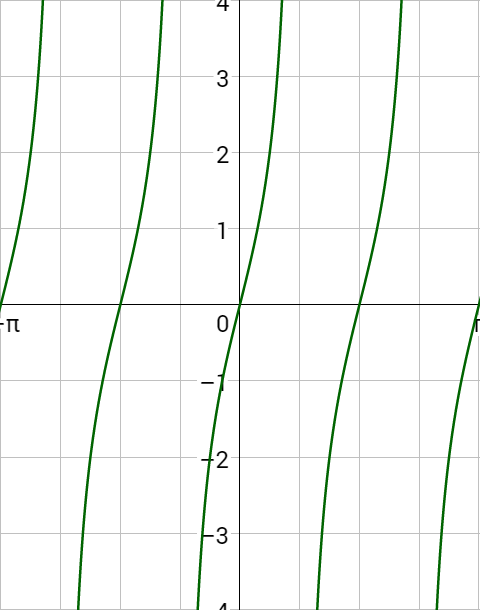
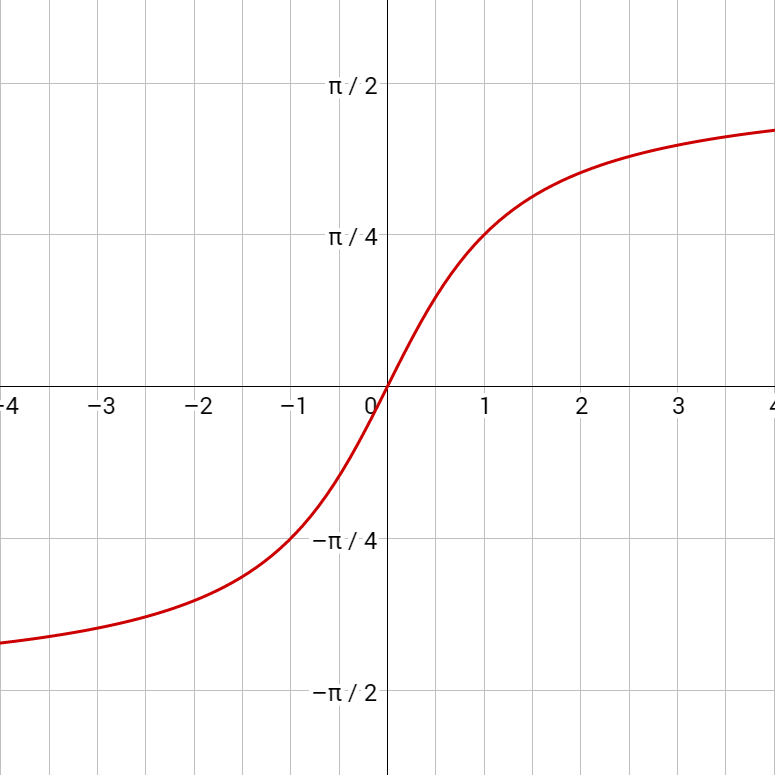
Inverse tangent’s domain is (–∞, ∞) and the range is \(\left(–\frac{π}{2}, \frac{π}{2}\right)\).

\(y = \tan^{–1} x\)
y = sin–1 x

Written: y = sin–1 x or y = arcsin x
Domain: [–1, 1]
Range: \(\left[–\frac{π}{2}, \frac{π}{2}\right]\)

y = cos–1 x

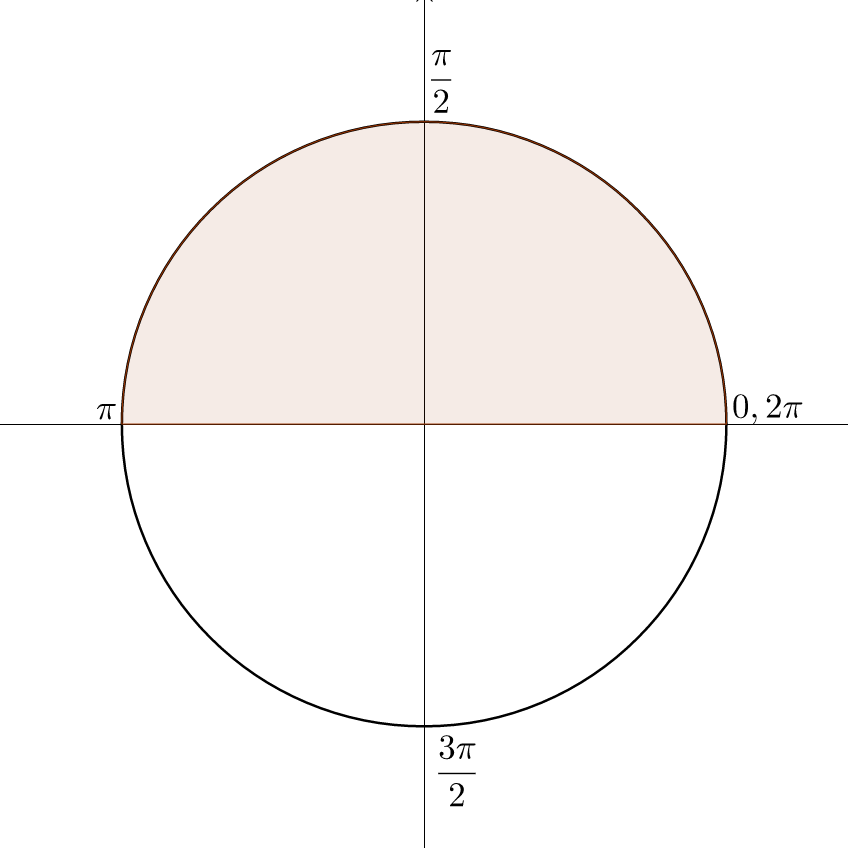
Written: y = cos–1 x or y = arccos x
Domain: [–1, 1]
Range: [0, π]

y = tan–1 x

Written: y = tan–1 x or y = arctan x
Domain: (–∞, ∞)
Range: \(\left(–\frac{π}{2}, \frac{π}{2}\right)\)

Evaluate an Inverse Trigonometric Function

Evaluate a) arccos \(\frac{\sqrt{3}}{2}\) b) cos–1 (–1) c) tan–1 1 and d) arctan (\(–\sqrt{3}\)).

Solution

  1. arccos \(\frac{\sqrt{3}}{2}\): On the unit circle, cosine is the x coordinate. Find a point with the x coordinate of \(\frac{\sqrt{3}}{2}\) with an angle between 0 and π. \(\cos \frac{π}{6} = \frac{\sqrt{3}}{2}\) so \(\arccos \frac{\sqrt{3}}{2} = \frac{π}{6}\).
  2. cos–1 (–1): On the unit circle, cosine is the x coordinate. Find a point with the x coordinate of –1 with an angle between 0 and π. cos π = –1, so cos–1 (−1) = π.
  3. tan–1 1: On the unit circle, tangent is the ratio of \(\frac{y}{x}\). Find a point with the ratio of coordinates is 1 with an angle between \(–\frac{π}{2}\) and \(\frac{π}{2}\). \(\tan \frac{π}{4} = 1\), so \(\tan^{–1} 1 = \frac{π}{4}\).
  4. arctan (\(–\sqrt{3}\)): On the unit circle, tangent is the ratio of \(\frac{y}{x}\). Find a point with the ratio of coordinates is \(–\sqrt{3}\) with an angle between \(–\frac{π}{2}\) and \(\frac{π}{2}\). \(\tan \left(–\frac{π}{3}\right) = –\sqrt{3}\), so \(\arctan \left(–\sqrt{3}\right) = –\frac{π}{3}\).

Find the exact value of a) \(\cos^{–1} \frac{1}{2}\) and b) arctan 0.

Answers

\(\frac{π}{3}\); 0

Evaluate Inverse Trigonometric Functions on a Calculator

When the ratio is not on the unit circle to evaluate inverse trigonometric functions, a calculator will need to be used. On most calculators, the inverse trigonometric functions are the y or S options of the regular trigonometric function keys.

Use a Calculator to Evaluate Trigonometric Functions

Use a calculator to evaluate a) arcsin 0.8660, b) tan–1 (–2.1), and c) arccos (–2) in radians.

Solution

Make sure the calculator is in radian mode (or degree mode is angles in degrees is desired).

  1. On a TI-84, press y ? Ê Ë ª ¸ ¸ Ê ¤ Í. The calculator should display 1.047146746, so sin−1(0.8660) ≈ 1.0471.

    On a NumWorks, press S s 0 . 8 6 6 0 ) X. The display reads arcsin(0.866) = 1.0471.

  2. On a TI-84, press y A Ì Á Ë À ¤ Í. The calculator should display –1.126377117, so tan–1 –2.1 ≈ –1.1264.

    On a NumWorks, press S t - 2 . 1 ) X. the display reads arctan(−2.1) = −1.1264.

  3. On a TI-84, press y @ Ì Á ¤ Í. The display reads "ERR:DOMAIN". This means the input, −2, is not in the domain of cos−1 so there is no output of the function.

    On the NumWorks, press S c - 2 ) X. The calculator should display “nonreal”. That is because –2 is outside of the domain of cos–1, so there is no output of the function.

Use a calculator to evaluate arctan (–0.2) and cos–1 1.

Answers

–0.1974; 0

Lesson Summary
y = sin–1 x

Written: y = sin–1 x or y = arcsin x
Domain: [–1, 1]
Range: \(\left[–\frac{π}{2}, \frac{π}{2}\right]\)

y = cos–1 x

Written: y = cos–1 x or y = arccos x
Domain: [–1, 1]
Range: [0, π]

y = tan–1 x

Written: y = tan–1 x or y = arctan x
Domain: (–∞, ∞)
Range: \(\left(–\frac{π}{2}, \frac{π}{2}\right)\)

Helpful videos about this lesson.

Practice Exercises

  1. Why do f(x) = sin−1 x and g(x) = cos−1 x have different ranges?
  2. Why must the domain of the trigonometric functions be restricted for the inverse trigonometric functions to exist?
  3. Evaluate the expressions.
  4. \(\sin^{−1}\left(−\frac{\sqrt{3}}{2}\right)\)
  5. \(\cos^{−1}\left(−\frac{1}{2}\right)\)
  6. \(\arctan \left(−\sqrt{3}\right)\)
  7. \(\cos^{−1}\left(\frac{\sqrt{3}}{2}\right)\)
  8. Use a calculator to evaluate each expression. Round to the nearest hundredth.
  9. sin−1(−0.3)
  10. arccos(0.6)
  11. tan−1(1.2)
  12. Find the angle θ in the given right triangle. Round to the nearest hundredth.
  14. Mixed Review
  15. (4-07) Sketch two periods of the graph for each of the following functions. Identify the stretching factor, period, and asymptotes.
    \(y = 2\sec\left(πx\right)\)
  16. (4-07) Find an equation for the graph of the function.
  17. (4-06) Determine the amplitude, midline, period, and an equation involving the sine function for the graph.
  18. (4-04) Let θ be an acute angle. Use the given function value with trigonometric identities to evaluate the given function.
    If \(\cos θ = \frac{3}{5}\), find a) sec θ and b) sin θ.
  19. (4-03) Use the special right triangles to evaluate the indicated trigonometric function.
    \(\csc\left(\frac{π}{3}\right)\)

Answers

  1. The function y = sin x is one-to-one on \(\left[−\frac{π}{2}, \frac{π}{2}\right]\); thus, this interval is the range of the inverse function of y = sin x, f(x) = sin−1 x. The function y = cos x is one-to-one on [0, π]; thus, this interval is the range of the inverse function of y = cos x, f(x) = cos−1 x. This also gives each function one positive and one negative quadrant.
  2. In order for any function to have an inverse, the function must be one-to-one and must pass the horizontal line test. The regular sine function is not one-to-one unless its domain is restricted in some way.
  3. \(−\frac{π}{3}\)
  4. \(\frac{2π}{3}\)
  5. \(−\frac{π}{3}\)
  6. \(\frac{π}{6}\)
  7. −0.30
  8. 0.93
  9. 0.88
  10. 0.55 radians
  11. ; a = 2; T = 2; VA: \(x=\frac{1}{2}±n\)
  12. \(y = 2\tan\left(2x\right)\)
  13. \(a=\frac{1}{2}\); midline y = 1; period = 2π; \(y=\frac{1}{2}\sin\left(x-\frac{π}{2}\right)+1\)
  14. 1.667; 0.8
  15. \(\frac{2\sqrt{3}}{3}\)