Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.


…though he may stumble, he will not fall, for the Lord upholds him with his hand. Psalms 37:24 NIV

4-09 Compositions Involving Inverse Trigonometric Functions

Mr. Wright teaches the lesson.

Summary: In this section, you will:

SDA NAD Content Standards (2018): PC.5.3

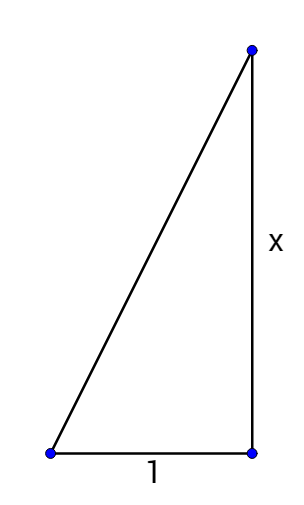
Right triangle
Right triangle with sides x and 1.

Right triangles such as the one in figure 1 can be used to simplify compositions of trigonometric functions such as sin(tan–1 x).

Compositions of Inverse Functions

Lesson 1-09 stated that if f(x) and f–1(x) were inverses, then f(f–1(x)) = x and f–1(f(x)) = x. The same is true for trigonometric functions with an exception. The domain of the inverse functions must be applied.

Composition of Inverse Trigonometric Functions

Remember to be careful that the domain and range of the composition is maintained. Work through the composition from the inside out.

Evaluate Compositions of Inverse Trig Functions

Evaluate a) \(\sin\left(\arcsin \frac{1}{2}\right)\), b) \(\cos\left(\cos^{–1} \frac{2π}{3}\right)\), c) tan(arctan (–10)).

Solution

  1. \(\sin\left(\arcsin \frac{1}{2}\right)\): arcsin is the inner function, and the domain of arcsin is –1 ≤ x ≤ 1. \(\frac{1}{2}\) is in this domain. \(\arcsin\left(\frac{1}{2}\right) = \frac{π}{6}\), then find \(\sin\left(\frac{π}{6}\right) = \frac{1}{2}\). So \(\sin\left(\arcsin \frac{1}{2}\right) = \frac{1}{2}\).
  2. \(\cos\left(\cos^{–1} \frac{2π}{3}\right)\): cos–1 is the inner function, and the domain of cos–1 is –1 ≤ x ≤ 1. \( \frac{2π}{3} \approx 2\), so \(\frac{2π}{3}\) is outside of the domain and thus there is no solution for \(\cos\left(\cos^{–1} \frac{2π}{3}\right)\).
  3. tan(arctan (–10)): arctan is the inner function, and the domain of arctan is any real number. –10 is a real number, so tan(arctan (–10)) = –10.

Evaluate a) sin(sin–1(0.345)) and b) \(\cos\left(\cos^{–1} \left(–\frac{2}{3}\right)\right)\).

Answers

0.345; \(–\frac{2}{3}\)

Evaluate Compositions of Inverse Trig Functions

Evaluate a) \(\arcsin\left(\sin \frac{π}{3}\right)\), b) \(\arccos\left(\cos \frac{5π}{4}\right)\), and c) tan–1(tan π).

Solution

  1. \(\arcsin\left(\sin \frac{π}{3}\right)\): Work from the inside out. \(\sin \frac{π}{3} = \frac{\sqrt{3}}{2}\) so

    \(\arcsin\left(\sin \frac{π}{3}\right)\)
    \(= \arcsin \frac{\sqrt{3}}{2}\)
    \(= \frac{π}{3}\)

  2. \(\arccos\left(\cos \frac{5π}{4}\right)\): \(\cos \frac{5π}{4} = –\frac{\sqrt{2}}{2}\) so

    \(\arccos\left(\cos \frac{5π}{4}\right)\)
    \(= \arccos \left(–\frac{\sqrt{2}}{2}\right)\)
    \(= \frac{3π}{4}\)

    (Remember the range of arccos is 0 ≤ y ≤ π.)

  3. tan–1(tan π): tan π = 0 so

    tan–1(tan π)
    = tan–1(0)
    = 0

    (Remember the range of tan–1 is \(–\frac{π}{2}\) ≤ y ≤ \(\frac{π}{2}\).)

Evaluate a) \(\arctan\left(\tan \frac{3π}{4}\right)\) and b) sin–1(sin(–0.354)).

Answers

\(–\frac{π}{4}\); –0.354

Compositions of trigonometric functions can also be solved using right triangles. Use the inner function to draw a right triangle, then use the triangle to evaluate the outer function.

Use a Right Triangle to Solve Composition of Trigonometric Functions
  1. Draw a right triangle to represent the inner function. Two sides should be labeled.
  2. Use the Pythagorean Theorem to solve for the other side.
  3. Use the triangle to evaluate the outer trigonometric function.

Evaluate a Mixed Composition of Trig Functions

Evaluate a) \(\cos\left(\arcsin \frac{3}{5}\right)\) and b) \(\tan\left(\cos^{–1} \left(–\frac{2}{3}\right)\right)\).

Solutions

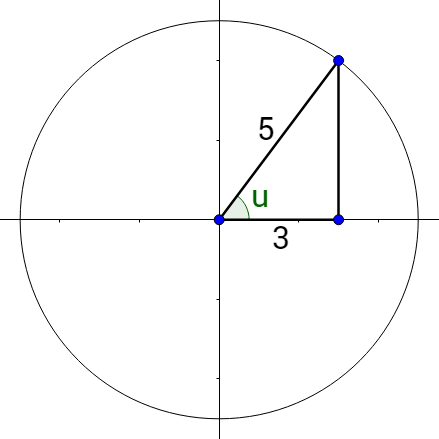
  1. Start with the inner function, \(\arcsin \frac{3}{5}\). \(\sin x = \frac{opposite}{hypotenuse}\), so draw a right triangle in quadrant 1 and label the acute angle by the origin. The opposite side is 3 and the hypotenuse is 5. See figure 2. Use the Pythagorean theorem to find the other side.

    32 + b2 = 52
    b = 4

    Now evaluate the outer function, cos u.

    \(\cos u = \frac{adj}{hyp}\)
    \(\cos u = \frac{4}{5}\)

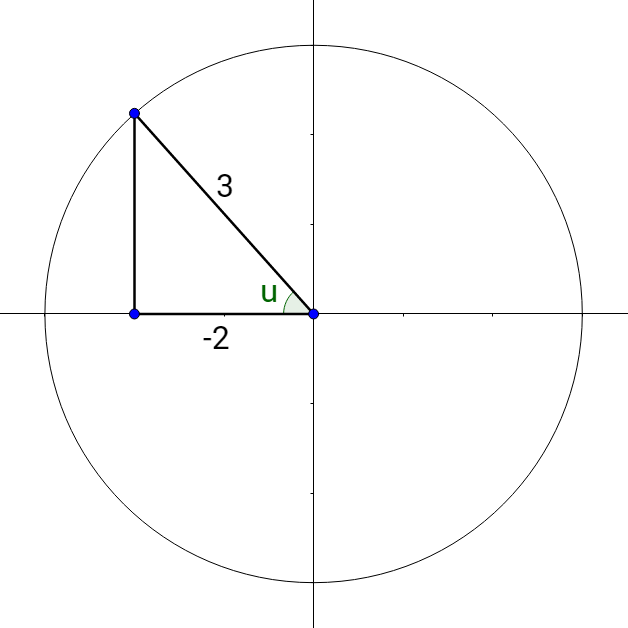
  2. Start with the inner function, \(\cos^{–1} \left(–\frac{2}{3}\right)\) and draw a right triangle. Since the ratio of sides is negative, draw the triangle in the negative quadrant of the inverse trigonometric function. For cos–1 the negative quadrant is quadrant 2. Label the angle by the origin and the adjacent side –2 and hypotenuse 3. See figure 3. Use the Pythagorean theorem to find the other side.

    (–2)2 + b2 = 32
    \(b = \sqrt{5}\)

    Now evaluate the outer function, tan u.

    \(\tan u = \frac{opp}{adj}\)
    \(\tan u = –\frac{\sqrt{5}}{2}\)

Evaluate \(\sin\left(\arctan \left(–\frac{12}{5}\right)\right)\).

Answer

\(–\frac{12}{13}\)

Composition of Trigonometric Functions

Evaluate a) \(\tan^{-1} \left(\cos \left(\frac{3π}{2}\right)\right)\) and b) \(\cos^{-1} \left(\sin \left(\frac{2π}{3} \right)\right)\).

Solutions

  1. Start with the inner function, \(\cos \left(\frac{3π}{2}\right)\). This time the input is an angle, so sketch that on the unit circle. Since it is a quadrantal angle, find a point on the terminal side such as (0, −1). See figure 4.

    $$ \cos u = x $$

    $$ \cos\left(\frac{3π}{2}\right) = 0 $$

    Now evaluate the outer function, inverse tangent.

    $$ \tan^{-1} \frac{y}{x} = u $$

    $$ \tan^{-1} \frac{0}{1} = 0 $$

  2. Start with the inner function, \(\sin \left(\frac{2π}{3}\right)\). This time the input is an angle, so sketch that on the unit circle. Make note of the coordinate of the terminal side, \(\left(-\frac{1}{2}, \frac{\sqrt{3}}{2}\right)\). See figure 5.

    $$ \sin u = y $$

    $$ \sin\left(\frac{2π}{3}\right) = \frac{\sqrt{3}}{2} $$

    Now evaluate the outer function, inverse cosine.

    $$ \cos^{-1} x = u $$

    $$ \cos^{-1} \frac{\sqrt{3}}{2} = \frac{π}{6} $$

Evaluate \(\arccos \left(\sin \left(\frac{π}{4}\right)\right)\).

Answer

\(\frac{π}{4}\)

Composition of Trigonometric Functions Using x

Rewrite as an algebraic expression a) sin(arccos(x)) and b) tan(sin–1(2x)).

Solutions

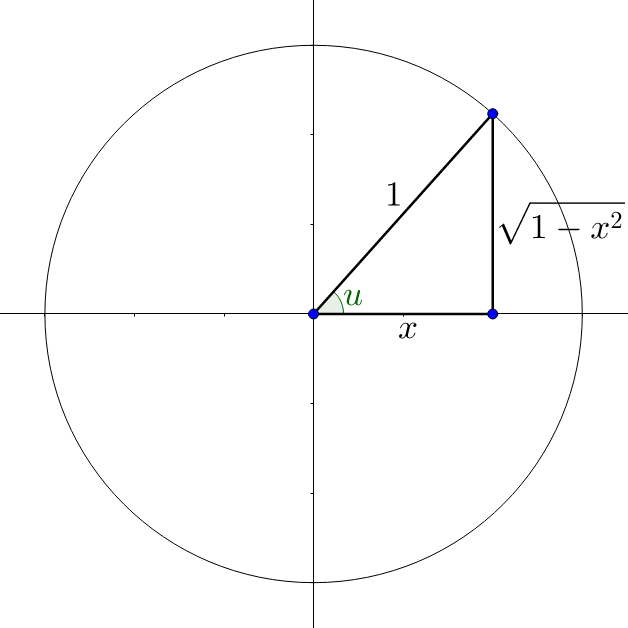
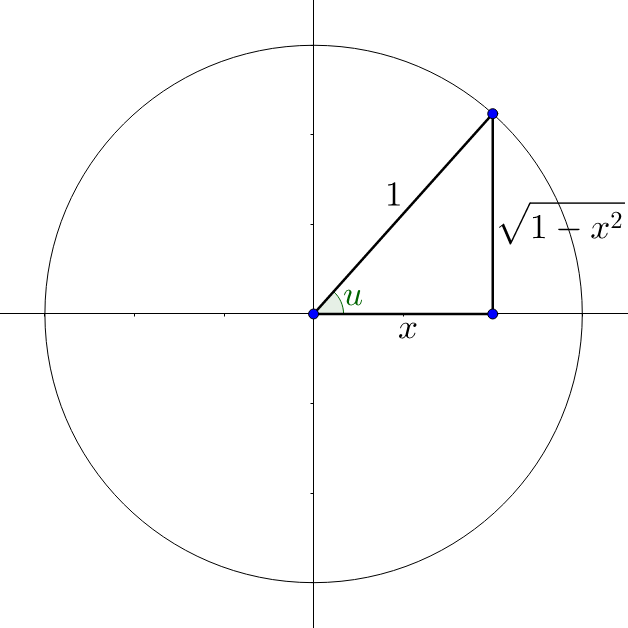
  1. Draw a right triangle and label the sides. The ratio of the sides is \(x = \frac{x}{1}\). Since the inner function is \(\arccos\left(\frac{x}{1}\right)\), the adjacent side is x and the hypotenuse is 1. See figure 6. Use the Pythagorean theorem to find an expression for the third side.

    x2 + b2 = 12
    b2 = 1 – x2
    \(b = \sqrt{1 – x^{2}}\)

    Now evaluate the outer function, sine.

    \(\sin u = \frac{opp}{hyp} = \frac{\sqrt{1 – x^{2}}}{1}\)
    \(\sin u = \sqrt{1 – x^{2}}\)

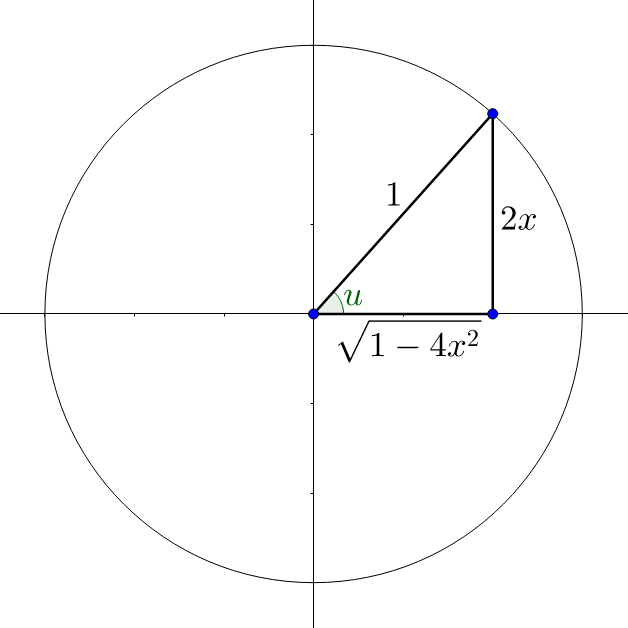
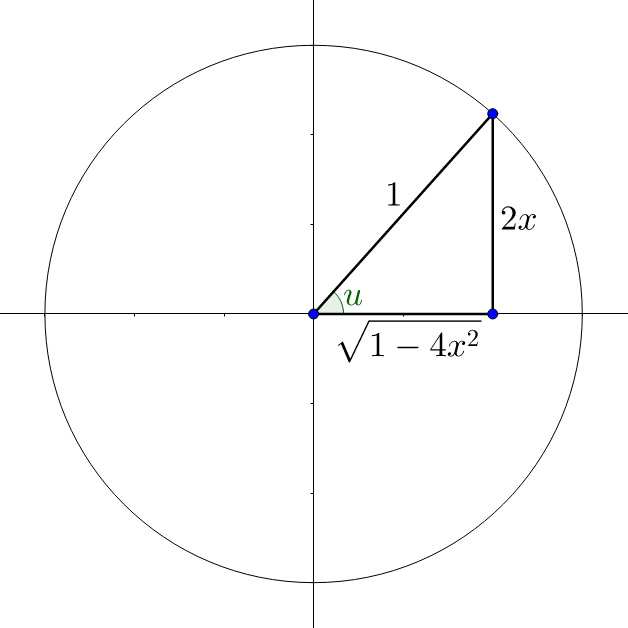
  2. Draw a right triangle and label the sides. The ratio of the sides is \(2x = \frac{2x}{1}\). Since the inner function is \(\sin^{–1}\left(\frac{2x}{1}\right)\), the opposite side is 2x and the hypotenuse is 1. See figure 7. Use the Pythagorean theorem to find an expression for the third side.

    a2 + (2x)2 = 12
    a2 + 4x2 = 1
    a2 = 1 – 4x2
    \(a = \sqrt{1 – 4x^{2}}\)

    Now evaluate the outer function, tangent.

    \(\tan u = \frac{opp}{adj}\)
    \(\tan u = \frac{2x}{\sqrt{1 – 4x^{2}}}\)

Rewrite as an algebraic expression: \(\cos\left(\arctan\left(\frac{x}{2}\right)\right)\).

Answer

\(\frac{2}{\sqrt{x^{2} + 4}}\)

Lesson Summary
Composition of Inverse Trigonometric Functions

Remember to be careful that the domain and range of the composition is maintained. Work through the composition from the inside out.

Using a Right Triangle to Solve Composition of Trigonometric Functions
  1. Draw a right triangle to represent the inner function. Two sides should be labeled.
  2. Use the Pythagorean Theorem to solve for the other side.
  3. Use the triangle to evaluate the outer trigonometric function.

Helpful videos about this lesson.

Practice Exercises (*Optional)

  1. Find the exact value, if possible, without a calculator. If it is not possible, explain why.
  2. \(\tan^{-1}\left(\cos\left(\frac{π}{3}\right)\right)\)
  3. \(\tan^{−1}\left(\sin\left(\frac{π}{2}\right)\right)\)
  4. sin−1(tan(π))
  5. \(\cos^{−1}\left(\sin\left(\frac{2π}{3}\right)\right)\)
  6. \(\cos\left(\tan^{−1}\left(\frac{\sqrt{3}}{3}\right)\right)\)
  7. \(\tan\left(\sin^{−1}\left(\frac{1}{2}\right)\right)\)
  8. Find the exact value of the expression in terms of x with the help of a reference triangle.
  9. tan(cos−1(x + 1))
  10. \(\cos\left(\sin^{−1}\left(\frac{1}{x}\right)\right)\)
  11. sin(tan−1(x − 2))
  12. For what value of x does sin x = sin−1 x? Use a graphing calculator to approximate the answer.
  13. Mixed Review
  14. (4-08) Evaluate \(\arctan\left(\frac{\sqrt{3}}{3}\right)\).
  15. (4-08) Evaluate sin–1 1.
  16. (4-05) If \(\sin θ = \frac{2}{3}\) and tan θ < 0, find a) cos θ and b) cot θ.
  17. *(4-03) Evaluate the six trigonometric functions for the indicated angles.
  18. (3-04) Solve 2x + 2 = 64.
  19. (2-09) Solve 2x2 + 3x + 1 > 0.

Answers

  1. 0.46
  2. \(\frac{π}{4}\)
  3. 0
  4. \(\frac{π}{6}\)
  5. \(\frac{\sqrt{3}}{2}\)
  6. \(\frac{\sqrt{3}}{3}\)
  7. \(\frac{\sqrt{-x^2-2x}}{x + 1}\)
  8. \(\frac{\sqrt{x^2−1}}{x}\)
  9. \(\frac{x-2}{\sqrt{x^2-4x+5}}\)
  10. x = 0
  11. \(\frac{π}{6}\)
  12. \(\frac{π}{2}\)
  13. \(-\frac{\sqrt{5}}{3}\); \(-\frac{\sqrt{5}}{2}\)
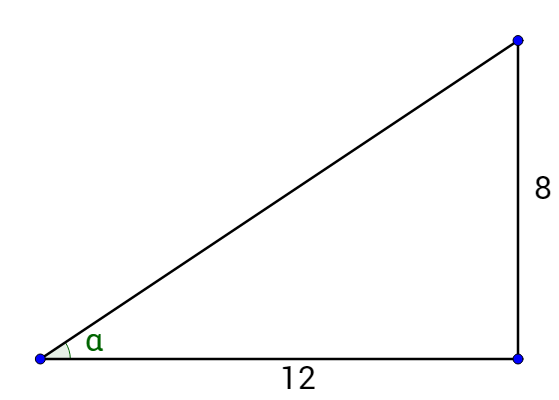
  14. \(\sin α = \frac{2\sqrt{13}}{13}\) \(\cos α = \frac{3\sqrt{13}}{13}\) \(\tan α = \frac{2}{3}\)
    \(\csc α = \frac{\sqrt{13}}{2}\) \(\sec α = \frac{\sqrt{13}}{3}\) \(\cot α = \frac{3}{2}\)
  15. 4
  16. \(\left(−∞, −1\right) ∪ \left(−\frac{1}{2}, ∞\right)\)