Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

At that time people will see the Son of Man coming in clouds with great power and glory. Mark 13:26 NIV

4-10 Applications of Right Triangle Trigonometry

Right triangles can be used to solve many problems. One example is calculating the angle a camera would have to be set at to capture a model rocket at it's apogee, or highest altitude.

Solve Problems with Right Triangles

For problems that can be solved with right triangle trigonometry, draw a triangle as described in the problem. Then use trigonometry to solve for the unknown.

Model Rockets

It is estimated that a certain model rocket will reach an altitude of 200 ft. A photographer is setting up a camera 50 ft away from the launch pad. At what angle should he set the tripod to get a picture at the maximum altitude?

Solution

Draw a right triangle to model the problem.

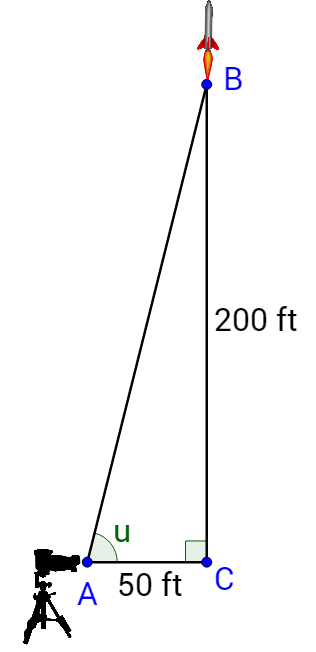
The hypotenuse and the angle with the ground are known. The opposite side is the unknown. Use sine to solve the problem.

\(\tan u = \frac{opp}{adj}\)
\(\tan u = \frac{200 \textrm{ ft}}{50 \textrm{ ft}}\)
\(u = \tan^{−1} \left(\frac{200}{50} \right) \approx 76.0°\)

Find an Acute Angle

In areas that get a lot of snow, roofs must be inclined at a certain angle to meet building code. That way the snow will slide off the roof and not crush the house. In one town the incline must be at least 20° above the horizontal. A builder is making a roof with a rise of 4 feet for every 12 feet of run. Will this roof meet building code?

Solution

Draw a right triangle to represent the roof.

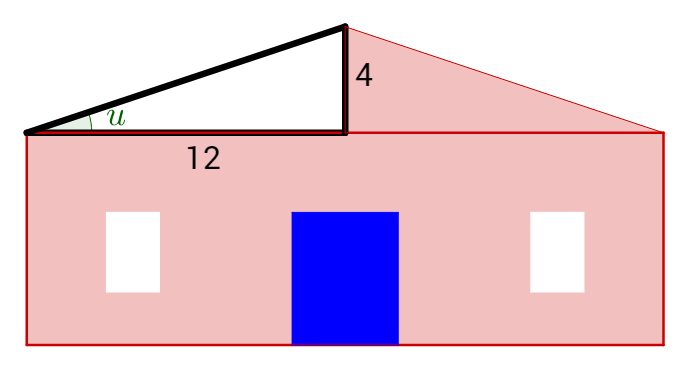
The opposite side is 4 ft and the adjacent side is 12 ft. Tangent has this ratio.

\(\tan u = \frac{4 \textrm{ ft}}{12 \textrm{ ft}}\)
\(u = \tan^{–1} \frac{4}{12} \approx 18.4°\)

This is less than the required 20°, so the roof is not steep enough and will not meet building code.

Solve Right Triangles

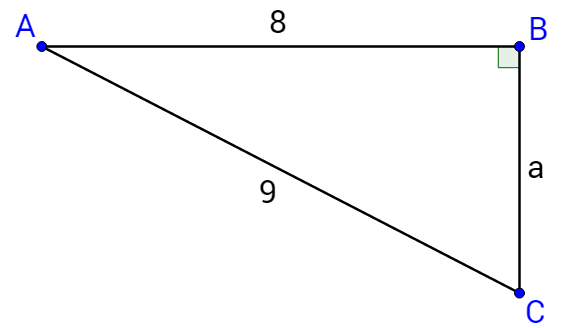
Solving a triangle means to find the measures of all unknown sides and angles. To do this use the trigonometric functions and inverse functions, the Pythagorean theorem, and the triangle sum theorem. The triangle sum theorem states that the sum of the angles of a triangle equal 180°.

Solve a Right Triangle

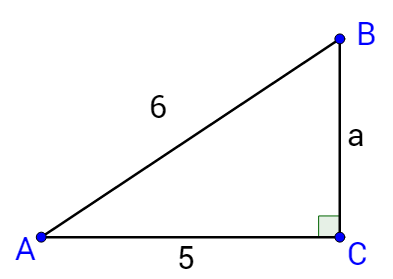
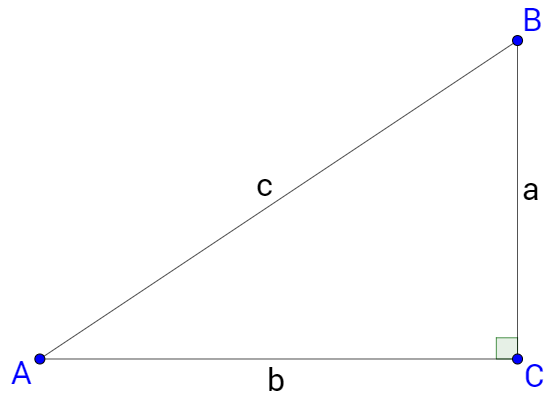
Find the lengths of all the sides and angles using

• Trigonometric functions
• Inverse trigonometric functions
• Pythagorean theorem
• Triangle sum theorem (sum of angle measures = 180°)

The sides are labeled with a lowercase letter to match the opposite angle.

Solve a Right Triangle

Solve the triangle.

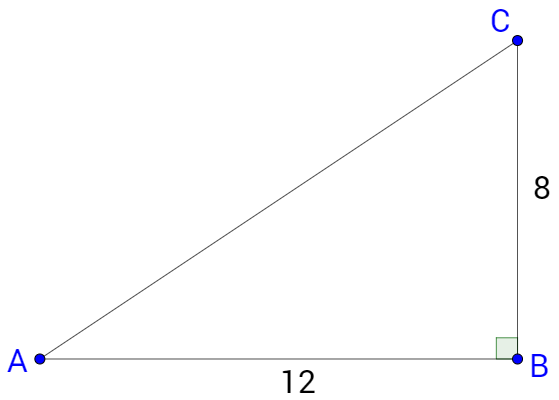
Solution

Since two sides are known, start by finding the third side using the Pythagorean theorem with the hypotenuse, b.

b² = 8² + 12²
b² = 208
\(b = 4\sqrt{13}\)

Now find the angles. Because the side lengths are known, inverse trigonometric functions should be used.

\(A = \tan^{-1} \frac{8}{12}\)
A ≈ 33.7°

Angle C can be found using either inverse tangent or the triangle sum theorem.

A + B + C = 180°
33.7° + 90° + C = 180°
C ≈ 56.3°

Solve the triangle.

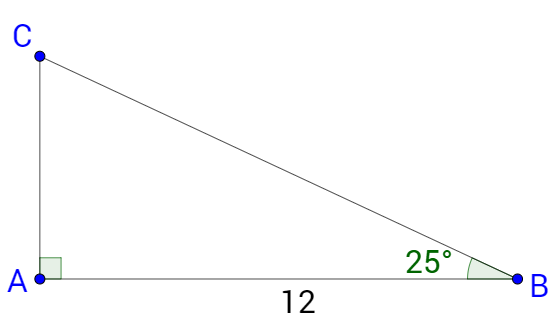
Answer

a ≈ 13.2, b ≈ 5.6, C = 65°

Lesson Summary

---

Solve a Right Triangle

Find the lengths of all the sides and angles using

• Trigonometric functions
• Inverse trigonometric functions
• Pythagorean theorem
• Triangle sum theorem (sum of angle measures = 180°)

The sides are labeled with a lowercase letter to match the opposite angle.

Practice Exercises

1. A 12-foot ladder is leaning against a rain gutter 10 feet above the ground. What angle, in radians, does the ladder make with the ground?
2. Two people climb 220 feet up the side of a sand dune so that the change in elevation is 120 feet. What is the angle of elevation of the side of the sand dune?
3. The congruent legs of an isosceles triangle are 10 cm, and the base is 6 cm. What is the measure of a base angle of the triangle?
4. Without using a calculator, estimate the value of tan⁻¹(1,000,000). Explain your reasoning.
5. A guy-wire is a cable that attaches to the top of an electrical pole at an angle to hold it upright. It forms a right triangle with the pole and the ground. If the pole is 13 feet tall and the guy-wire attaches to the ground 5 feet from the pole, what angle does the wire make with the pole?
6. What is the angle that the line \(y = \frac{2}{3}x\) makes with the positive x-axis?
7. What is the angle that the line \(y = \frac{5}{2}x\) makes with the positive x-axis?
8. The percent grade of a road is the change in height over a 100-foot horizontal distance. What is the percent grade of a road with a 3° angle of elevation?
9. One of the trusses on a railroad bridge is shaped like a right triangle. If the vertical leg is 20 feet and the horizontal leg is 12 feet, what angle does the hypotenuse make with the horizontal leg?
10. Frank is building a chicken coop. The frame for the roof will be an isosceles triangle with a base of 4 feet and a height of 1.5 feet. What angle should he cut the wood at the end of the base to get a tight fit?
11. Solve the Right Triangle

12. 

13. 

14. 

15. 

16. 

17. Mixed Review
18. (4-09) Evaluate \(\sin\left(\cos^{–1} \frac{4}{5}\right)\).
19. (4-09) Evaluate \(\tan^{–1}\left(\tan \frac{π}{3}\right)\).
20. (4-08) Evaluate \(\arcsin \frac{\sqrt{3}}{2}\).
21. (4-07) Graph \(y = \frac{\cos x}{\sin x}\) and y = cot x on the same graph. What is the relationship between the two functions?
22. (4-05) If sec θ = −3 and sin θ < 0, find a) tan θ and b) csc θ.

Answers

1. 0.985
2. 33.1°
3. 72.5°
4. \(\frac{\pi}{2}\)
5. 21.0°
6. 33.7°
7. 68.2°
8. 5%
9. 59.0°
10. 36.9°
11. \(a = \sqrt{11}\), \(A \approx 33.6°\), \(B \approx 56.4°\)
12. \(a = \sqrt{41}\), \(B \approx 51.3°\), \(C \approx 38.7°\)
13. \(c = \sqrt{15}\), \(B \approx 61.0°\), \(C \approx 29.0°\)
14. \(c = \sqrt{65}\), \(A \approx 29.7°\), \(B \approx 60.3°\)
15. \(a = \sqrt{17}\), \(A \approx 27.3°\), \(C \approx 62.7°\)
16. \(\frac{3}{5}\)
17. \(\frac{π}{3}\)
18. \(\frac{π}{3}\)
19. They are the same graph.
20. \(2\sqrt{2}\); \(−\frac{3\sqrt{2}}{4}\)