Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Whoever sows to please their flesh, from the flesh will reap destruction; whoever sows to please the Spirit, from the Spirit will reap eternal life. Galatians 6:8 NIV

4-11 Bearings and Simple Harmonic Motion

The path of a cargo ship can be described using a distance and direction. The direction is called a bearing which can be calculated with trigonometric functions.

Bearings

A direction of such as E 30° N means 30° measured from the east going northward.

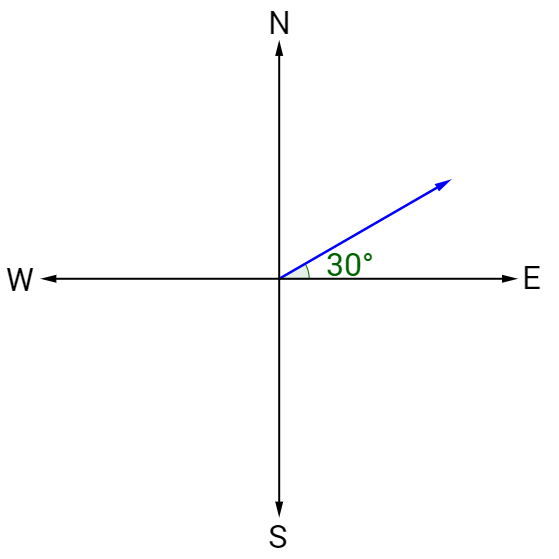
Solve bearing problems by drawing the picture and adding right triangles for each bearing.

Find Bearing Directions

A cargo ship leaves port and heads east at 10 knots (nautical miles per hour) for 1 hour. Then it turns and travels at 15 knots for 0.5 hours at E 40° S. What is the ship's current bearing from port?

Solution

Start by calculating the distances from the speeds and times.

East distance
d = rt
d = (10 knots)(1 hr) = 10 nautical miles

South of east distance
d = rt
d = (15 knots)(0.5 hr) = 7.5 nautical miles

Draw a picture and make right triangles for the bearings.

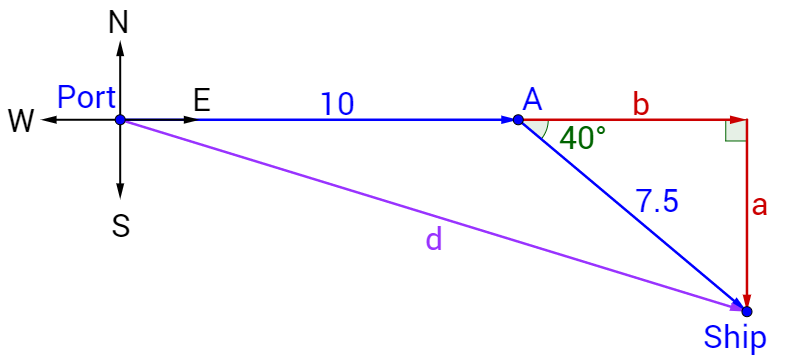
Start by finding the sides of the right triangle.

\(\sin 40° = \frac{a}{7.5\textrm{ mi}}\)
a = 7.5 mi sin 40° ≈ 4.82 mi

\(\cos 40° = \frac{b}{7.5\textrm{ mi}}\)
b = 7.5 mi cos 40° ≈ 5.74 mi

Add the lengths to find the sides of the large right triangle.

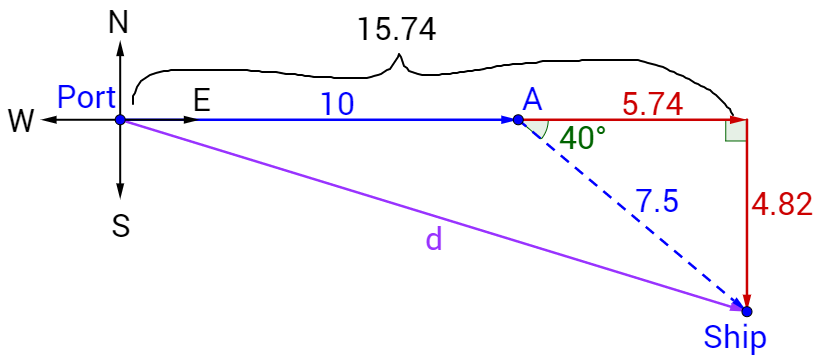
Use the Pythagorean theorem to find the hypotenuse of the triangle which is the distance from the port.

\(d = \sqrt{x^2 + y^2}\)
\(d = \sqrt{\left(15.74\textrm{ mi}\right)^2 + \left(4.82\textrm{ mi}\right)^2} ≈ 16.5\textrm{ mi}\)

Use tangent to find the direction angle.

\(\tan θ = \frac{y}{x}\)
\(\tan θ = \frac{4.82}{15.74}\)
\(θ = \tan^{–1} \frac{4.82}{15.74} ≈ 17.0°\)

The ship is about 16.5 miles at E 17.0° S from port.

Simple Harmonic Motion

Motion that is repeated such as a swinging pendulum can be modeled with sine or cosine. Consider a weight bouncing on the end of a spring. At time t = 0, the weight is in the center equilibrium position, y = 0. A short time later, t = 1, the weight is at the highest point, y = 2. Then at t = 2, the weight is back in the center, y = 0. Next at t = 3, the weight is at the lowest point, y = −2. Finally, at t = 4, the weight is back in the center equilibrium position. See figure 5. It is easy to sketch the sine curve so that it fits the position of the weight.

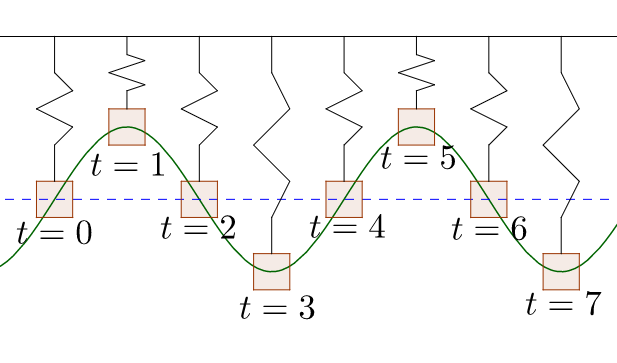
The initial position is y = 0, just like the y-value of sine is 0 at the origin. Remember the transformed sine function from lesson 4-06. The formula was y = a sin(bx – c) + d. a = amplitude, b comes from the period formula \(T = \frac{2π}{b}\), c comes from the phase shift \(PS = \frac{c}{b}\), and d is the vertical shift. This formula is simplified by assuming that there is no phase shift or vertical shift. The formulas for simple harmonic motion are

d = a sin ωt
d = a cos ωt

ω can be found from the period, \(T = \frac{2π}{ω}\), or frequency, \(f = \frac{ω}{2π}\).

Model Simple Harmonic Motion

A weight is bouncing on the end of a spring such that at time t = 0, the weight is at the lowest point, y = 5 cm below equilibrium. After 10 seconds, the weight is back at the lowest point. Write a model for the motion of the weight from equilibrium.

Solution

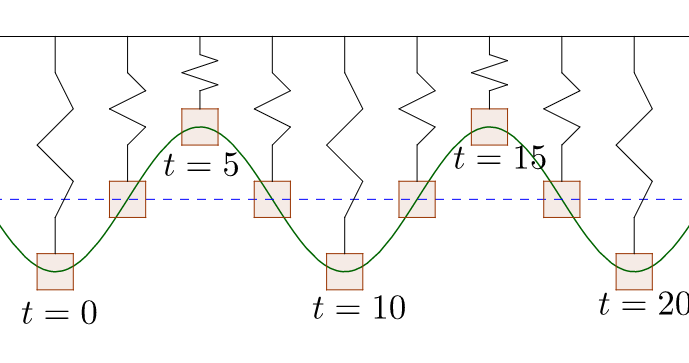
Since the weight starts at a minimum, use cosine. Since it starts at a minimum which is 5 cm below the center equilibrium, a = –5. Because the weight returns to the starting point after 10 seconds, the period is 10. Use it to find ω.

\(T = \frac{2π}{ω}\)
\(10 = \frac{2π}{ω}\)
\(ω = \frac{2π}{10} = \frac{π}{5}\)

Because the weight starts at an minimum or maximum, there is no phase shift so c = 0. Lastly, since the question is asking for motion from equilibrium, there is no vertical shift and d = 0.

The model is \(d = –5 \cos\left(\frac{π}{5}t\right)\)

Practice Exercises

1. Bearings
2. A plane leaves the airport and flies for 1 hour at 130 mph at E 25° N. Then it turns and flies for 2 hours at 110 mph at E 10° S. Finally, it lands. What distance and direction from the airport did the plane land?
3. For exercise, Jim leaves his house and runs at 3.5 mph for 30 min at W 10° N, then he run at 3.1 mph for 45 min at E 80° N where he stops at an ice cream shop. How far away and at what direction is the ice cream shop from Jim's house?
4. A ship leaves port and travels for 2 hours at 3 knots due north. The it changes course to N 10° W for 4 hours. Find the distance and bearing from the starting point.
5. A naturalist studies wolves. One particular wolf has a GPS tracking collar. The naturalist sees that the wolf ran 3 miles at S 20° E and then walked 2 miles due north. Finally, the wolf walked 1 mile at N 45° E. What distance and bearing should the naturalist travel from the wolf's starting point to find the wolf?
6. A safari guide leads his group across the savanna at W 20° S towards a camp 10 km away. Then after traveling 2 km, he discovers he should have been traveling S 20° W. What bearing and distance should he travel to reach camp?
7. Simple Harmonic Motion
8. The displacement of a mass hanging from a spring is modeled by \(h(t) = 3 \cos\left(\frac{8π}{3}t\right)\) where t is in seconds. Find the amplitude, period, and frequency of the displacement.
9. A mass is hanging on a spring and moving with simple harmonic motion. The amplitude is 8 cm, the frequency is 0.5 cycles per second, and it starts at the lowest point. Write a function to model the mass's displacement.
10. A mass suspended by a spring is moving up and down with simple harmonic motion. If the mass is at the highest point, y = 3 cm, at t = 0 and returns to the highest point after 0.50 seconds, write an equation to model the motion.
11. A pendulum is swinging back and forth 5 cm from the center with simple harmonic motion. If the pendulum is at the center point at t = 0 and completes one full swing in 1.5 seconds, write an equation to model the horizontal position of the pendulum.
12. A daredevil bungee jumped off a bridge and is now bouncing up and down with simple harmonic motion. a) If the lowest point at t = 0 is at 10 feet above the water and the highest point at t = 5 s is 50 feet above the water. How high above the water is the equilibrium point? b) What is the amplitude? c) Write an equation modeling the motion from equilibrium. d) Write an equation modeling the motion of the height above the water.
13. Mixed Review
14. (4-10) A meter stick is placed vertically on the ground. If its shadow is 1.3 m long, what is the angle of elevation of the sun?
15. (4-10) Solve the triangle.
    

    

16. (4-09) Find the exact value of the expression in terms of x.
    \(\sin\left(\cos^{−1}\left(\frac{x}{2}\right)\right)\)
17. (4-08) What is the domain and range of a) sin⁻¹, b) cos⁻¹, and c) tan⁻¹?
18. (4-06) Graph two full periods of each function and state the amplitude, period, and midline. State the phase shift and vertical translation, if applicable. Round answers to two decimal places if necessary.
    \(y = −2\sin\left(πx\right) + 3\)

Answers

1. 334.9 miles, at E 2.9° N
2. 2.9 miles at W 63.0° N
3. 17.9 miles at N 6.7° W
4. 1.7 miles at E 3.7° S
5. 8.85 km at W 80.0° S
6. amplitude: 3; period: 3/4; frequency: 4/3
7. y = −8 cos(πt)
8. y = 3 cos(4πt)
9. \(y = 5 \sin\left(\frac{4π}{3}t\right)\)
10. 30 ft; 20 ft; \(y = −20 \cos\left(\frac{π}{5}t\right)\); \(y = −20 \cos\left(\frac{π}{5}t\right)+30\)
11. 37.6°
12. B = 36.87°; a = 8; c = 10
13. \(\frac{\sqrt{4 − x^2}}{2}\)
14. D: [−1, 1] R: \(\left[−\frac{π}{2}, \frac{π}{2}\right]\); D: [−1, 1] R: [0, π]; D: (−∞, ∞); R: \(\left(−\frac{π}{2}, \frac{π}{2}\right)\)

15. 

    ; amplitude: 2; period: 2; midline: y = 3; phase shift: 0; vertical translation: 3