Precalculus by Richard Wright

Previous Lesson Table of Contents Next Lesson

Are you not my student and
has this helped you?

This book is available
to download as an epub.

Then you will call, and the Lord will answer; you will cry for help, and he will say: Here am I. Isaiah 58:9 NIV

8-06 Linear Programming

During WWII, liberty ships ferried war material from the USA to European allies. They were built in large quantities with a simple basic design. Organizers needed a way to optimize how ships were deployed and what was loaded on them. Similar problems requiring maximizing or minimizing encouraged mathematicians to develop a method called linear programming. Linear programming is an optimization strategy to find the maximum or minimum of an objective function based on constraints. The objective function is the function of which the maximum or minimum is desired. The constraints are a system of inequalities that limit the values that can be used in the objective function. Linear programming has been used by the United Kingdom for the selection of ships and transport aircraft to support deployment of their military assets.

Linear Programming

Solve linear programming problems in two variables by graphing the constraints and finding the vertices of the solution area. The maximum or minimum of the objective function will be on one of the vertices, so substitute the vertices into the objective function to determine which point produces the maximum or minimum.

Linear Programming

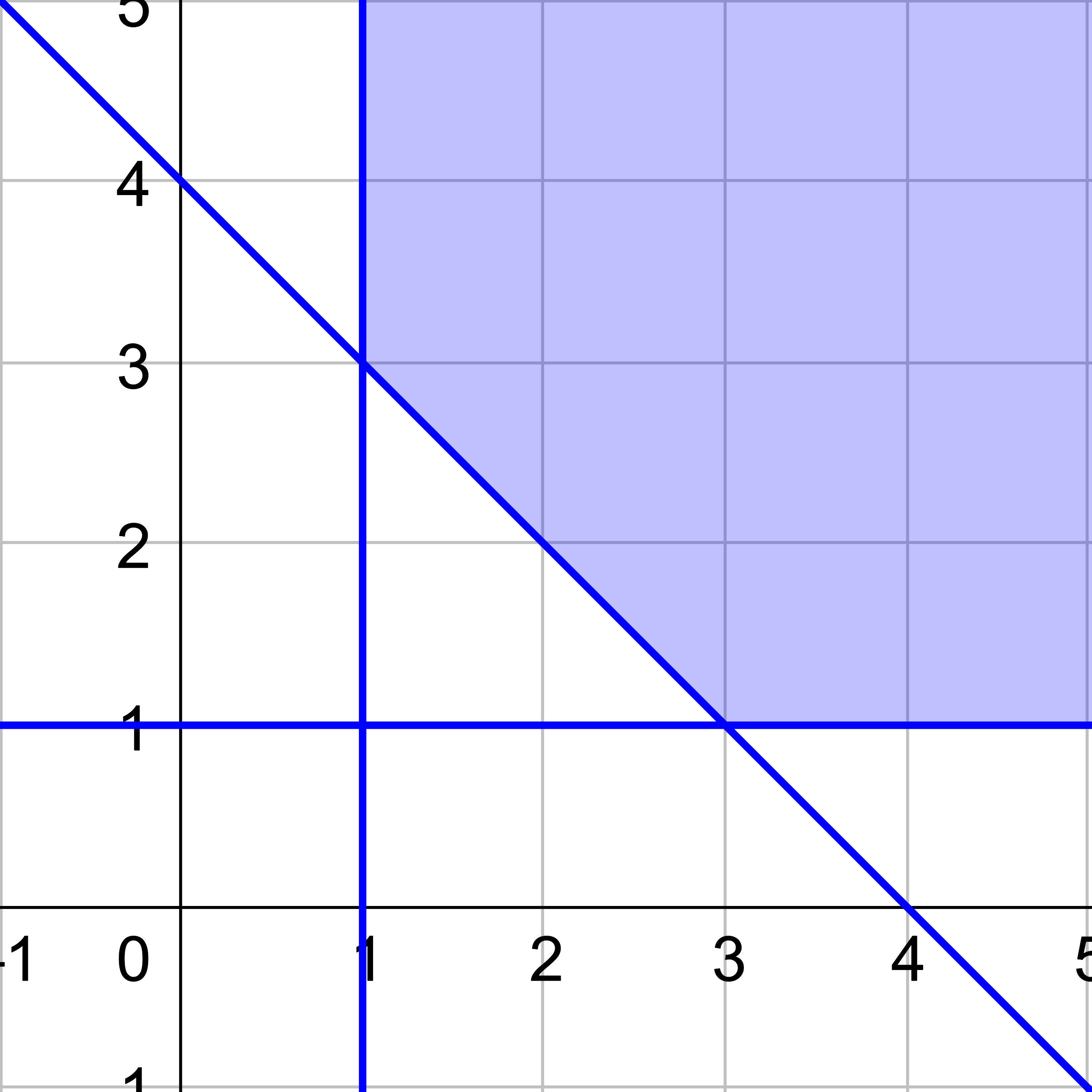
Find the maximum for C = 2x + y given \(\left\{\begin{align} y &≥ \frac{5}{9} x \\ y &≤ 13 \\ x &≤ 9 \\ x &≥ 0 \end{align}\right.\).

Solution

Graph the constraints (the system of inequalities) and find the vertices of the shaded area.

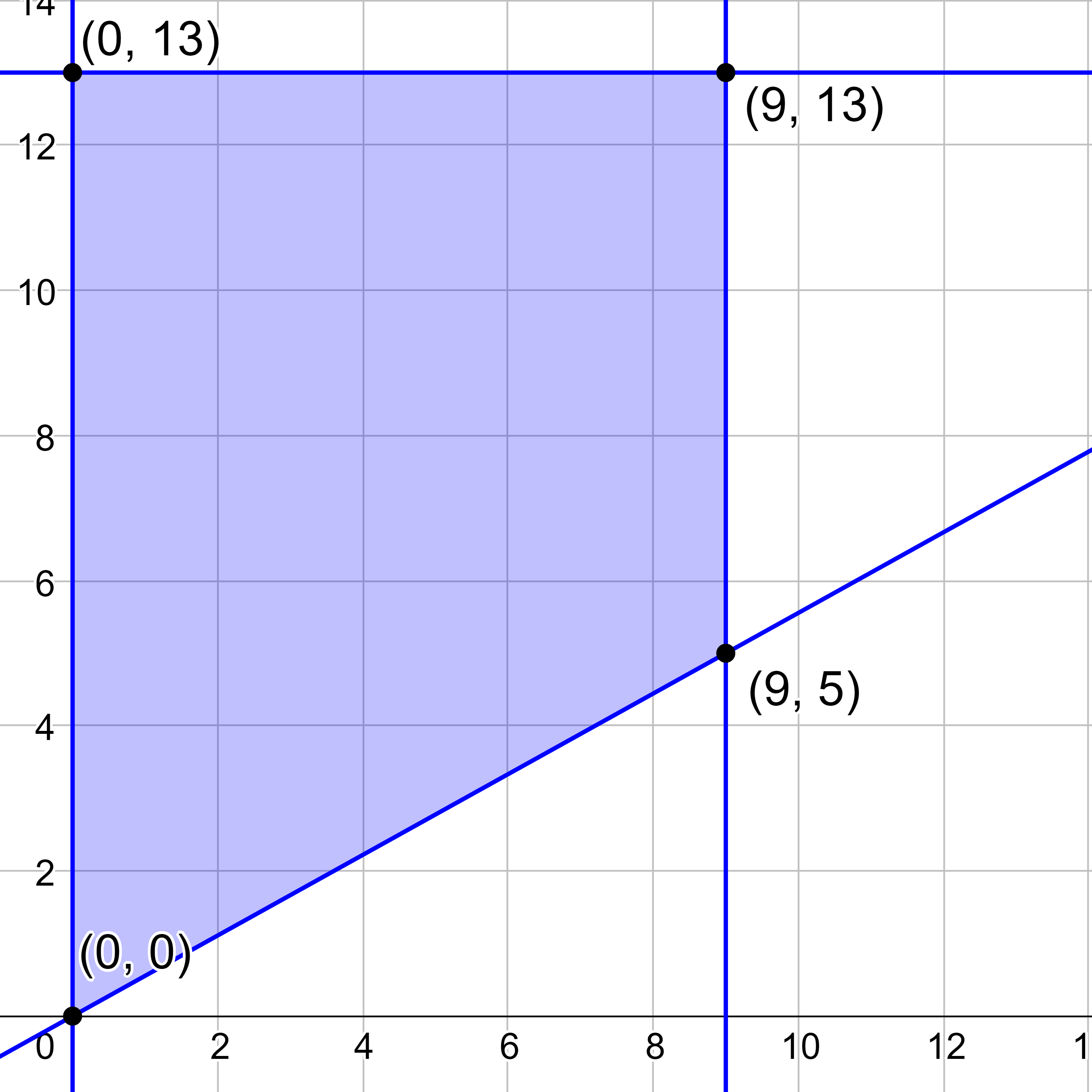
Substitute each vertex into the objective function and find which one produces the maximum.

C = 2x + y

(0, 0): C = 2(0) + (0) = 0

(0, 13): C = 2(0) + 13 = 13

(9, 13): C = 2(9) + 13 = 31

(9, 5): C = 2(9) + 5 = 23

The maximum is 31 and occurs at (9, 13).

Unbounded Constraints

Sometimes the constraints do not form a closed shape. These systems on constraints are called unbounded. In unbounded systems, there can only be a maximum or a minimum, but not both because it is possible to pick points approaching infinity in some direction.

Unbounded Constraints

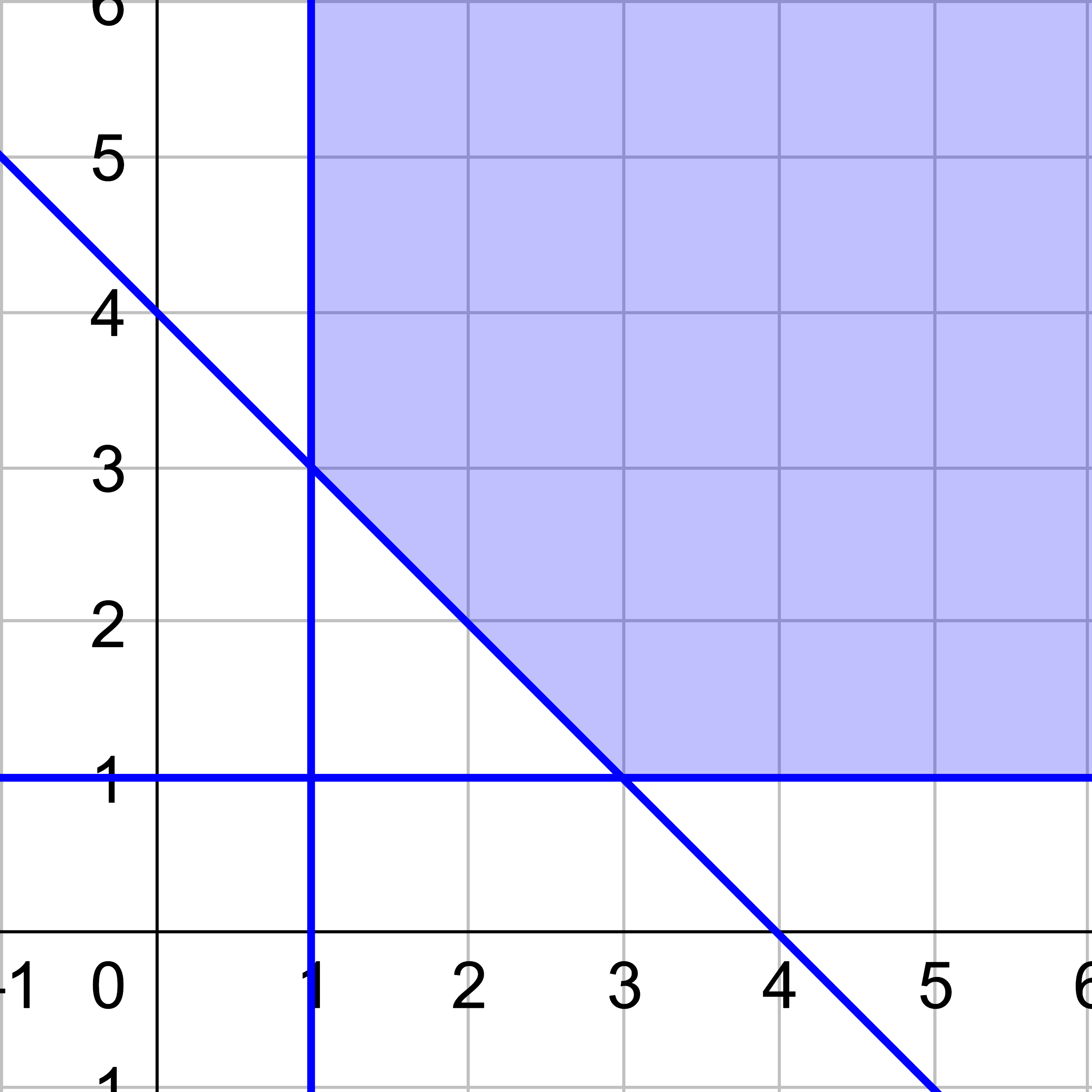
Find the minimum of the objective function C = x + 3y given the constraints:

$$ \left\{\begin{align} y &≥ 0 \\ x &≥ 1 \\ y &≥ -\frac{1}{2} x + 3 \end{align}\right. $$

Solution

Graph the system of inequalities and find the vertices of the shaded area.

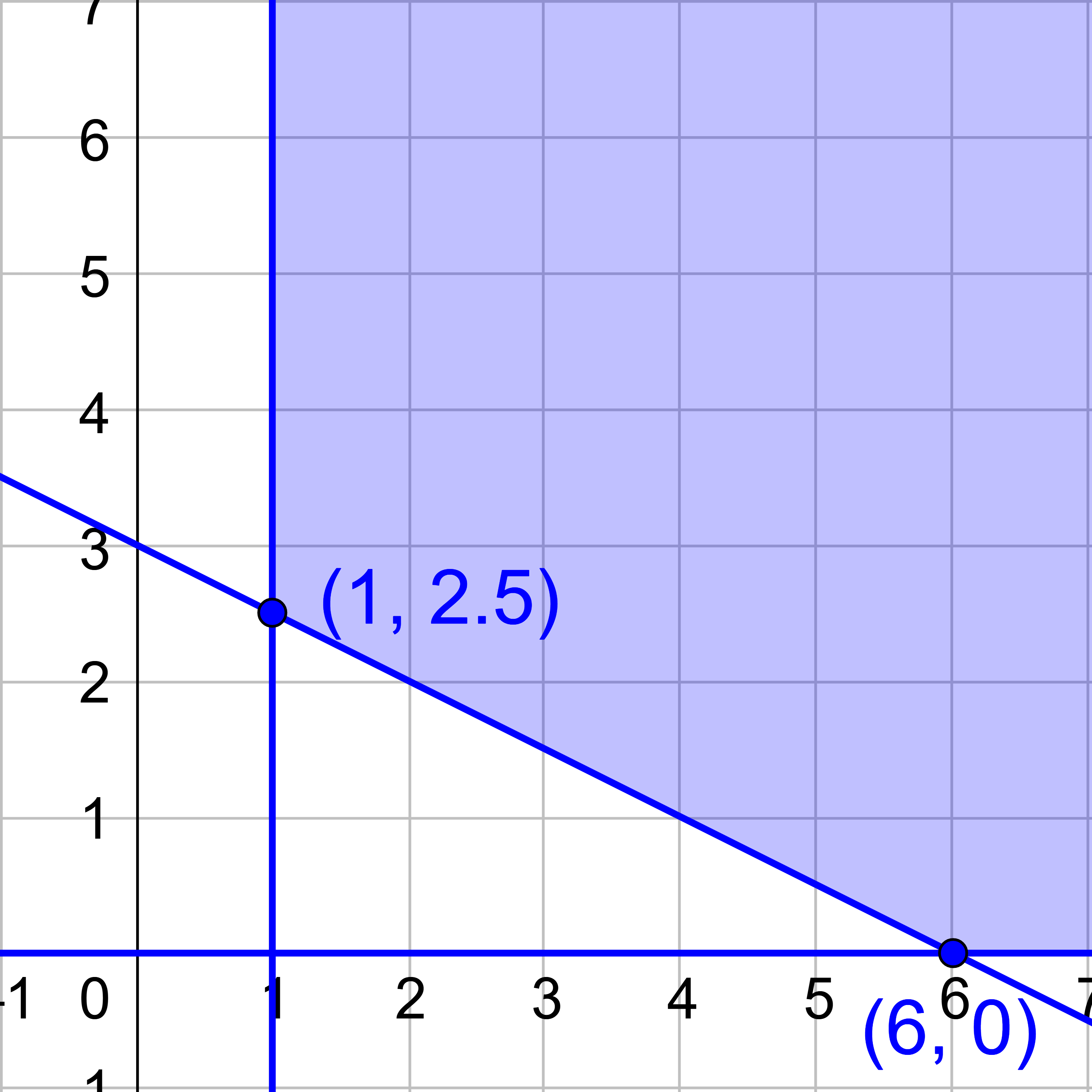
The vertices are (1, 2.5) and (6, 0). Try these in the objective function to find the minimum.

Try (1, 2.5).

C = x + 3y

C = 1 + 3(2.5)

C = 8.5

Try (6, 0).

C = x + 3y

C = 6 + 3(0)

C = 6

The minimum is 6 and occurs at (6, 0).

Real-World Example

A small furniture manufacturer makes ornate chairs and fancy tables. It takes 3 hours to assemble and 1 hour to paint an ornate chair. It takes 2 hours to assemble and 1 hour to paint a fancy table. The factory has 36 man-hours for assembly and 24 man-hours for painting per day. The company makes a profit of $30 per ornate chair and $20 per fancy table. Use linear programming to determine the ideal number of chairs and tables they should produce per day, assuming that they are able to sell everything they produce.

Solution

Organize the constraint information into a table in order to write inequalities.

	Ornate Chair (x)	Fancy Table (y)	Total time available
Assembly	3	2	36
Paint	3	1	24
Profit	$30	$20

Write the constraints based on the table. Include x ≥ 0 and y ≥ 0 to indicate that the factory cannot produce a negative number of chairs and tables.

$$ \left\{\begin{align} 3x + 2y &≤ 36 \\ 3x + y &≤ 24 \\ x &≥ 0 \\ y &≥ 0 \end{align}\right. $$

Graph the constraints the find the vertices.

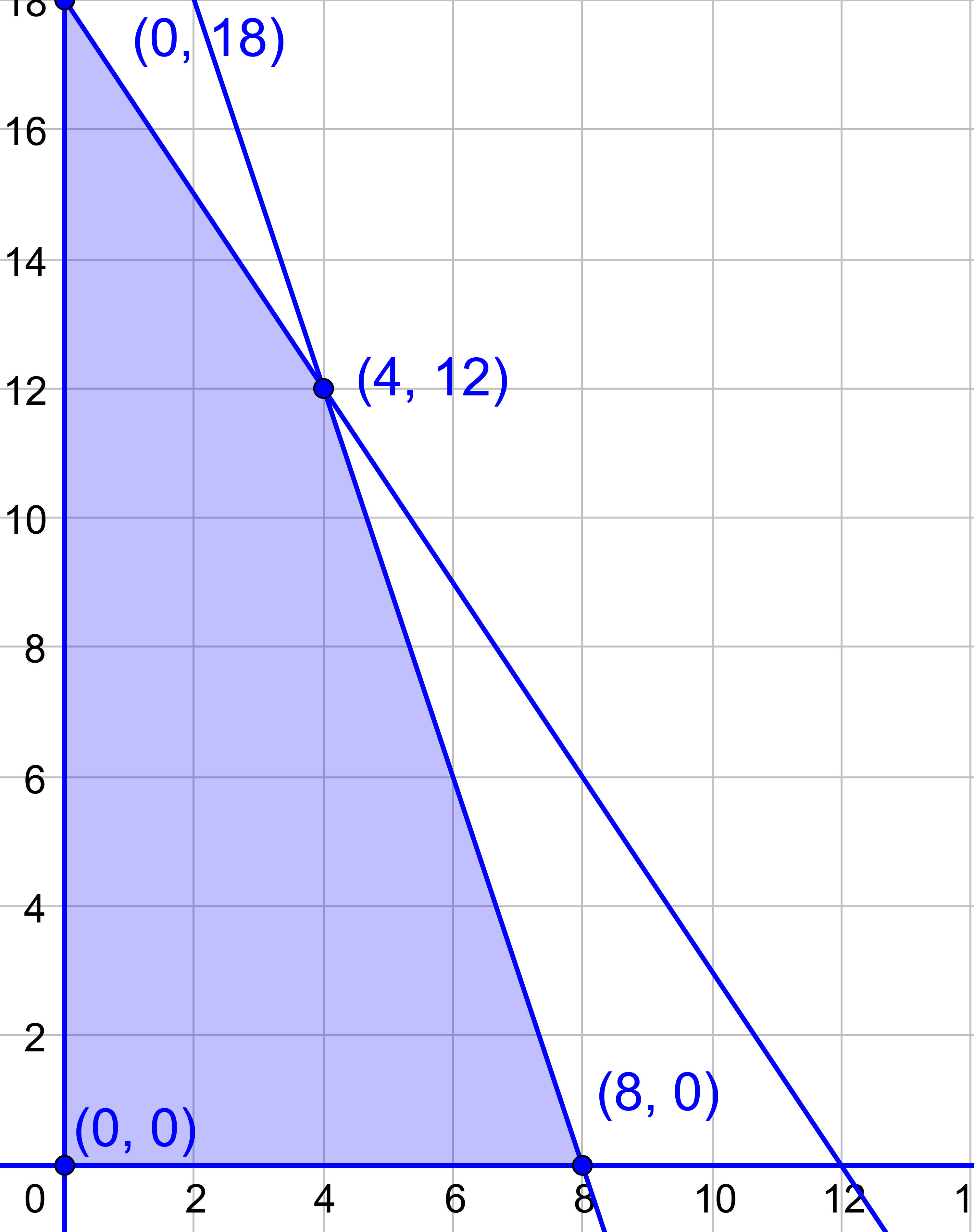
The objective function is the profit. From the table, the profit is P = 30x + 20y. Plug in the vertices to find the maximum profit.

Try (0, 0).

P = 30x + 20y

P = 30(0) + 20(0)

P = 0

That was not surprising because it they make nothing, then they get no profit. Next try (8, 0).

P = 30x + 20y

P = 30(8) + 20(0)

P = 240

Try (4, 12).

P = 30x + 20y

P = 30(4) + 20(12)

P = 360

Try (0, 18).

P = 30x + 20y

P = 30(0) + 20(18)

P = 360

Two vertices gave the same maximum of 360. That means that any point along that line on the side of the shaded area will give 360 when plugged into the objective function. The furniture company then needs to make a decision. They probably should make both chairs and tables so that they do not rely on only one product in case the market changes. Thus, they should produce 4 ornate chairs and 12 fancy tables a day to earn a profit of $360.

Practice Exercises

1. What is meant by unbounded constraints? Draw an example.
2. Use linear programming to find the maximum and minimum (if possible) of the objective function given the constraints.
3. Objective function: \(z = 2x + y\)
   Constraints: \(\left\{\begin{align} x + y &≥ 2 \\ x &≤ 2 \\ y &≤ 2 \end{align}\right.\)
4. Objective function: \(z = y - x\)
   Constraints: \(\left\{\begin{align} 0 &≤ x ≤ 4 \\ y &≥ 1 \\ y &≤ \frac{1}{2}x + 1 \end{align}\right.\)
5. Objective function: \(z = x + 3y\)
   Constraints: \(\left\{\begin{align} 1 &≤ x ≤ 3 \\ 2 &≤ y ≤ 4 \end{align}\right.\)
6. Objective function: \(z = \frac{1}{2}x + y\)
   Constraints: \(\left\{\begin{align} 0 &≤ y ≤ 6 \\ x &≥ 0 \\ y &≥ 2x - 4 \end{align}\right.\)
7. Objective function: \(z = x + 2y\)
   Constraints: \(\left\{\begin{align} 0 &≤ x ≤ 10 \\ 0 &≤ y ≤ 6 \\ y &≤ -x + 15 \end{align}\right.\)
8. Objective function: \(z = \frac{1}{2}x + \frac{1}{3}y\)
   Constraints: \(\left\{\begin{align} x + 2y &≤ 20 \\ 4x + y &≤ 38 \\ x &≥ 0 \end{align}\right.\)
9. Objective function: \(z = x + y\)
   Constraints: \(\left\{\begin{align} x + y &≥ 4 \\ x &≥ 1 \\ y &≥ 2 \end{align}\right.\)
10. Problem Solving
11. You need to buy some filing cabinets for your office storage. You know that Cabinet A costs $20 each, takes 2 ft² of floor space, and holds 4 ft³ of files. Cabinet B costs $60 per unit, takes 1 ft² of floor space, and holds 6 ft³ of files. You have been given a $600 budget. The office only has floor space for 30 ft² of cabinets. How many of each model should you buy, in order to maximize storage volume?
12. A small company makes two different brackets. It takes 5 screws and 2 bolts to make bracket X. And it takes 2 screws and 4 bolts to make bracket Y. The factory has 100 screws and 80 bolts delivered every day. The company makes a profit of $1 per bracket X and $2 per bracket Y. Use linear programming to determine the ideal numbers of each type of bracket they should produce per day, assuming that they are able to sell everything they produce.
13. Mixed Review
14. (8-05) Describe how to graph a system of linear inequalities.
15. (8-04) Find the partial fractions for \(\frac{3x + 2}{x^2 + x}\).
16. (8-03) Solve the system of equations \(\left\{\begin{align} x + 2y + z &= 6 \\ y + z &= 2 \end{align}\right.\)
17. (8-01) Solve by substitution \(\left\{\begin{align} x^2 + y^2 &= 16 \\ x + y &= 0 \end{align}\right.\)
18. (7-07) Convert the polar equation to rectangular: r = 4 cos θ.

Answers

1. The shaded area is not a closed shape;
   

   

2. Max: 6 at (2, 2); Min: 2 at (0, 2)
3. Max: 1 at (0, 1); Min: −3 at (4, 1)
4. Max: 15 at (3, 4); Min: 7 at (1, 2)
5. Max: \(\frac{17}{2}\) at (5, 6); Min: 0 at (0, 0)
6. Max: 21 at (9, 6); Min: 0 at (0, 0)
7. Max: 6 at (8, 6); Min: Does not exist
8. Max: Does not exist; Min: 4 anywhere from (1, 3) to (2, 2)
9. Purchase 12 of cabinet A and 6 of cabinet B
10. Produce 0 of bracket X and 20 of bracket Y (In real life, you might want to still make both brackets for so not to be tied to only one product. In that case producing 15 of bracket X and 12 of bracket Y makes almost the same profit.)
11. Graph each of the inequalities on the same coordinate plane. The solution is the intersection of the shaded areas.
12. \(\frac{2}{x} + \frac{1}{x+1}\)
13. (a + 2, −a + 2, a)
14. \(\left(2\sqrt{2}, -2\sqrt{2}\right), \left(-2\sqrt{2}, 2\sqrt{2}\right)\)
15. x² + y² − 4x = 0